【自然语言处理】— 隐马尔可夫模型
- 【自然语言处理】— 隐马尔可夫模型
- 引例
- 隐马尔可夫模型概念
- 隐马尔可夫模型的关键
- 隐马尔可夫模型的数学表示
- 隐含状态与观测结果
- 状态转移矩阵
- 观测概率矩阵
- 初始状态概率向量
- 小结
【自然语言处理】— 隐马尔可夫模型
引例
假设有三种不同的骰子,分别是立方体,正四面体,正八面体,分别有1-6,1-4,1-8,分别记作D6、D4、D8。每个面出现的概率分别是1/6,1/4,1/8。
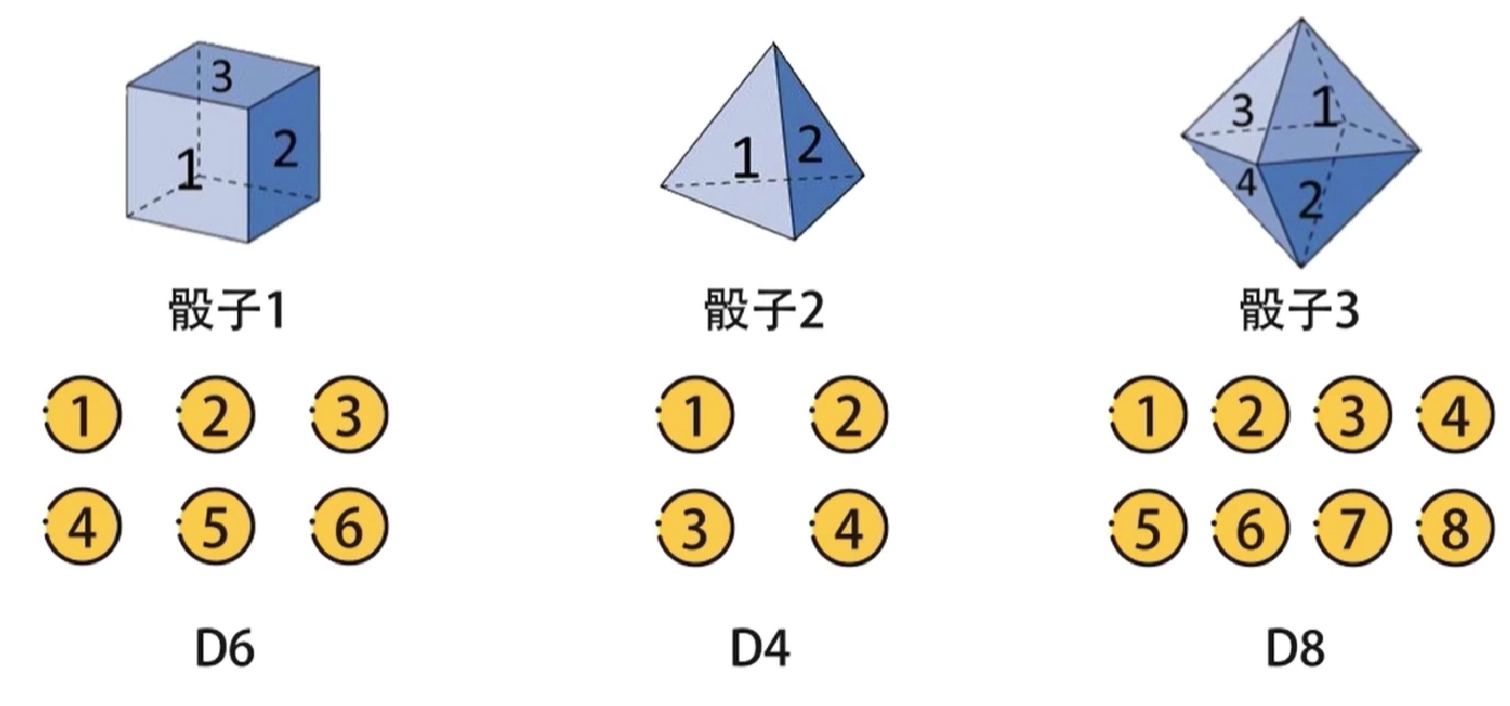
在不观察的情况下,从三个骰子中随机选一个,进行抛掷,结果可能是1-8中的任意数字。依照这种方式,随机选择骰子,重复抛掷,可以得到一串数字,这串数字对我们是可见的,并且直接记录下来了,因此将这串数字记作可见状态链

在抛掷的过程中,被我们随机选择的骰子编号也组成了一串序列,因为我们是随机选择的骰子,因此将这串序列称为隐含状态链
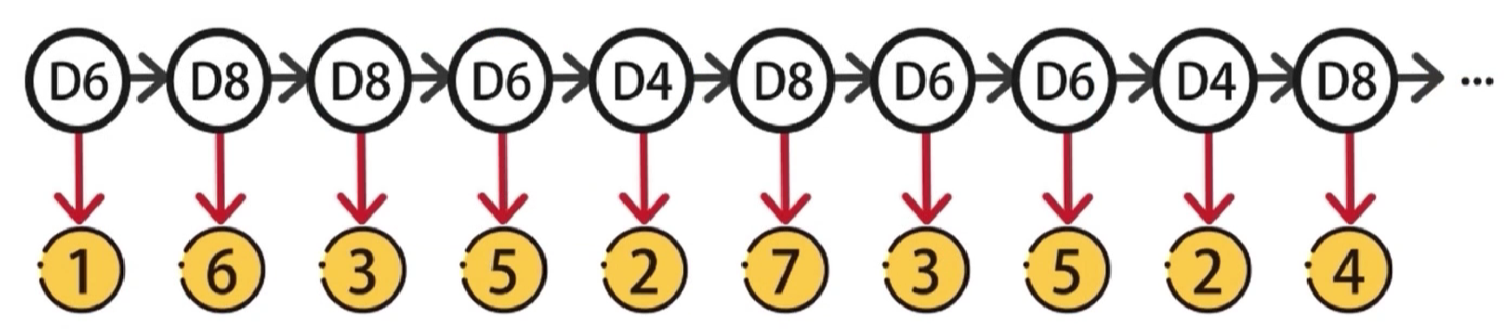
实验过程中产生了两个数据链,隐含状态链和可见状态链,隐马尔可夫模型=隐含状态链➕可见状态链
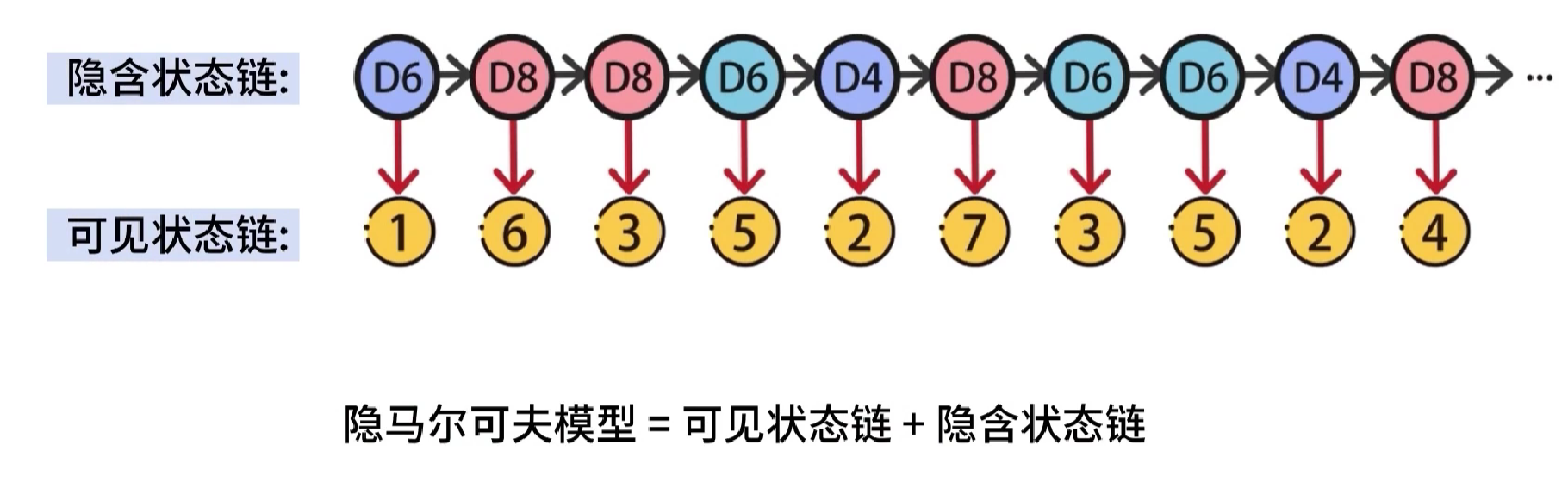
隐马尔可夫模型概念
隐马尔可夫模型(Hidden Markov Model),简称HMM,它是关于时序的概率模型,该模型包含随机生成的不可观测序列,该序列被称为状态序列,使用S表示,每个不可观测状态都会产生一个可观测的结果,这样会得到一个观测序列,使用O表示。
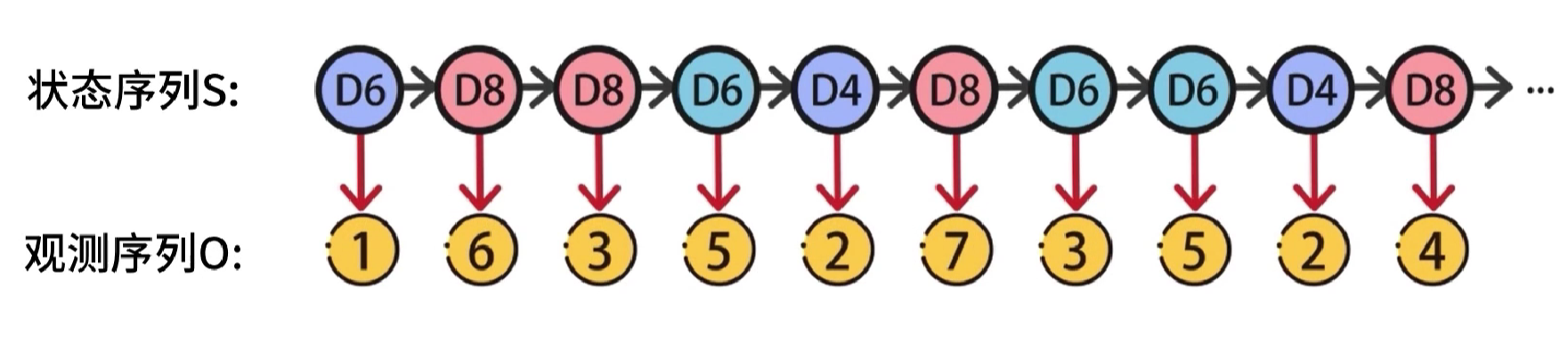
每个状态和时刻都会与一个时刻进行对应,如果有t个时刻,就产生了
s
1
→
s
t
,
o
1
→
o
t
s_1→s_t,o_1→o_t
s1→st,o1→ot,相当于一次一次掷骰子,t就代表第几次掷骰子
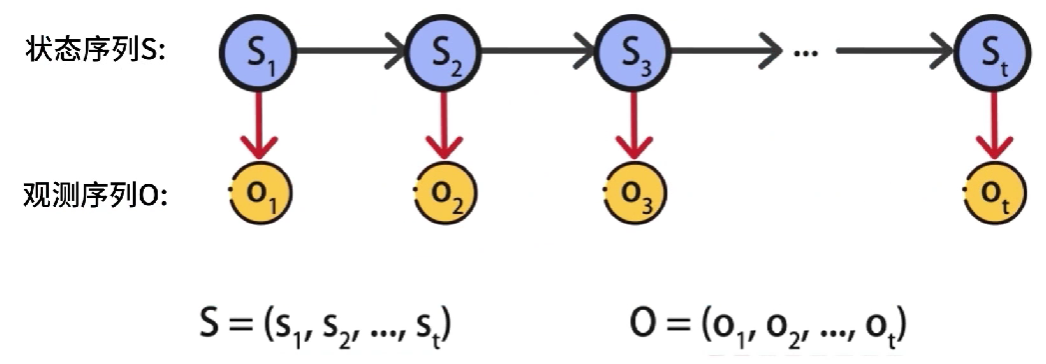
在HMM中,状态序列是隐藏的,无法被观测到,因此状态变量是一个隐变量,隐藏的状态序列是由一个马尔可夫链,随机生成的
隐马尔可夫模型的关键
在隐马尔可夫模型中, 包含了四个关键因素,分别是:
- 隐含状态
- 可见状态
- 隐含状态转换
- 可见状态输出
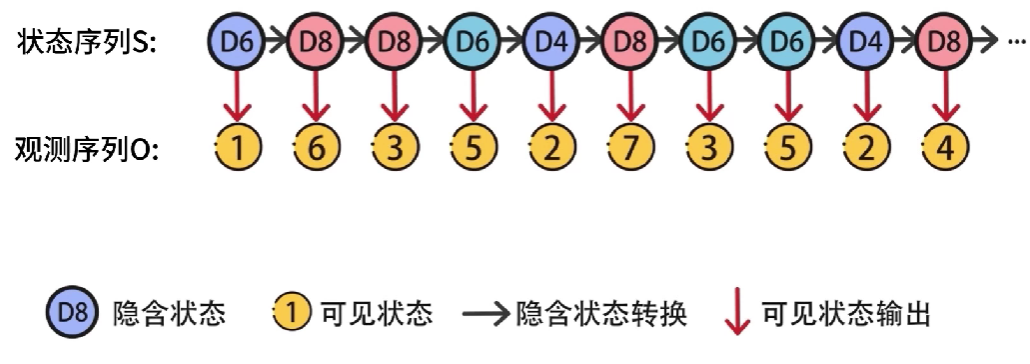
各个隐含状态之间会进行转换,存在着对应的转换概率
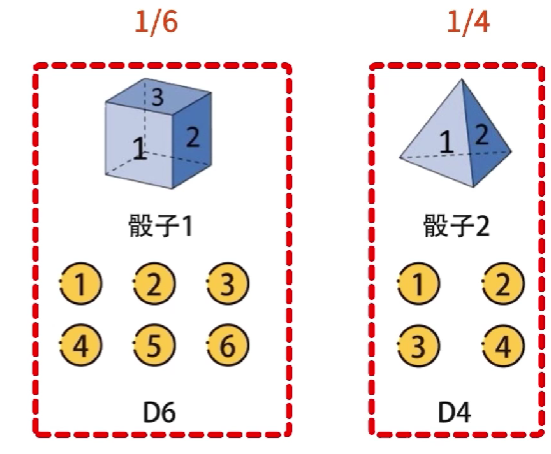
隐含状态会输出可见状态,隐含状态和可见状态之间有一个输出概率,不同隐含状态到可见状态的输出概率可能不同
例如,隐含状态D6输出可见状态1到6概率是 1 6 \cfrac{1}{6} 61,隐含状态D4输出可见状态1到4概率是 1 4 \cfrac{1}{4} 41,
隐马尔可夫模型的数学表示
为了进一步讨论隐马尔可夫模型,需要使用数学符号来表示HMM,其中包括隐含状态 Q Q Q和观测结果 V V V两个集合,状态转移概率矩阵 A A A,观测概率矩阵 B B B,初始状态概率向量 π \pi π,三个概率矩阵。
隐含状态与观测结果
例如,隐含状态集合
Q
=
{
q
1
,
q
2
,
.
.
.
,
q
n
}
Q = \{q_1,q_2,...,q_n\}
Q={q1,q2,...,qn}包括
q
1
到
q
n
n
q_1到q_n n
q1到qnn种状态
观测结果集合
V
=
{
v
1
,
v
2
,
.
.
.
,
v
m
}
V=\{v_1,v_2,...,v_m\}
V={v1,v2,...,vm}包括
v
1
到
v
m
m
v_1到v_m m
v1到vmm种可能的结果
在掷骰子的案例中,
n
=
3
q
1
,
q
2
,
q
3
对应
D
6
,
D
4
,
D
8
n=3\ \ \ q_1,q_2,q_3对应D_6,D_4,D_8
n=3 q1,q2,q3对应D6,D4,D8
m
=
8
v
1
到
v
8
对应数字
1
到
8
m=8 \ \ \ v_1到v_8对应数字1到8
m=8 v1到v8对应数字1到8

状态转移矩阵
状态转移的概率矩阵
A
A
A是一个是一个
N
∗
N
N*N
N∗N的矩阵
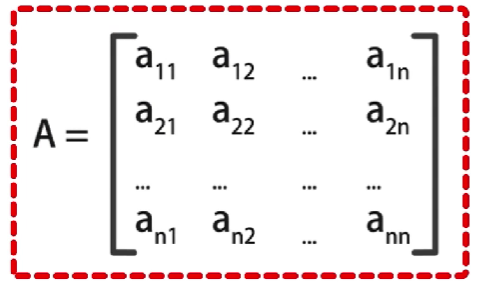
其中
a
i
j
a_{ij}
aij代表了状态
q
i
q_i
qi转移到状态
q
j
q_j
qj的概率
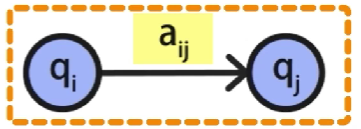
具体地,
a
i
j
等于在
s
t
=
q
i
的条件下,
s
t
+
1
=
q
j
的概率
a_{ij}等于在s_t = q_i的条件下,s_{t+1}=q_j的概率
aij等于在st=qi的条件下,st+1=qj的概率
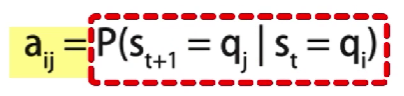
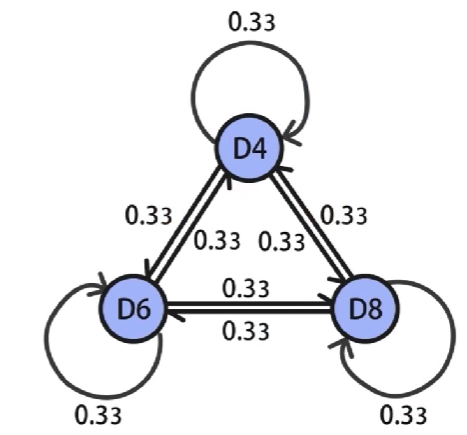
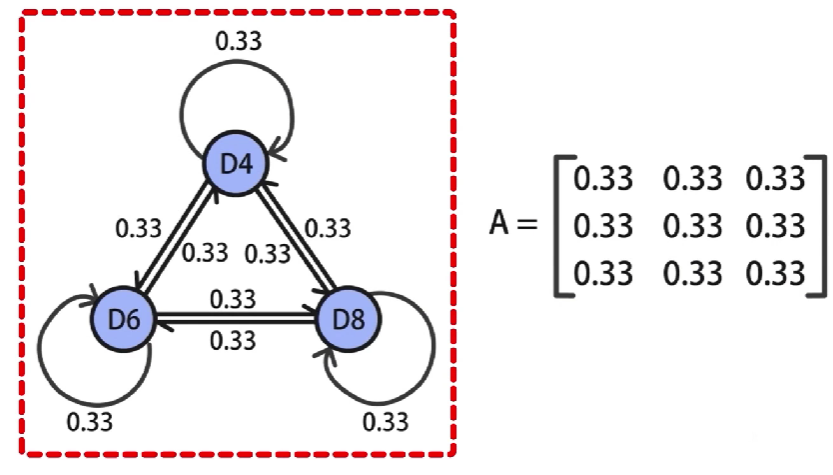
例如,3个骰子,选择任意骰子的概率都是
1
3
\cfrac{1}{3}
31,那么就得到了
3
∗
3
3*3
3∗3的状态转移概率矩阵,其中的每个元素都是
0.33
0.33
0.33,
观测概率矩阵
观测概率矩阵为 B B B,由于每一个状态 q q q都可以输出一个观测结果 v v v,因此B是一个 N ∗ M N*M N∗M的矩阵
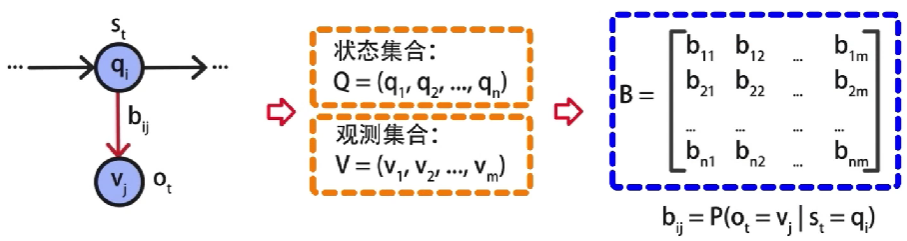
其中
b
i
j
b_ij
bij代表了在时刻
t
t
t,状态
q
i
q_i
qi输出观测结果
v
j
v_j
vj的概率。
例如,在掷骰子时,根据三种骰子的输出,可以得到一个 3 ∗ 8 3*8 3∗8的概率矩阵,第一行对应六面骰子,输出1到6的概率是1/6,输出7和8的概率是0,而第二行和第三行,分别代表投掷四面骰子和八面骰子的输出1到8的概率
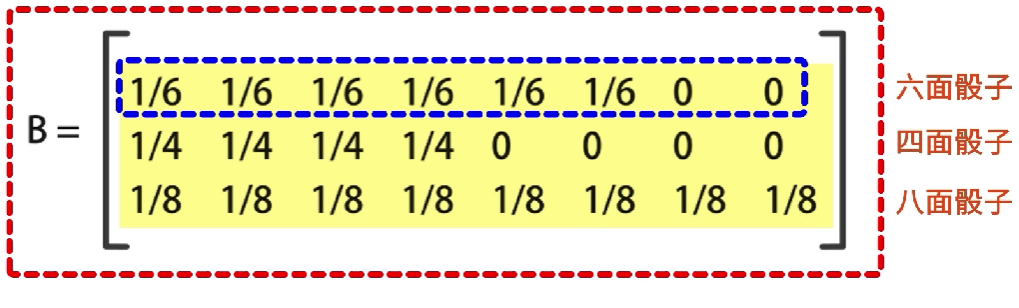
初始状态概率向量
初始状态的概率向量是
π
\pi
π,它是一个
N
∗
1
N*1
N∗1的列向量,
π
i
\pi_i
πi代表在时刻
t
=
1
t=1
t=1时,状态为
q
i
q_i
qi的概率,例如,掷骰子时,三种骰子的概率都是1/3

小结
π
和
A
\pi和A
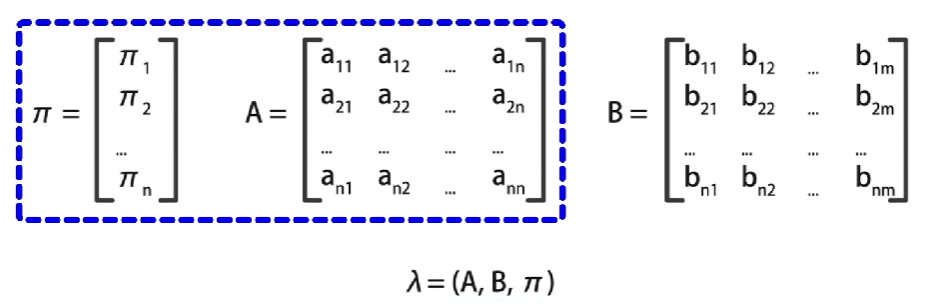
π和A确定了隐藏的马尔可夫链,也就是如何生成不可观测的状态序列
S
S
S,
B
B
B确定了如何从隐藏状态产生观测状态序列
O
O
O,隐马尔可夫模型由
A
、
B
、
π
A、B、\pi
A、B、π共同决定,使用三元符号
λ
=
(
A
,
B
,
π
)
λ=(A,B,\pi)
λ=(A,B,π)表示。
参考视频:什么是HMM隐马尔可夫模型,自然语言处理中的最基础算法之一_哔哩哔哩_bilibili