广度优先遍历详解

news2025/1/13 15:35:54

前言

广度优先搜索不同于深度优先搜索，它是一层层进行遍历的，因此需要先入先出的队列而非先入后出的栈进行遍历。由于是按层次进行遍历，广度优先搜索时按照“广”的方向进行遍历的

一、工作原理

我们构造这样一个图（如图1），并通过C++实现BFS，本文处理的图比二叉树要更复杂，如果时针对二叉树的BFS，程序会更为简单

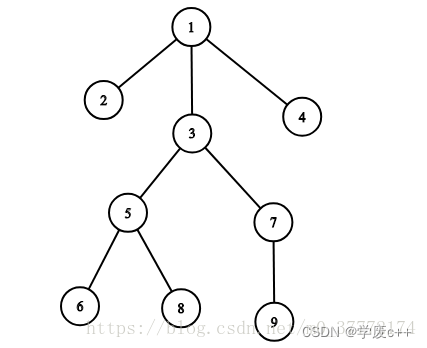
算法过程：

1.将根节点放入队列中

2.从队列中取出第一个元素，将队列中的第一个元素弹出

3.将所取得元素的全部节点加入队列中

4.判断队列是否为空

a. 若是，则结束

b.若不是，则跳到第二步

二、模板

由于是二维矩阵，需要q队列需要存储(x, y)，所以需要定义结构体node

struct node
{
	int x;
	int y;
};

为了减少推入队列的繁琐操作太多可以写一个函数循环利用

void p(int x, int y)
{
	node tmp;
	tmp.x = x;
	tmp.y = y;
	q.push(tmp);
}

函数模板

void bfs()
{
    //将起点推入队列
	
	while(!q.empty()) //保证队列不为空
	{
		node xy; //队列的定义是node类型，推进队列也要是node类型的！
		xy = q.front(); //拿走队头元素
		q.pop(); //细节出队
		
		if(判断是否为终点或其他出口)
		{
			退出等其他操作
		}
		
		for(int i = 1（0或1都行）; i <= （4个或8个方向）; i++)
		{
			int nx = xy.x + dx[i];//确定下一步的位置
			int ny = xy.y + dy[i];
            //出界与访问的判断
			if(nx >= 1 && nx <= n && ny >= 1 && ny <= m && !vis[nx][ny] && 其他判断条件)
			{
				vis[nx][ny] = true; //将新的点标记
				p(nx, ny) //nx, ny推进队列
			}
		}
	}
}

三、主要应用

(一)最短路径问题

题目描述

小明置身于一个迷宫，请你帮小明找出从起点到终点的最短路程。小明只能向上下左右四个方向移动。

输入格式

输入包含多组测试数据。输入的第一行是一个整数T，表示有T组测试数据。每组输入的第一行是两个整数N和M（1<=N,M<=100）。接下来N行，每行输入M个字符，每个字符表示迷宫中的一个小方格。字符的含义如下： ‘S’：起点 ‘E’：终点 ‘-’：空地，可以通过 ‘#’：障碍，无法通过输入数据保证有且仅有一个起点和终点。

输出格式

对于每组输入，输出从起点到终点的最短路程，如果不存在从起点到终点的路，则输出-1。

样例输入
1
5 5
S-###
-----
##---
E#---
样例输出
9
参考代码
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#define ll long long
using namespace std;

struct node
{
	int x;
	int y;
};

char a[105][105];
int vis[105][105], flag = false;
int dx[5] = {0, -1, 1, 0, 0};
int dy[5] = {0, 0, 0, -1, 1};
int n, m, sx, sy, cnt = 0, maxx = 0;
queue <node> q;

void p(int x, int y)
{
	node tmp;
	tmp.x = x;
	tmp.y = y;
	q.push(tmp);
}

void bfs()
{
	p(sx, sy);
	
	while(!q.empty())
	{
		node xy;
		xy = q.front();
		q.pop();
		
		if(a[xy.x][xy.y] == 'E')
		{
			cout<<vis[xy.x][xy.y]<<endl;
			flag = true;
			return;
		}
		
		for(int i = 1; i <= 4; i++)
		{
			int nx = xy.x + dx[i];
			int ny = xy.y + dy[i];

			if(nx >= 1 && nx <= n && ny >= 1 && ny <= m && vis[nx][ny] == 0 && (a[nx][ny] == 'E' || a[nx][ny] == '-'))
			{
				vis[nx][ny] = vis[xy.x][xy.y] + 1;
				p(nx, ny);
			}
		}
	}
}

int main()
{
	int t;
	cin>>t;
	
	for(int v = 1; v <= t; v++)
	{
		cin>>n>>m;
		
		memset(a, '#', sizeof(a));
		memset(vis, 0, sizeof(vis));
		
		for(int i = 1; i <= n; i++)
		{
			for(int j = 1; j <= m; j++)
			{
				cin>>a[i][j];
				if(a[i][j] == 'S')
				{
					sx = i;
					sy = j;
				}
			}
		}

		bfs();
		
		if(!flag)
			cout<<-1<<endl;
		flag = false;
	}
	
	return 0;
}