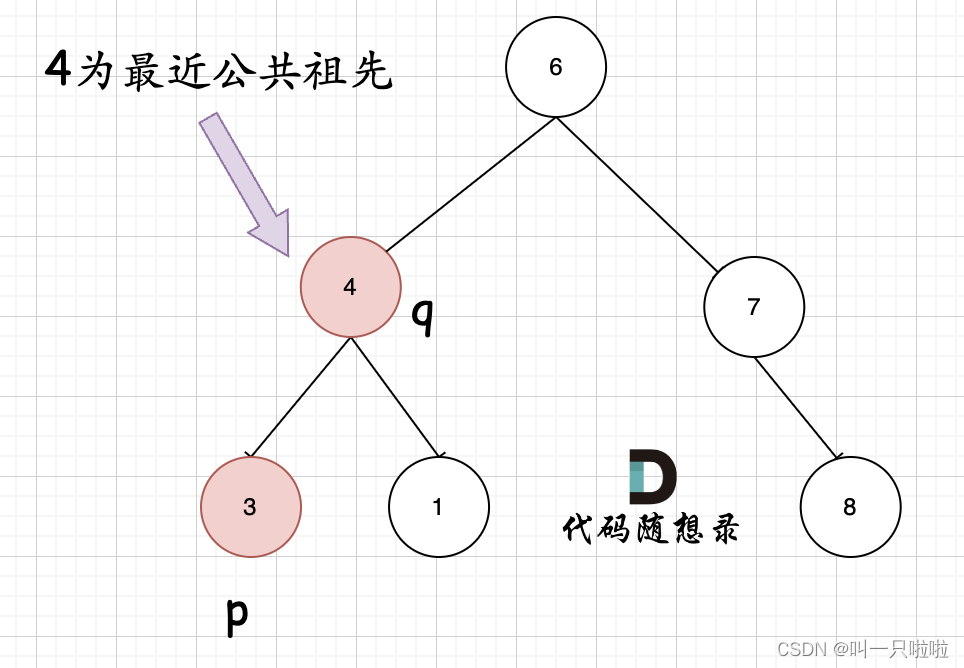
巴以冲突爆发后，许多配置不当的安全摄像头正暴露给黑客活动分子，使其周遭人员面临巨大安全风险。

Cyber​​news 研究人员发现，在以色列至少有165 个暴露的联网 RTSP 摄像头，在巴勒斯坦有 29 个暴露的 RTSP 摄像头。在巴勒斯坦，曝露的摄像头大部分位于约旦河西岸，这可能与以色列对加沙地带的电力封锁有关。

RTSP 代表实时流协议，虽然这种通信系统对于传输实时数据很有用，但它既不提供加密也不提供针对密码猜测的锁定机制。也就是说，这些摄像头对任何人都呈开放状态。

研究人员警告称，只要凭借一些众所周知的软件工具和基本教程，仅需要掌握基本技能就可以找到摄像头并暴力破解登录凭证。

获得访问权限后，这些摄像头最大的风险是能够查看实时画面，进而可用于监视、侦察或收集敏感信息。如果摄像头位于私人或敏感区域，则可能会侵犯人们的隐私，个人信息、日常生活或机密对话可能会被记录和滥用。这些信息可用于情报收集、间谍或勒索活动。

虽然个人面临风险，但攻击者主要感兴趣的是组织甚至政府设施。对其 RTSP 摄像头的访问可能为攻击者渗透摄像头所连接的网络提供了立足点。一旦进入网络，就可以横向移动以危害其他系统或窃取数据。

此外，研究人员还警告了另一种场景，即攻击者可能会操纵摄像头来显示误导性信息。比如改变摄像头方向来隐藏某些事件，或者让事情看起来好像发生了，但实际上并没有发生。

研究人员认为，分离和加密以及可靠的凭证是保护 RT​​SP 摄像头的有效策略，所有安全摄像头或其他 IP 摄像头都应连接到具有端到端加密或 WPA2（如果网络是无线）的单独受保护子网。