---

1、什么是贪心算法

贪心应当是一个策略，通过局部找到最优，来找到全局最优。它把解决问题的过程分为若干步，解决每一步的时候，都选择当前看起来最优的解法，通过这样做希望得到全局最优解。

看三个问题

找零问题。我有四种无限量的钞票，20，10，5，1，如何凑齐46？

现在把目光放到我有的每一个数字上，这时候就是划分成小问题了。

局部最优，通俗理解就是每一小步都要最接近目标的选择，不管后续如何。

所以这里会是这样选择，两个20，一个5，一个1。

---

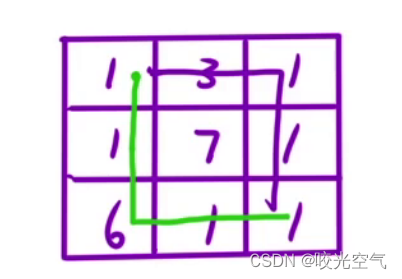
最小路径问题。这个在动规篇里提到过。假设一个二维数组，每个位置都有数，从左上角走到右下角，只能向右或向下，求最小的路径和，也就是每一步走到的位置的数字，所有的加起来应当最小。

既然要最小，那么每一步走之前，比较右边和下边两个数字哪个更小，就挑选哪个。我们希望最后生成的路径的和最小，只是在这个问题，贪心并不一定找到最小。下图中绿线就是贪心路径，紫线才是真实答案。

---

背包问题。有一些东西，每个东西都有自己的体积和价值，拿一些东西装满背包，背包最大容量为8。v是容量，w是价值，求最大价值。

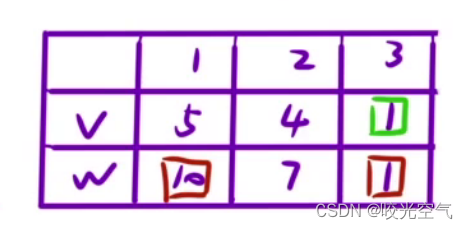
如果看体积，那么可以选择8个体积为1的，如果看价值，那么按照贪心算法，可以选择体积为5，价值为10的那个，选1个，然后再选3个体积为1，价值为1的那个。但是实际上答案应当是两个体积为4，价值为7的，这样最大价值就是14。

2、特点

贪心策略的提出是没有标准和模板。动规我们有常用的以某个位置为结尾，或者一类问题的比较通用的状态表示，以及还可以根据经验来提出状态。但贪心策略的提出千奇百怪，没法归纳出一个通用的表示，只能通过自己多做，多看，每次都分析一下题目再去写。

贪心策略有可能是错误的，证明它的错误很简单，举一个反例就行，就像上面的背包和路径问题；但是证明其正确是不简单的，这里就用到了数学方法。

3、学习方向

贪心的策略很多很多，怎么找到这个策略，有时也难以清楚地讲解出来。遇到不会的贪心题很正常，试着去解，按照以前解过的题目的解法去做就好。每次做题，都把这道题用到的策略记下来，以后也许会用到。

贪心的每篇博客最后都会写上证明。如果不想看证明，只想知道代码可以不用看这部分。

结束。