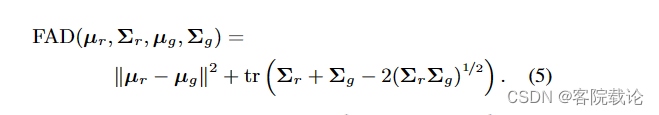使用真实数据

当你在研习机器学习时，最好是使用真实世界中的数据，而不是采用人工数据。巧的是，数以千计的数据集可供选择，涵盖了各种领域。

• 流行的开放数据存储库：
  • OpenML.org
  • Kaggle.com
  • paperswithcode.com
  • UC Irvine Machine Learning Repository
  • Amazon’s AWS datasets
  • TensorFlow datasets
• 元门户数据库：
  • DataPortals.org
  • OpenDataMonitor.eu
• 其他流行的开房数据集：
  • Wikipedia’s list of machine learning datasets
  • Quora.com
  • The datasets subreddit

本文数据来自于 StatLib 仓库的加州房价数据（见下图），它是基于 1990 年加利福尼亚州人口普查的数据，而不是最近的数据，不必过于纠结，我们的重心在于研习机器学习，并非是在讨论房价的问题。

看图说话

机器学习的首要任务，是利用加州人口普查数据，建立一个该州房价的模型。你的模型应该从这些数据中学习，并能够在给定所有其他指标的情况下，预测任何地区的房屋中位数价格。

框架问题

建立一个模型可能并不是最终目标，公司期望使用该模式如何从中获益？故而，了解目标是至关重要的，因为它将决定该如何去构建问题、将选择哪些算法、将使用哪些性能度量来评估您的模型，以及您将花费多少精力来调整它。

你的模型的输出(一个地区的房价中位数的预测)将被馈送到另一个机器学习系统(见下图)，以及许多其他的这个下游系统将决定它是否值得在一个给定的领域投资。做好这一点至关重要，因为它直接影响收入。

目前的解决方案是什么样的(如果有的话)。目前的情况往往会给你一个性能的参考，以及如何解决问题
的见解。该地区的房价目前是由专家手动估算的一个团队收集有关该地区的最新信息，当他们无法得到房价中位数时，他们使用复杂的规则来估算。

这既费钱又费时，而且他们的估计也不准确，在他们设法找出实际中位房价的情况下，他们常常意识到自己的估计误差超过30%。这就是为什么该公司认为，考虑到有关该地区的其他数据，建立一个预测该地区房价中值的模型将是有用的。人口普查数据看起来是一个很好的数据集，因为它包
括数千个地区的房屋价格中位数，以及其他数据。

管道

数据处理组件的序列称为数据管道。管道在机器学习系统中非常常见，因为有很多数据要操作，很多数据转换要应用。

组件通常异步运行。每个组件都拉入大量数据，对其进行处理，并将结果吐出到另一个数据存储中。然后，过了一段时间，管道中的下一个组件拉入该数据并输出它自己的输出。每个组件都是相当独立的:组件之间的接口仅仅是数据存储。这使得系统易于掌握(借助数据流
图)，不同的团队可以专注于不同的组件。此外，如果一个组件坏了下游组件通常可以继续正常运行(至少一段时间)，只需要使用坏掉的组件的最后一个输出。这使得体系结构相当健壮。

另一方面，如果没有实现适当的监视，一个损坏的组件可能在一段时间内不会被注意到。数据变得陈旧，整个系统的性能下降。

虽然有了这些信息，可以开始设计你的系统，但请回答，它是监督、无监督、半监督、自我监督、或强化学习任务？它是一个分类任务、回归任务，抑或是其它别的什么？你应该使用批量学习还是在线学习技术呢？

你能回答出来了吗？这显然是一个典型的监督学习任务，因为模型可以用带标签的示例进行训练(每个示例都带有预期输出，即该地区的房价中值)。这是一个典型的回归任务，因为模型将被要求预测一个值。更具体地说，这是一个多元回归问题，因为系统将使用多个特征进行预测(地区的人口、中位数收入等)。这也是一个单变量回归问题，因为我们只是试图预测每个地区的一个单一值。如果我们试图预测每个地区的多个值，这将是一个多元回归问题。最后，没有连续的数据流进入系统，没有特别的需要来适应快速变化的数据，数据足够小，可以放入内存中，所以普通的批处理学习应该做得很好。

选择性能度量

回归问题的一个典型性能度量是均方根误差(RMSE)。它给出了系统在其预测中通常会产生多大误差的概念，较大误差的权重较高。公式给出了计算RMSE的数学公式。

注意：

这个方程介绍了我将在本书中使用的几个非常常见的机器学习符号：

• m 是您测量RMSE 的数据集中的实例数。

  例如，如果您在 2,000 个地区的验证集上评估 RMSE，则 m = 2,000。

• x(i) 是数据集中第i 个实例的所有特征值（不包括标签）的向量，y(i) 是其标签（该实例的所需输出值）。 例如，如果数据集中的第一个区位于经度 –118.29°，纬度 33.91°，有 1,416 名居民，收入中位数为 38,372 美元，房屋价值中位数为 156,400 美元（暂时忽略其他特征）， 然后：

  

和：

• X是一个矩阵，包含数据集中所有实例的所有特征值（不包括标签）。 每个实例一行，第 i 行等于 x(i) 的转置，记为 (x(i))⊺.3 — 例如，如果第一区如上所述，则矩阵 X 如下所示：

  

• h 是系统的预测函数，也称为假设。 当给定系统一个实例的特征向量 x(i) 时，它会输出该实例的预测值 ŷ(i) = h(x(i))（ŷ 发音为“y-hat”）。 — 例如，如果您的系统预测第一区的房价中位数为 158,400 美元，则 ŷ(1) = h(x(1)) = 158,400。 该地区的预测误差为 ŷ(1) – y(1) = 2,000。

• MSE(X,h) 是使用假设 h 在一组示例上测量的成本函数。

我们使用小写斜体表示标量值（例如 m 或 y(i)）和函数名称（例如 h），使用小写粗体表示向量（例如 x(i)），使用大写粗体表示矩阵（例如 X）。

尽管RMSE通常是回归任务的首选性能度量，但在某些上下文中，您可能更喜欢使用其他函数。例如，如果有许多离群的地区。在这种情况下，你可以考虑使用平均绝对误差(MAE，也称为平均绝对偏差)，如下公式所示：

RMSE和MAE都是度量两个向量之间距离的方法:预测向量和目标值向量。各种距离测量或规范是可能的:

• 计算平方和的根 (RMSE) 对应于欧几里得范数：这是我们都熟悉的距离概念。 它也称为 ℓ2 范数，记作 ∥ · ∥2（或简称 ∥ · ∥）。
• 计算绝对值之和 (MAE) 对应于 ℓ1 范数，记为 ∥ · ∥1。 这有时被称为曼哈顿范数，因为如果您只能沿着正交的城市街区行驶，它会测量城市中两点之间的距离。
• 更一般地，包含 n 个元素的向量 v 的 ℓk 范数定义为 ∥v∥k = (|v1|k + |v2|k + … + |vn|k)1/k。 ℓ0 给出向量中非零元素的数量，ℓ∞ 给出向量中的最大绝对值。

范数指数越高，越注重大值而忽视小值。 这就是 RMSE 比 MAE 对异常值更敏感的原因。 但是，当异常值呈指数级稀有时（例如在钟形曲线中），RMSE 表现非常好并且通常是首选。

检查假设

最后，列出并验证到目前为止(您或其他人)所做的假设是一个很好的实践，这可以帮助您尽早发现严重的问题。例如，您的系统输出的地区价格将被输入到下游机器学习系统，并且您假设这些价格将被如此使用。但是，如果下游系统将价格转换成类别(例如，“便宜”、“中等”或“昂贵”)，然后使用这些类别而不是价格本身呢?在这种情况下，获得完全正确的价格一点也不重要;您的系统只需要获得正确的类别。如果是这样的话，那么这个问题应该被定义为一个分类任务，而不是一个回归任务。你不想在做了几个月的回归系统之后发现这个问题。

幸运的是，在与负责下游系统的团队交谈后，您确信他们确实需要实际价格，而不仅仅是类别。太好了!一切就绪，绿灯亮了，现在就可以开始编码了!

下载数据

在典型环境中，您的数据可在关系数据库或其他一些常见数据存储中使用，。

要访问它，您首先需要获取凭据和访问授权并熟悉数据架构。 然而，在这个项目中，事情要简单得多：您只需下载一个压缩文件 housing.tgz，其中包含一个名为 housing.csv 的逗号分隔值 (CSV) 文件以及所有数据。

通常最好编写一个函数来为您执行此操作，而不是手动下载和解压缩数据。 如果数据定期更改，这尤其有用：您可以编写一个小脚本，使用该函数来获取最新数据（或者您可以设置一个计划作业以定期自动执行此操作）。 如果您需要在多台计算机上安装数据集，自动化获取数据的过程也很有用。

from pathlib import Path
import pandas as pd
import tarfile
import urllib.request

def load_housing_data():
    tarball_path = Path("datasets/housing.tgz")
    if not tarball_path.is_file():
        Path("datasets").mkdir(parents=True, exist_ok=True)
        url = "https://github.com/ageron/data/raw/main/housing.tgz"
        urllib.request.urlretrieve(url, tarball_path)
        with tarfile.open(tarball_path) as housing_tarball:
            housing_tarball.extractall(path="datasets")
    return pd.read_csv(Path("datasets/housing/housing.csv"))

housing = load_housing_data()

当调用 load_housing_data() 时，它会查找 datasets/housing.tgz 文件。 如果没有找到，它会在当前目录中创建 datasets 目录，从 Ageron/data GitHub 存储库下载 housing.tgz 文件，并将其内容提取到 datasets 目录中 ; 这将创建 datasets/housing 目录，其中包含 housing.csv 文件。 最后，该函数将此 CSV 文件加载到包含所有数据的 Pandas DataFrame 对象中，并返回它。

创建测试集

在这个阶段自愿搁置部分数据可能看起来很奇怪。 毕竟，您只是快速浏览了一下数据，在决定使用哪些算法之前，您当然应该了解更多相关信息，对吗？ 这是事实，但你的大脑是一个令人惊奇的模式检测系统，这也意味着它很容易过度拟合：如果你查看测试集，你可能会在测试数据中偶然发现一些看似有趣的模式，从而引导你选择 一种特殊的机器学习模型。 当您使用测试集估计泛化误差时，您的估计将过于乐观，并且您将启动一个性能不如预期的系统。 这称为数据窥探偏差。

import numpy as np

def shuffle_and_split_data(data, test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    test_indices = shuffled_indices[:test_set_size]
    train_indices = shuffled_indices[test_set_size:]
    return data.iloc[train_indices], data.iloc[test_indices]

好了，这个工作，但它并不完美:如果你再次运行这个程序，它将生成一个不同的测试集!随着时间的推移，你(或你的机器学习算法)将看到整个数据集，这是你要避免的

一种解决方案是在第一次运行时保存测试集，然后在后续运行中加载。另一个选项是在调用np.random.permutation()之前设置随机数生成器的seed(例如，使用np.random.seed(42))。，以便它总是生成相同的打乱索引。

但是，这两种解决方案在下次获取更新的数据集时都会中断。即使在更新数据集之后也要进行稳定的训练/测试分割，常见的解决方案是使用每个实例的标识符来决定是否应该在测试集中运行(假设实例具有唯一和不可变的标识符)。例如，如果哈希值低于或等于最大哈希值的20%，则可以计算每个实例的标识符的散列，并将该实例放入测试集中。这可以确保测试集在多个运行期间保持一致，即使刷新数据集也是如此。新的测试集将包含20%的新实例，但它不会包含以前在训练集中的任何实例。

from zlib import crc32

def is_id_in_test_set(identifier, test_ratio):
    return crc32(np.int64(identifier)) < test_ratio * 2**32

def split_data_with_id_hash(data, test_ratio, id_column):
    ids = data[id_column]
    in_test_set = ids.apply(lambda id_: is_id_in_test_set(id_, test_ratio))
    return data.loc[~in_test_set], data.loc[in_test_set]

不幸的是，住房数据集没有标识符列。最简单的解决方案是使用行索引作为ID:

housing_with_id = housing.reset_index()  # adds an `index` column
train_set, test_set = split_data_with_id_hash(housing_with_id, 0.2, "index")

如果使用行索引作为唯一标识符，则需要确保将新数据追加到数据集的末尾，并且不会删除任何行。果这是不可能的，那么你可以尝试使用最稳定的功能来建立一个唯一的标识符。例如，一个地区的纬度和经度保证在几百万年内是稳定的，因此您可以将它们组合成一个ID，如下所示:

housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_data_with_id_hash(housing_with_id, 0.2, "id")

Scikit-Learn提供了一些函数，以各种方式将数据集拆分为多个子集。最简单的函数train_test_split()，它的功能与我们前面定义的shuffle_and_split_data ()函数非常相似，只是增加了几个特性。首先，有一个random_state参数，它允许您设置随机生成器种子。其次，您可以向它传递具有相同行数的多个数据集，它将按照相同的索引将它们拆分(这是非常有用的，例如，如果你有一个单独的DataFrame标签):

from sklearn.model_selection import train_test_split

train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)

到目前为止，我们已经考虑了纯随机抽样方法。 如果您的数据集足够大（尤其是相对于属性数量而言），这通常没问题，但如果不是，您就会面临引入显着抽样偏差的风险。 当一家调查公司的员工决定给 1,000 个人打电话询问一些问题时，他们不会只是在电话簿中随机挑选 1,000 个人。 他们试图确保这 1000 人能够代表全体民众，了解他们想问的问题。 例如，美国人口中女性占 51.1%，男性占 48.9%，因此在美国进行的一项精心调查将尽力维持样本中的这一比例：511 名女性和 489 名男性（至少如果答案可能是这样的话） 因性别而异）。 这称为分层抽样：将总体分为称为层的同质子组，并从每个层中抽取正确数量的实例，以保证测试集能够代表总体。 如果进行调查的人使用纯粹随机抽样，则有大约 10.7% 的机会对女性参与者少于 48.5% 或超过 53.5% 的倾斜测试集进行抽样。 不管怎样，调查结果可能会有很大偏差。

假设你和一些专家聊天，他们告诉你，收入中位数是预测房价中位数的一个非常重要的属性。你可能想确保测试集代表了整个数据集中的各种收入类别。由于中位数收入是一个连续的数字属性，您首先需要创建一个收入类别属性。让我们更仔细地看看收入中位数的柱状图(回到图2-8):大多数收入中位数都聚集在1.5至6(即15,000至60,000美元)，但一些中等收入远远超过6。在数据集中为每个层提供足够数量的实例是很重要的，否则对层的重要性的估计可能会有偏差。这意味着你不应该有太多的阶层，每个阶层都应该足够大。下面的代码使用pd.cut()函数创建一个包含五个类别(标记为1到5)的income category属性;category 1的范围是0到1.5(即低于$15,000),category 2的范围是1.5到3，依此类推:

housing["income_cat"] = pd.cut(housing["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])

housing["income_cat"].value_counts().sort_index().plot.bar(rot=0, grid=True)
plt.xlabel("Income category")
plt.ylabel("Number of districts")
save_fig("housing_income_cat_bar_plot")  # extra code
plt.show()

现在您已准备好根据收入类别进行分层抽样。 Scikit-Learn 在 sklearn.model_selection 包中提供了许多拆分器类，这些类实现了各种策略来将数据集拆分为训练集和测试集。 每个拆分器都有一个 split() 方法，该方法返回同一数据的不同训练/测试拆分的迭代器。

准确地说，split()方法生成的是训练和测试指标，而不是数据本身。如果你想更好地估计你的模型的性能，有多个拆分是很有用的，当我们在本章后面讨论交叉验证的时候你会看到。例如，下面的代码生成同一数据集的10个不同的分层拆分:

from sklearn.model_selection import StratifiedShuffleSplit

splitter = StratifiedShuffleSplit(n_splits=10, test_size=0.2, random_state=42)
strat_splits = []
for train_index, test_index in splitter.split(housing, housing["income_cat"]):
    strat_train_set_n = housing.iloc[train_index]
    strat_test_set_n = housing.iloc[test_index]
    strat_splits.append([strat_train_set_n, strat_test_set_n])

现在就可以拆分了

strat_train_set, strat_test_set = strat_splits[0]

或者，因为分层抽样很常见，所以有一个更简单的方法，使用带stratify参数的train_test_split ()函数来获得单个拆分:

strat_train_set, strat_test_set = train_test_split(
    housing, test_size=0.2, stratify=housing["income_cat"], random_state=42)

让我们看看这是否像预期的那样工作。你可以从测试集中的收入类别比例开始:

使用类似的代码，您可以测量整个数据集中的收入类别比例。下图比较了总体数据集、分层抽样生成的测试集和纯粹随机抽样生成的测试集中的收入类别比例。如您所见，使用分层抽样生成的测试集的收入类别比例几乎与完整数据集中的收入类别比例相同，而使用纯粹随机抽样生成的测试集是倾斜的。

您不会再次使用income_cat列，所以您不妨删除它，将数据恢复到原始状态:

for set_ in (strat_train_set, strat_test_set):
    set_.drop("income_cat", axis=1, inplace=True)

我们在测试集生成上花了相当多的时间，这是有充分理由的:这是一个机器学习项目中经常被忽视但非常关键的部分。此外，当我们讨论交叉验证时，这些想法中的许多将是有用的。现在是时候进入下一个阶段了:探索数据。