动态规划的解题步骤可以分为以下五步,大家先好好记住
1.创建dp数组以及明确dp数组下标的含义 2.制定递推公式 3.初始化 4.遍历顺序 5.验证结果
根据打家劫舍的题意:两个直接相连的房子在同一天晚上被打劫会触发警报
所以我们制定出核心策略——偷东西只能隔一家偷!
接下来只要记住核心思想,围绕这个思想来解题就可以了!
核心思想 :如果偷了这家那么上一家就不能偷,如果不偷这一家那么上一家就可以偷
首先看第一题
198. 打家劫舍
这是一道标准的打家劫舍问题
运用动态规划解题步骤结合核心代码来进行解题
public int rob(int[] nums) {
int n = nums.length;
//dp数组下标的含义是抢劫到该房屋的最高金额
int[] dp = new int[n];
//递推公式:dp[i] = Math.max(nums[i-1] + dp[i-2],dp[i-1]);
//初始化
dp[0] = nums[0];
//遍历顺序 从后向前遍历
for(int i = 1;i < n;i++){
if(i >= 2){
dp[i] = Math.max(nums[i] + dp[i-2],dp[i-1]);
}else{
dp[i] = Math.max(nums[i],dp[i-1]);
}
}
//验证
return dp[n-1];
}213. 打家劫舍 II
这道题实际上是第一题的变招(看起来把屋子围起来了让小偷偷到钱财的难度增加了,但实际上小偷只需要转变一下思路也可以偷到很多钱 ^ ^ )
由于屋子围了起来,所以第一间屋子和最后一屋子现在是相邻的了
如果还是像刚才一样从头偷到尾那肯定是行不通的了。但是如果我避开这个“第一间屋子和最后一屋子现在是相邻的了”这个条件是不是还是从头偷到尾呢?
答案是可以的,以题目的示例二举例
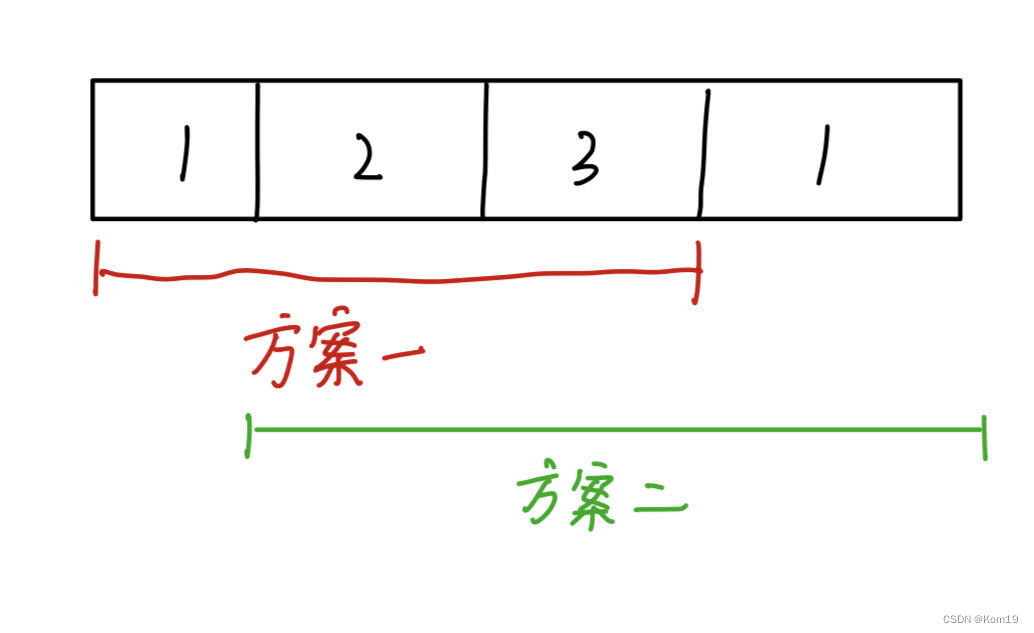
现在我们只需要指定两套方案,一套是从第一间偷到倒数第二间房子,另一套是从第二间偷到最后一间房子,然后比较两套方案哪个偷到的金额更大即可
接下来结合这个思想以及核心代码来编写代码
public int rob(int[] nums) {
if(nums.length == 0 || nums == null){
return 0;
}
if(nums.length == 1){
return nums[0];
}
if(nums.length == 2){
return Math.max(nums[0],nums[1]);
}
return Math.max(robMaxNumber(0,nums.length - 2,nums),robMaxNumber(1,nums.length - 1,nums));
}
public int robMaxNumber(int start,int end,int[] nums){
if(start == end){
return nums[start];
}
int[] dp = new int[nums.length];
dp[start] = nums[start];
dp[start + 1] = Math.max(nums[start] , nums[start+1]);
for(int i = start + 2;i <= end;i++){
dp[i] = Math.max(dp[i-2] + nums[i],dp[i - 1]);
}
return dp[end];
}337. 打家劫舍 III
这道题还是有点难度的,既用到了动态规划又用到了二叉树的知识,但是结合上核心思想还是很简单的
根据题意两个直接相连的房子在同一天晚上被打劫结合核心思想
如果偷了孩子节点那么父节点就不能偷了,如果偷了父节点那么子节点就不能偷了
我们可以用一个二维数组来表达偷了该节点所获得的最大金额以及不偷该节点所获得最大金额
//0表示不偷该节点 1表示偷该节点
int[][] res = new int[2][1];到这里动态规划需要解决的问题就解决了
ok解决完动态规划的部分接下来来看二叉树的部分需要解决的问题 —— 遍历顺序
由于我们先要知道孩子节点的情况才能做出下一步判断
所以我们使用后序遍历的方式对树进行遍历
解决完两个难点接下来结合核心思想来编写代码
public int rob(TreeNode root) {
int[][] result = robHelper(root);
return Math.max(result[0][0],result[1][0]);
}
public int[][] robHelper(TreeNode root) {
//表示偷还是不偷
int[][] res = new int[2][1];
//遇到空节点返回
if(root == null){
return res;
}
//从底部向上遍历所以是后序遍历
int[][] left = robHelper(root.left);
int[][] right = robHelper(root.right);
//不偷父节点所以要获取孩子节点的最大值
res[0][0] = Math.max(left[0][0],left[1][0]) + Math.max(right[0][0],right[1][0]);
//偷父节点所以不能偷孩子节点了
res[1][0] = left[0][0] + right[0][0] + root.val;
return res;
}总的来说只要结合了核心思想“偷这个就不能偷那个” 打家劫舍问题还是很简单的