SImilarity 搜索是一个问题，给定一个查询的目标是在所有数据库文档中找到与其最相似的文档。

一、介绍

        在数据科学中，相似性搜索经常出现在NLP领域，搜索引擎或推荐系统中，其中需要检索最相关的文档或项目以进行查询。在大量数据中，有各种不同的方法可以提高搜索性能。

        在本系列文章的第一部分中，我们研究了用于执行相似性搜索的 kNN 和倒排文件索引结构。正如我们所了解的，kNN是最直接的方法，而倒置文件索引则在其之上起作用，这表明在速度加速和精度之间进行权衡。然而，这两种方法都不使用可能导致内存问题的数据压缩技术，尤其是在数据集较大且RAM有限的情况下。在本文中，我们将尝试通过查看另一种称为产品量化的方法来解决此问题。

二、相似性定量化

        乘积量化是将每个数据集向量转换为短内存高效表示（称为 PQ 代码）的过程。不是完全保留所有向量，而是存储它们的简短表示。同时，产品量化是一种有损压缩方法，导致预测精度较低，但在实践中，该算法非常有效。

In general, quantization is the process of mapping infinite values to discrete ones.

2.1 训练

        首先，该算法将每个向量分成几个相等的部分——子向量。所有数据集向量的每个相应部分形成独立的子空间，并单独处理。然后对向量的每个子空间执行聚类算法。通过这样做，在每个子空间中创建多个质心。每个子向量都使用其所属质心的 ID 进行编码。此外，所有质心的坐标都会被存储起来供以后使用。

子空间质心也称为量子化向量。

在产品量化中，集群 ID 通常称为复制值。

        注意。在下图中，矩形表示包含多个值的向量，而正方形表示单个数字。

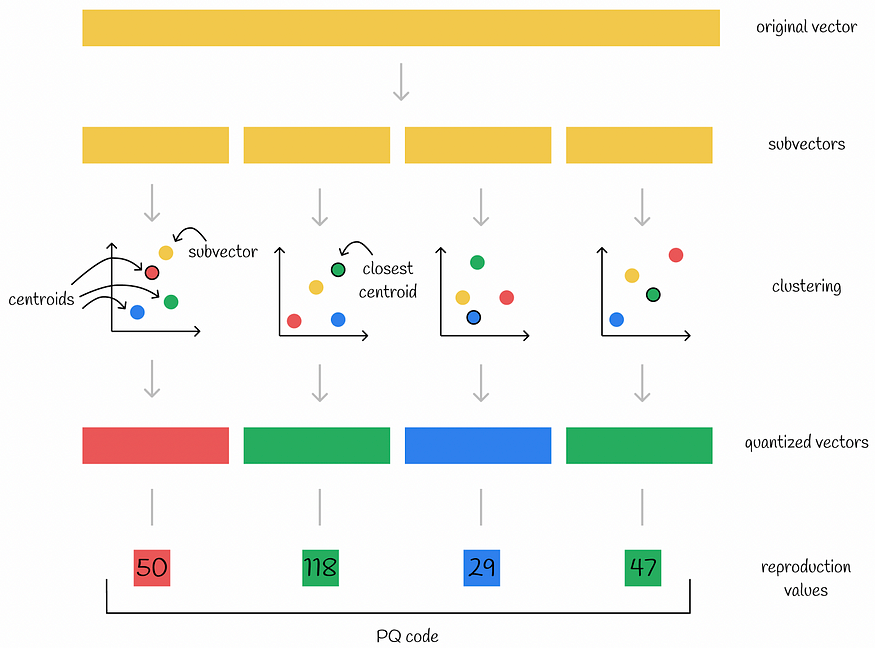
        使用量化进行编码

        因此，如果将原始向量分成 n 个部分，则可以对其进行编码 n 个数字 — 每个子向量的各个质心的 ID。通常，创建的质心数 k 通常被选为 2 的幂，以便更有效地使用内存。这样，存储编码向量所需的内存为 n * log（k） 位。

子空间内所有质心的集合称为密码本。对所有子空间运行 n 个聚类算法会生成 n 个单独的码本。

3.2 压缩示例

        想象一下，一个存储浮点数（1024 位）的大小为 32 的原始向量被分成 n = 8 个子向量，其中每个子向量由 k = 256 个簇中的一个编码。因此，对单个集群的 ID 进行编码需要 log（256） = 8 位。让我们比较两种情况下向量表示的内存大小：

• 原始向量：1024 * 32 位 = 4096 字节。
• 编码向量：8 * 8 位 = 8 字节。

最终压缩是512倍！这才是产品量化的真正力量。

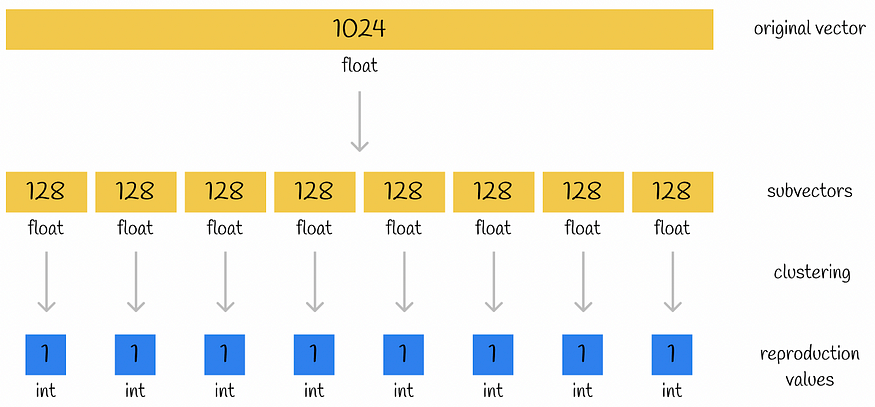
      量化示例。向量中的数字显示它存储了多少个数字。

        以下是一些重要注意事项：

• 该算法可以在向量的一个子集上进行训练（例如，创建集群）并用于另一个子集：一旦算法被训练，就会传递另一个向量数据集，其中使用每个子空间的已构建质心对新向量进行编码。
• 通常，选择 k 均值作为聚类分析算法。它的优点之一是聚类数 k 是一个超参数，可以根据内存使用要求手动定义。

三、推理

        为了更好地理解，让我们首先看一下几种幼稚的方法并找出它们的缺点。这也将帮助我们意识到为什么不应该正常使用它们。

3.1 简单的方法

        第一种朴素方法包括通过连接每个向量的相应质心来解压缩所有向量。之后，可以从查询向量计算到所有数据集向量的 L2 距离（或其他指标）。显然，这种方法有效，但它非常耗时，因为执行暴力搜索并在高维解压缩向量上执行距离计算。

        另一种可能的方法是将查询向量拆分为子向量，并根据其 PQ 代码计算从每个查询子向量到数据库向量相应量化向量的距离总和。因此，再次使用暴力搜索技术，这里的距离计算仍然需要原始向量维数的线性时间，就像前面的情况一样。

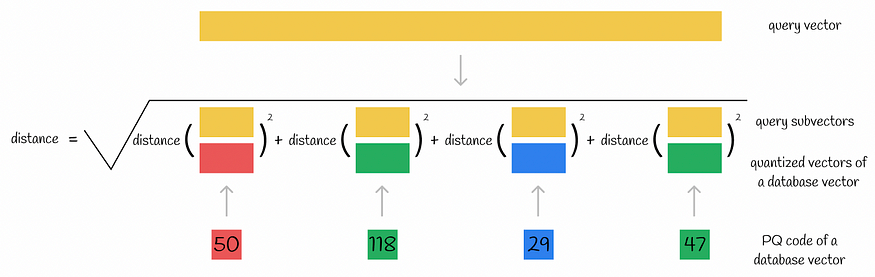
        使用朴素方法计算近似距离。该示例显示了欧氏距离作为度量。

        另一种可能的方法是将查询向量编码为 PQ 代码。然后直接使用此PQ代码来计算到所有其他PQ代码的距离。然后，具有距离最短的相应 PQ 代码的数据集向量被视为与查询最近的邻居。这种方法比前两种方法更快，因为始终在低维 PQ 代码之间计算距离。但是，PQ 代码由集群 ID 组成，这些集群 ID 没有太多语义含义，可以被视为显式用作实变量的分类变量。显然，这是一种不好的做法，这种方法可能会导致预测质量不佳。

3.2 优化的方法

        查询向量分为子向量。对于其每个子向量，计算到相应子空间的所有质心的距离。最终，此信息存储在表 d 中。

获取存储部分查询子向量到质心距离的表 d

计算出的子矢量到质心距离通常称为部分距离。

通过使用此子向量到质心的距离表 d，可以通过其 PQ 代码轻松获得从查询到任何数据库向量的近似距离：

1. 对于数据库向量的每个子向量，找到最接近的质心 j（通过使用 PQ 代码中的映射值），并获取从该质心到查询子向量 i 的部分距离 d[i][j]（通过使用计算的矩阵 d）。
2. 所有部分距离均求平方和相加。通过取该值的平方根，得到近似的欧几里得距离。如果您还想知道如何获取其他指标的近似结果，请导航到下面的“其他距离指标的近似值”部分。

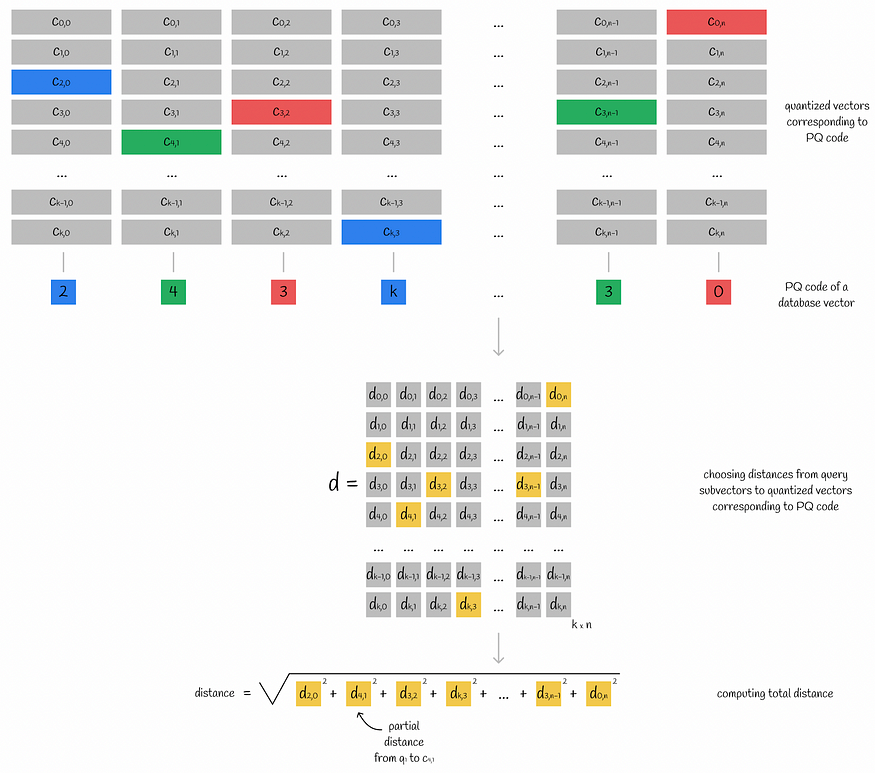
使用 PQ 代码和距离表计算从查询到数据库向量的距离

使用此方法计算近似距离假定部分距离 d 非常接近查询子向量和数据库子向量之间的实际距离 a。

然而，这个条件可能不满足，特别是当数据库子向量与其质心之间的距离c很大时。在这种情况下，计算会导致较低的准确性。

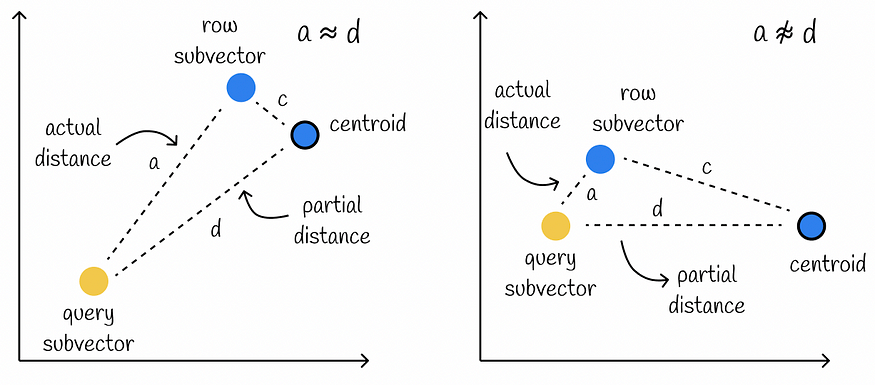
左边的例子显示了当实际距离非常接近部分距离（c很小）时的良好近似情况。在右侧，我们可以观察到一个糟糕的情况，因为部分距离比实际距离长得多（c 很大）。

获得所有数据库行的近似距离后，我们搜索具有最小值的向量。这些向量将是查询最近的邻居。

3.3 其他距离指标的近似值

        到目前为止，已经研究了如何使用部分距离来近似欧几里得距离。让我们也概括一下其他指标的规则。

        想象一下，我们想计算一对向量之间的距离度量。如果我们知道指标的公式，我们可以直接应用它来获得结果。但有时我们可以通过以下方式按部分完成：

• 两个向量都分为 n 个子向量。
• 对于每对相应的子向量，将计算距离度量。
• 然后将计算出的 n 个指标组合在一起，以产生原始向量之间的实际距离。

        该图显示了计算指标的两种方法。在左侧，度量公式直接应用于两个向量。在右侧，计算每对相应子向量的部分距离。然后使用聚合函数 h、g 和 f 将它们组合在一起。

        欧几里得距离是可以按零件计算的度量的一个例子。根据上图，我们可以选择聚合函数为 h（z） = z² ， g（z₀， z₁， ...， zn） = sum（z₀， z₁， ...， zn） 和 f（z） = √z。

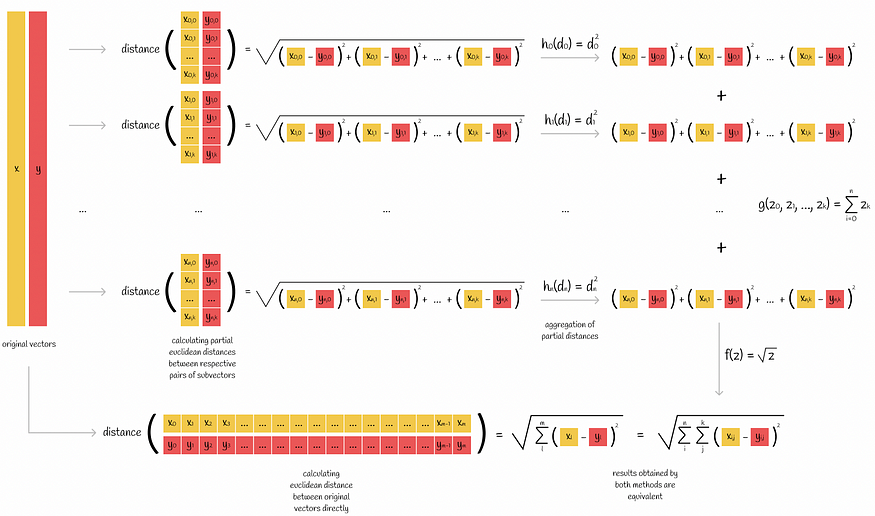
        欧氏距离可以按零件计算

        内积是这种度量的另一个例子，其聚合函数 h（z） = z， g（z₀， z₁， ...， zn） = sum（z₀， z₁， ...， zn） 和 f（z） = z。

        在产品量化的上下文中，这是一个非常重要的属性，因为在推理过程中，算法按零件计算距离。这意味着使用没有此属性的产品量化指标会更加成问题。余弦距离就是这种度量的一个例子。

        如果仍然需要使用没有此属性的指标，则需要应用其他启发式方法来聚合具有一定误差的部分距离。

3.4 性能

产品量化的主要优点是大量压缩存储为短PQ码的数据库向量。对于某些应用，这种压缩率甚至可能高于95%！但是，除了PQ码之外，还需要存储大小为k x n的矩阵d，其中包含每个子空间的量化向量。

产品量化是一种有损压缩方法，因此压缩率越高，预测精度降低的可能性就越大。

构建高效表示系统需要训练多个聚类算法。除此之外，在推理过程中，需要以蛮力方式计算k * n部分距离，并为每个数据库向量求和，这可能需要一些时间。

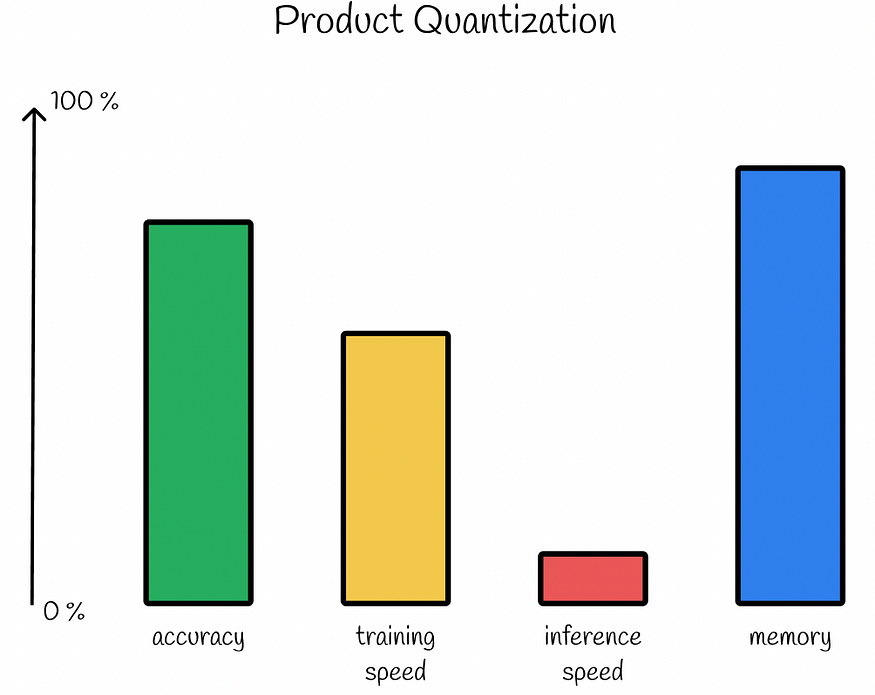
产品量化性能

四、Faiss库实现

Faiss（Facebook AI Search Similarity）是一个用C++编写的Python库，用于优化的相似性搜索。该库提供了不同类型的索引，这些索引是用于有效存储数据和执行查询的数据结构。

根据 Faiss 文档中的信息，我们将了解如何利用产品量化。

产品量化在 IndexPQ 类中实现。对于初始化，我们需要提供 3 个参数：

• d：数据中的维度数。
• M：每个向量的分裂数（与上面使用的 n 参数相同）。
• nbits：对单个集群 ID 进行编码所需的位数。这意味着单个子空间中的总聚类数将等于 k = 2^nbits。

对于相等的子空间维度分割，参数 dim 必须能被 M 整除。

存储单个向量所需的总字节数等于：

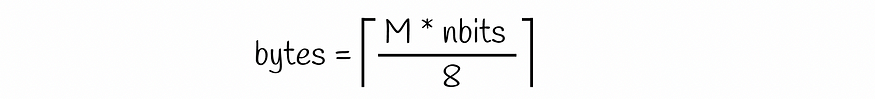
正如我们在上面的公式中看到的，为了更有效地使用内存，M * nbits 的值应该能被 8 整除。

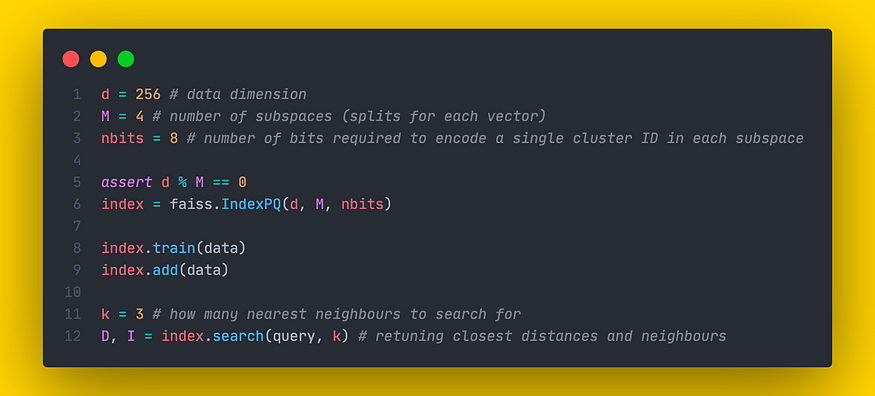
费斯对IndexPQ的实现

五、结论

        我们已经研究了信息检索系统中一种非常流行的算法，该算法可以有效地压缩大量数据。它的主要缺点是推理速度慢。尽管如此，该算法仍广泛用于现代大数据应用，特别是与其他相似性搜索技术结合使用。

        在本系列文章的第一部分中，我们介绍了倒排文件索引的工作流。事实上，我们可以将这两种算法合并为一种更有效的算法，它将拥有这两种算法的优势！这正是我们将在本系列的下一部分要做的事情。