文章目录
- 八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
- 1、(直接)插入排序
- 1.1、算法思想
- 1.2、排序过程图解
- 1.3、排序代码
- 2、希尔排序
- 3、冒泡排序
- 3.1、算法思想
- 3.2、排序过程图解
- 3.3、排序代码
- 4、(简单)选择排序
- 4.1、算法思想
- 4.2、排序过程图解
- 4.3、排序代码
- 5、堆排序
- 6、快速排序
- 7、归并排序
- 8、计数排序
- 8.1、算法思想
- 8.2、排序过程图解
- 8.3、排序代码

八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
下列算法默认都是对数组进行升序
1、(直接)插入排序
1.1、算法思想
-
插入排序是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序的具体步骤如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。


1.2、排序过程图解
-
从第一个元素开始,该元素可以认为已经被排序,取出下一个元素并记录到临时变量
tmp中,在已经排序的元素序列中从后向前扫描(end--),如果该元素(已排序)大于新元素,将该元素移到下一位置,如果该元素小于等于新元素,则直接在这个元素的后面把新元素放进来。

- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
1.3、排序代码
-
end指向当前要插入元素的前一个位置(end+1指向当前要插入元素的位置),tmp保存当前要插入的元素,在已经排序的元素序列中从后向前扫描,找到比新元素小的元素的时候(因为有序,这个位置前面的元素比这个元素更小),直接把新元素插入到这个位置的后面。//插入排序 void InsertSort(int *arr, int n) { for (int i = 0; i < n - 1; ++i) { //一趟 int end = i; int tmp = arr[end + 1]; while (end >= 0) { if (tmp < arr[end]) { arr[end + 1] = arr[end]; } else { break; } --end; } arr[end + 1] = tmp; } } -
时间复杂度计算:
-
最坏时间复杂度:数组元素原本是降序,现要求使其升序。那么每个元素需要移动或者比较的次数为:
- 第一个元素:
0次 - 第二个元素:
1次 - 第三个元素:
2次 - …
- 第n个元素:
n-1次
总次数:
0+1+2+3+...+n-1 = n*(n-1)/2次所以最坏时间复杂度为:O(n^2)。
- 第一个元素:
-
最好时间复杂度:考虑数组原本是升序,那么所有元素需要移动或者比较的总次数为:
0+1+1+...+1 = n-1。所以最好时间复杂度为O(n)。 -
平均时间复杂度:O(n^2) ----> 算法不太行。
-
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:稳定,因为对于值相同的元素,后插入的时候不会插到相同元素的前面(
tmp >= arr[end]会break,即不插入)。
2、希尔排序
希尔排序详解
3、冒泡排序
3.1、算法思想
- 冒泡排序是通过对相邻元素的比较和位置交换,使得每次遍历都可以得到剩余元素中的最大值,将其放入有序序列中最终的位置,然后下一趟排序的时候就不用去比较这个已经确定了的元素。在冒泡排序中,会依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就如同水底下的气泡一样逐渐向上冒。
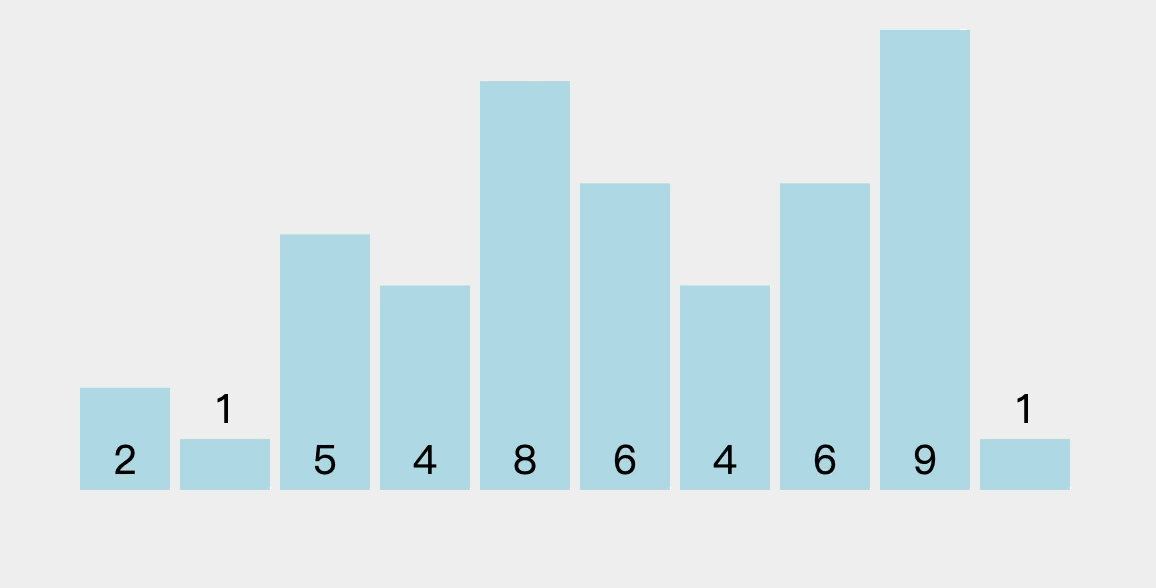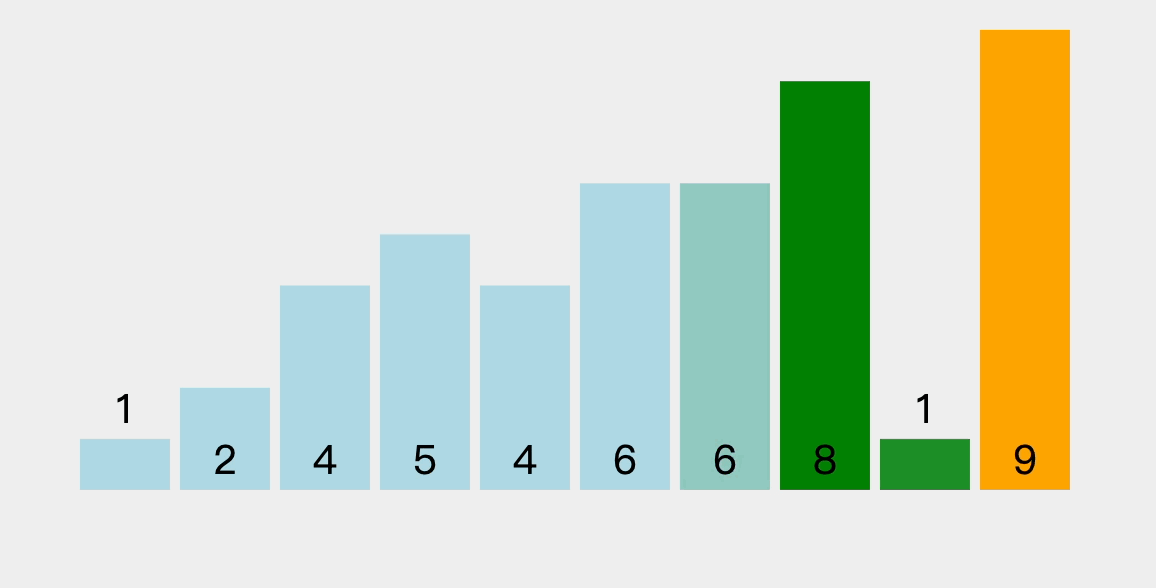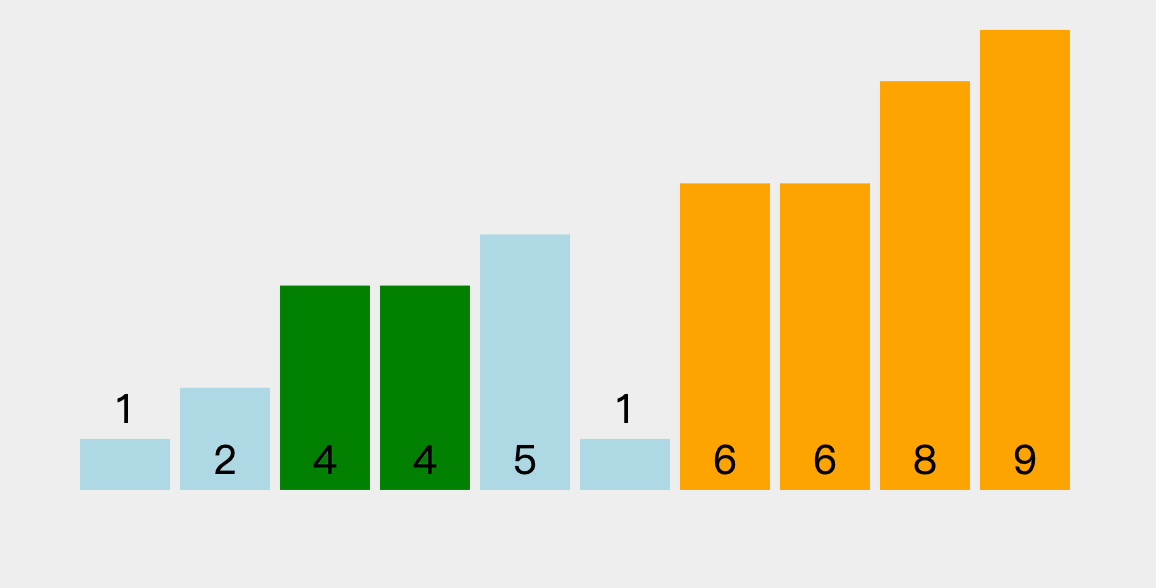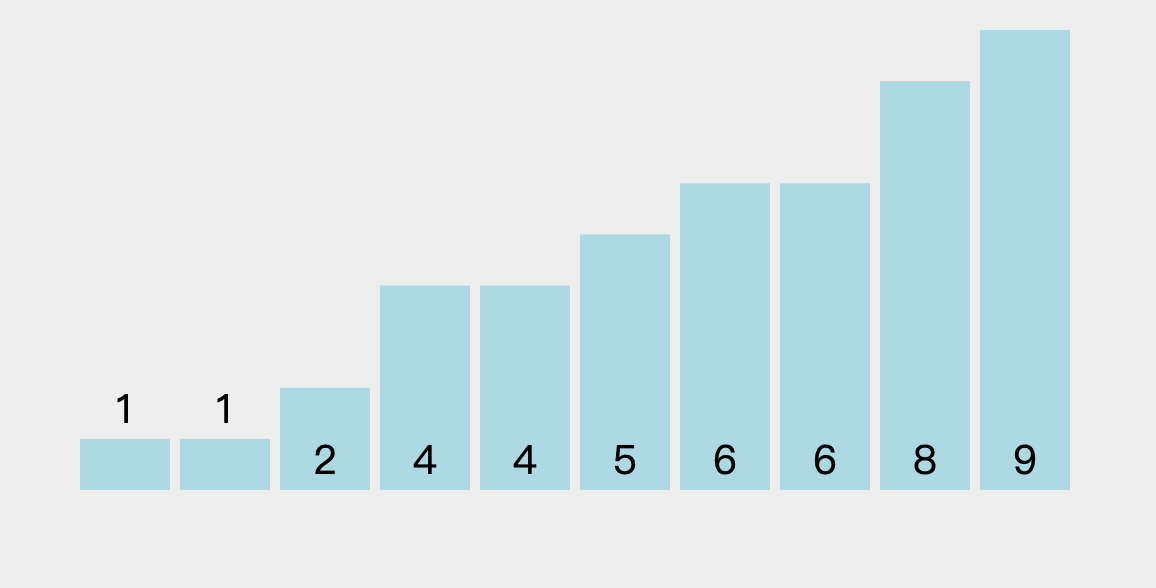
3.2、排序过程图解
-
每趟排序可以把一个元素”冒“到最终位置上,下一趟排序就可以少排序一个元素。


- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
3.3、排序代码
-
指针
i控制每趟需要少排序的元素个数(即已经有i个元素已经在最终位置上),指针j用来比较相邻元素的大小,若相邻元素是降序,则交换这两个元素。 -
这里定义了一个
flag,用来标记每趟排序是否有交换,如果有交换,就需要继续下一趟排序,没有交换则说明数组已经有序,那么就不用继续下一趟排序!void Swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; } //冒泡排序 void BubbleSort(int *arr, int n) { for (int i = 0; i < n; ++i) { int flag = 0; for (int j = 0; j < n - 1 - i; ++j) { if (arr[j + 1] < arr[j]) { flag = 1; Swap(&arr[j], &arr[j + 1]); } } if (flag == 0) { break; } } } -
时间复杂度计算:
-
最坏时间复杂度:考虑数组原本是降序,现在要求其升序。那么每个元素需要移动或者比较的次数为:
- 第一趟排序:
n-1次 - 第二趟排序:
n-2次 - 第三趟排序:
n-3次 - …
- 第n趟排序:
1次
总次数:
n-1+n-2+n-3+...+1 = n*(n-1)/2次所以最坏时间复杂度为:O(n^2)。
- 第一趟排序:
-
最好时间复杂度:考虑数组原本是升序。那么所有元素需要移动或者比较的次数为:
若不使用
flag:比较次数为n-1+n-2+n-3+...+1 = n*(n-1)/2次。使用
flag:比较次数为n-1次。 -
平均时间复杂度:O(n^2) —> 算法不太行。
-
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:稳定,因为对于值相同的元素,每一趟排序的时候不会交换(
arr[j + 1] < arr[j]才交换)。
4、(简单)选择排序
4.1、算法思想
- 选择排序是一种简单直观的排序算法。它的工作原理如下:(优化后的选择排序–>每次都能确定当前未排序序列的最小元素和最大元素的最终位置)
- 在未排序序列中找到最小元素和最大元素,最小元素存放到排序序列的起始位置,最大元素存放到排序序列的末尾位置。
- 再从剩余未排序元素中继续寻找最小元素和最大元素,然后最小元素放到前面已排序序列的末尾,最大元素放到后面已排序序列的前面。
- 以此类推,直到所有元素均排序完毕。
- 这里动画排序是每次选出一个最小值。(我们讲的算法更优哈哈)
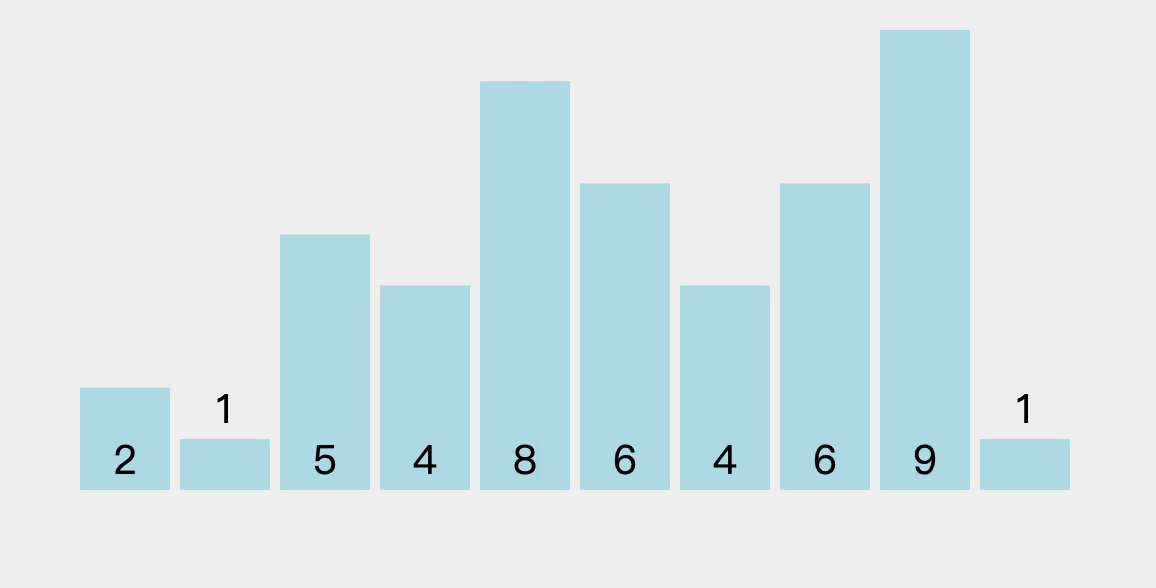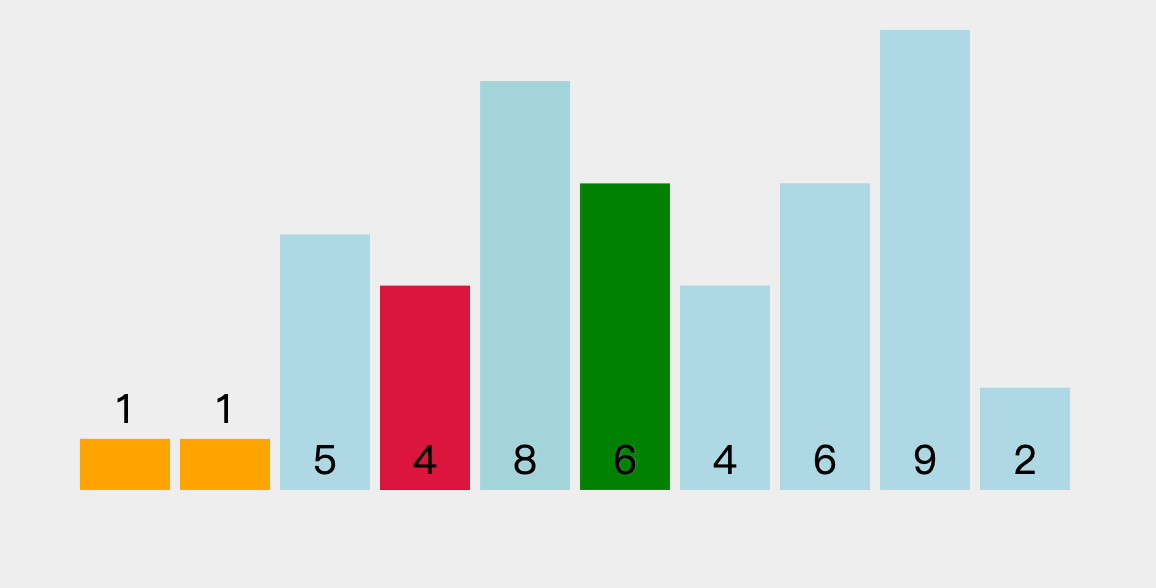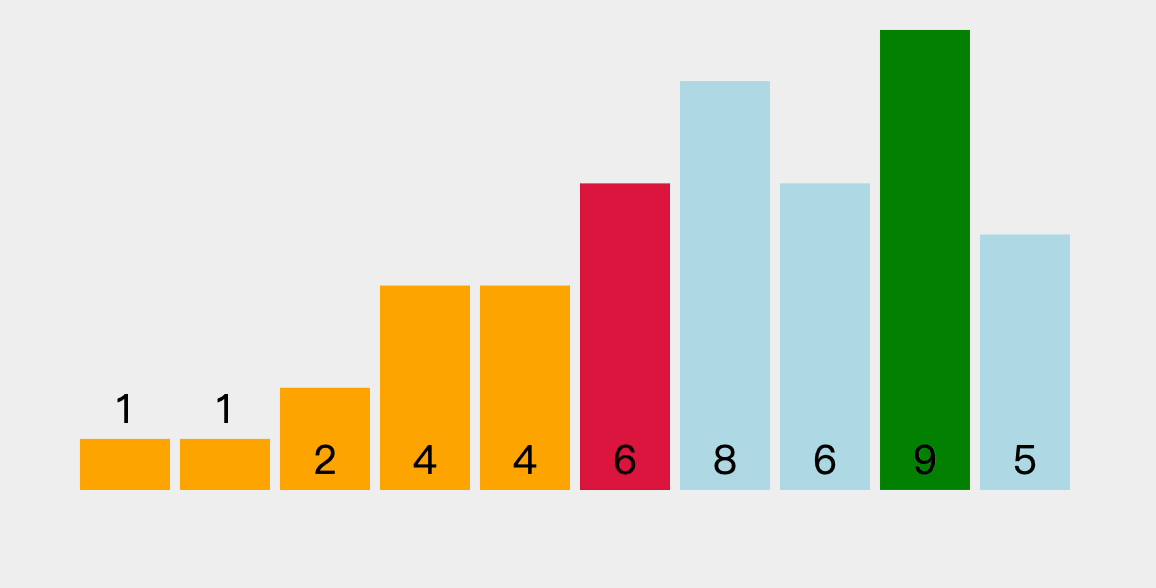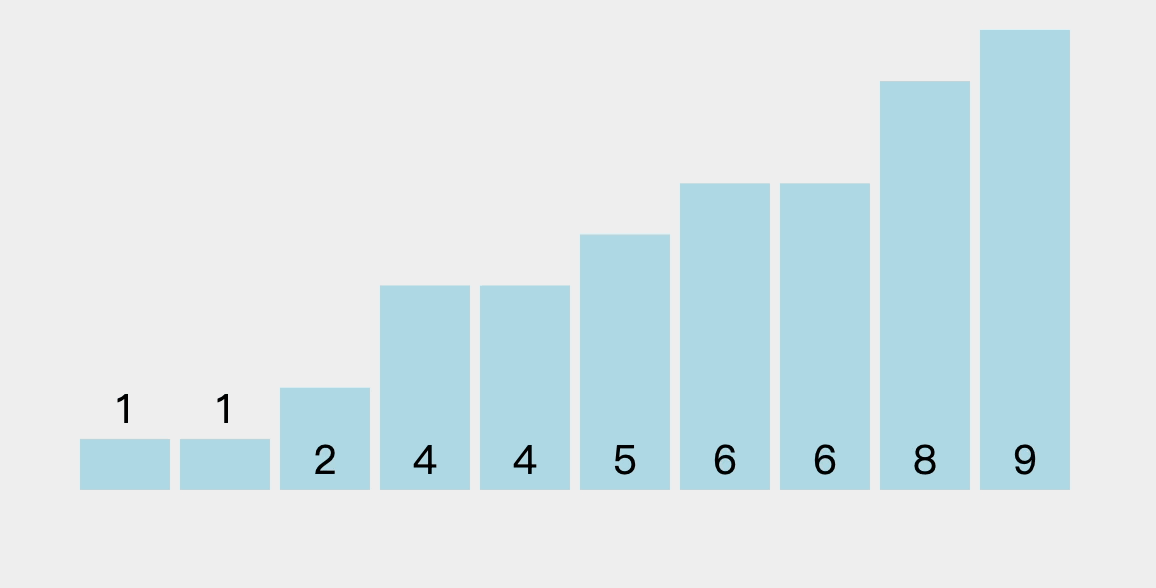
4.2、排序过程图解
-
在未排序序列中找到最小元素和最大元素,最小元素存放到排序序列的起始位置,最大元素存放到排序序列的末尾位置。

-
再从剩余未排序元素中继续寻找最小元素和最大元素,然后最小元素放到前面已排序序列的末尾,最大元素放到后面已排序序列的前面。
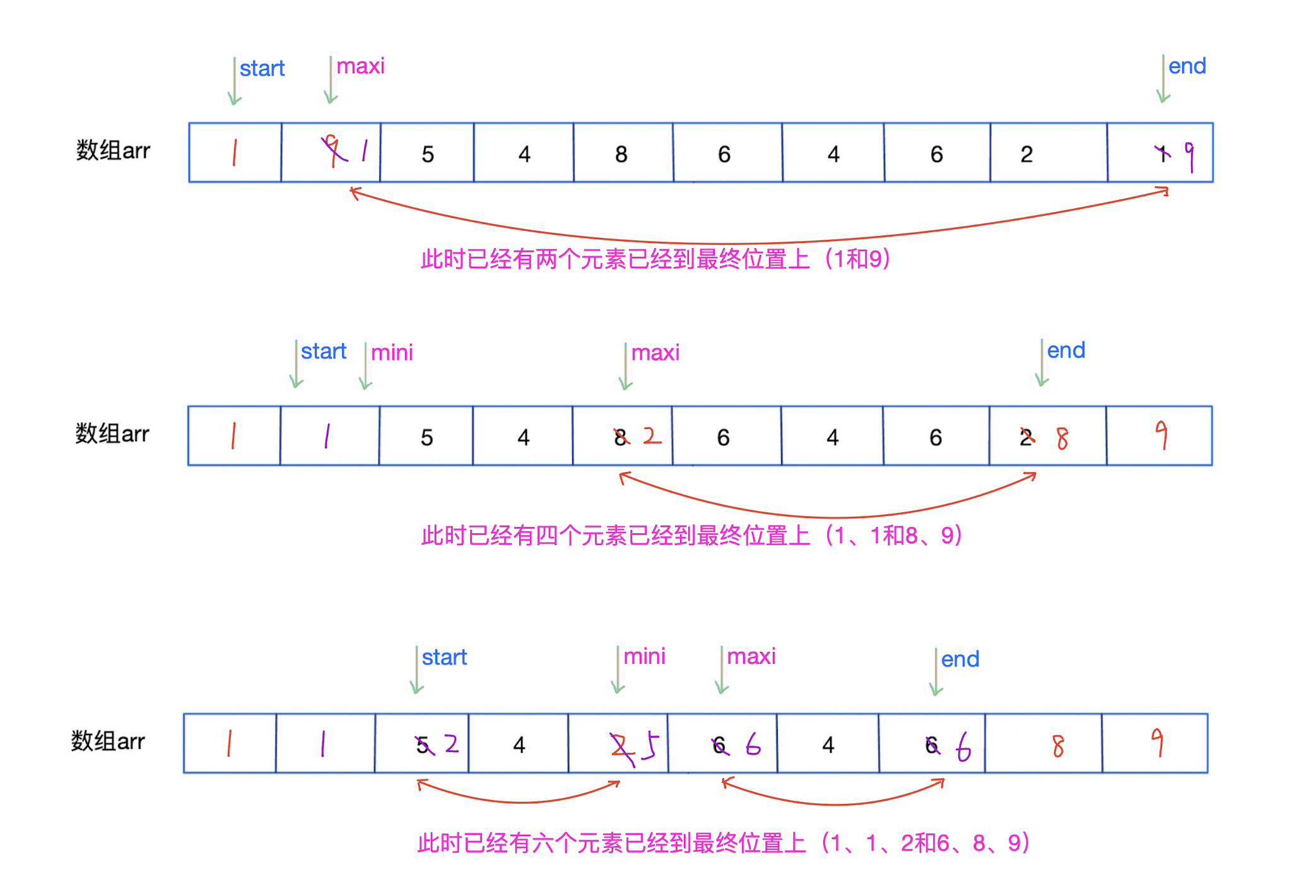
- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
-
以此类推,直到所有元素均排序完毕。
4.3、排序代码
-
使用
mini和maxi分别记录当前未排序的最小值下标和最大值下标在未排序的序列中找出最小值和最大值,然后分别交换到当前未排序的起始位置和末尾位置。需要注意的是:如果当前未排序的序列中,最大值刚好在未排序序列的起始位置,那么就需要记录好这个最大值与当前未排序的序列中的最小值交换后的位置,不记录的话,那么当前maxi指向的值不一定是最大值!//选择排序 void SelectSort(int *arr, int n) { int mini = 0; int maxi = 0; int start = 0; int end = n - 1; while (start < end) { for (int i = start + 1; i <= end; ++i) { if (arr[i] > arr[maxi]) { maxi = i; } if (arr[i] < arr[mini]) { mini = i; } } Swap(&arr[mini], &arr[start]); //注意此时如果start刚好是最大值的话,就会把最大值换走了,也就是本来最大值在 0 位置,交换后换到其他位置了,所以判断一下 if (start == maxi) { maxi = mini;//找到最大值的下标 } Swap(&arr[maxi], &arr[end]); //向中间靠拢 ++start; --end; } } -
时间复杂度计算:对于选择排序排序来说,没有什么最坏时间复杂度和最好时间复杂度,因为不管原数组起始是升序还是降序,元素之间的比较次数都是一样的:
- 确定了2个元素的最终位置:
n-1 - 确定了4个元素的最终位置:
n-1+n-3 - 确定了6个元素的最终位置:
n-1+n-3+n-5 - …
- 确定了n个元素的最终位置:
n+n-3+n-5+...+1 = n*(n+1)/4 <---大约,所以时间复杂度为O(n^2)。
- 确定了2个元素的最终位置:
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:不稳定,考虑序列(1,2,2),排序后序列为(1,2,2),我们发现
2的相对位置发生了变化,所以是不稳定的排序算法。
5、堆排序
堆排序详解
6、快速排序
快速排序递归方法和非递归方法详解
7、归并排序
快速排序递归方法和非递归方法详解
8、计数排序
8.1、算法思想
-
计数排序就是使用一个临时数组来记录这个原数组的元素对应这个临时数组下标出现的次数,然后再对这个临时数组从
0开始往后按下标出现的次数遍历。 -
优化:对于原数组最小值较大的情况,我们可以使用对这个临时数组进行==重定位==。
-
重定位:相当于计算机组成原理里面的将逻辑地址转化为物理地址的过程,比如序列
110,110,111,120,125,122,115,118,112,118,其实它的范围就是在110~125,区间长度为16,如果我们按照这个序列的最大值来建立数组,那么需要长度为126的数组,但是这个数组的前110个空间都是0,也就是并没有用上,浪费了。但是如果创建一个长度为16的数组,下标为0~15(原数组每个元素减110,这个110是这个原数组的最小值),是不是就可以匹配这个序列的范围了呢?那么问题是之后遍历这个临时数组,只能得到
0~15的下标,并不是我们要的110~125!其实,在遍历这个临时数组的时候,可以继续使用重定位,把这个0~15的下标重定位到110~125(每个下标都加110,这个110是这个原数组的最小值)!
-

8.2、排序过程图解
-
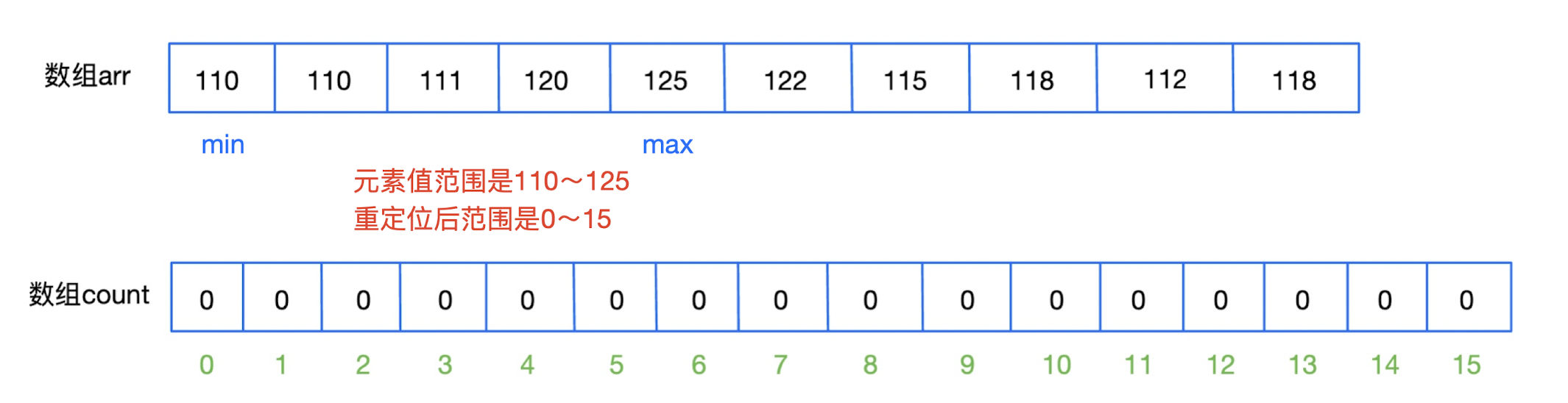
先找到原数组的最大值和最小值,然后就可以确定临时数组的长度,然后初始化这个临时数组(全
0)。
-
然后依次遍历原数组,根据重定位,将原数组的元素减去最小值去对应临时数组的下标,并对这个下标里的元素
+1。
-
遍历这个临时数组,对每个下标进行遍历,按下标对应的元素值看需要对此下标遍历几次(需要重定位回去—加上原数组的最小值)。

8.3、排序代码
-
用
min和max记录原数组的最小值和最大值,确定临时数组的长度(max-min+1),然后对临时数组count进行初始化,接下来就是把原数组里的元素重定位为临时数组的下标(元素值减原数组的最小值),并对此下标对应的元素+1,一直到遍历完原数组。 -
遍历这个临时数组
count,对每个下标进行遍历,按下标对应的元素值看需要对此下标遍历几次(需要重定位回去—加上原数组的最小值)。 -
注意:这里不能找最大最小值的下标,因为在重定位回去的时候
arr[j++]在变,也就是最小值下标不一定对应到最小值了!//计数排序 void CountSort(int *arr, int n) { //先找出数组的最大最小值 int max = arr[0]; int min = arr[0]; for (int i = 1; i < n; ++i) { if (arr[i] > max) { max = arr[i]; } if (arr[i] < min) { min = arr[i]; } } //节省空间,需要对元素重定位 int capacity = max - min + 1;//元素大小区间 //记录每个元素的出现次数 int *count = (int *) malloc(sizeof(int) * capacity); if (count == NULL) { perror("malloc error"); exit(-1); } memset(count, 0, sizeof(int) * capacity); for (int i = 0; i < n; ++i) { count[arr[i] - min]++; } int j = 0; for (int i = 0; i < capacity; ++i) { while (count[i]--) { arr[j++] = i + min; } } free(count); } -
时间复杂度计算:这里找最大值最小值花费时间
n,遍历临时数组花费时间k(临时数组长度),所以时间复杂度为O(n+k)。 -
空间复杂度计算:使用了临时数组(临时数组长度为k),所以空间复杂度为O(k)。
-
算法稳定性:稳定,因为它是利用一个数据的索引来记录元素出现的次数,而这个数组的索引就是元素的数值。当计数排序完成后,具有相同数值的元素在数组中的位置也相同,因此它们的顺序保持不变。
八大排序算法整体的时间复杂度、空间复杂度、算法稳定性等看如下表格:
排序算法 平均时间复杂度 最好情况 最坏情况 空间复杂度 排序方式 稳定性 (直接)插入排序 O(n^2) O(n) O(n^2) O(1) 内部排序 稳定 希尔排序 O(n^1.3) O(n^1.3) O(n^1.3) O(1) 内部排序 不稳定 冒泡排序 O(n^2) O(n) O(n^2) O(1) 内部排序 稳定 (简单)选择排序 O(n^2) O(n^2) O(n^2) O(1) 内部排序 不稳定 堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 内部排序 不稳定 快速排序 O(nlogn) O(nlogn) O(n^2) O(logn) 内部排序 不稳定 归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 外部排序 稳定 计数排序 O(n+k) O(n+k) O(n+k) O(k) 外部排序 稳定
OKOK,八大排序算法就到这里。如果你对Linux和C++也感兴趣的话,可以看看我的主页哦。下面是我的github主页,里面记录了我的学习代码和leetcode的一些题的题解,有兴趣的可以看看。
Xpccccc的github主页