递归：如何用三行代码找到“最终推荐人”？

文章来源于极客时间前google工程师−王争专栏。

推荐注册返佣金。用户A推荐用户B，用户B又推荐了用户C来注册。用户C的“最终推荐人”为用户A，用户B的“最终推荐人”也为用户A，而用户A没有“最终推荐人”。

可以通过数据库来记录这种推荐关系。

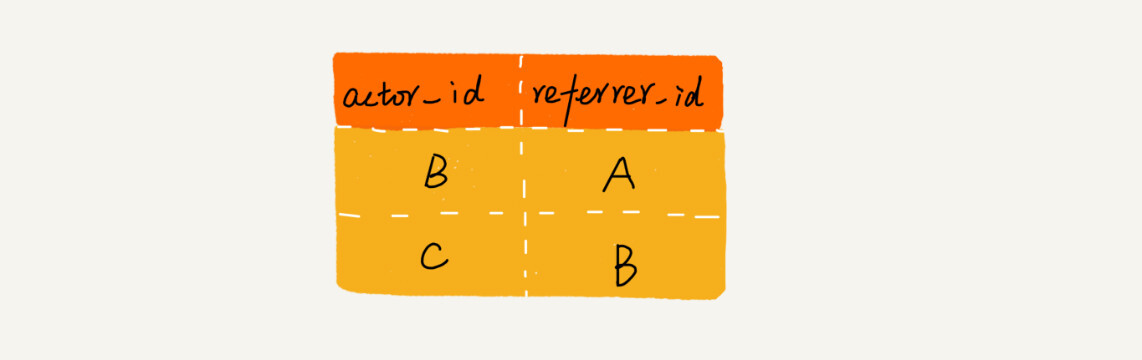
问题：给定一个用户ID，如何查找这个用户的“最终推荐人”？

如何理解“递归”？

递归应用：

DFS深度优先搜索
前中后序二叉树遍历

场景：周末带女朋友去电影院看电影，想知道自己坐在哪一排。

问题传递出去，直到第一排的人将信息传回来，直到前面的人告诉自己在哪一排，就直到答案了。

递归求解问题的过程，去的过程叫“递”，回来的过程叫“归”。基本上，所有的递归问题都可以用递推公式来表示。电影院看电影的例子，可以用递推公式表示为：

f(n) = f(n-1)+1 其中f(1) = 1

f(n)表示你想知道自己在哪一排
f(n-1)表示前面一排所在的排数
f(1) = 1表示第一排的人知道自己在第一排。

根据递推公式，代码实现如下：

public int f(int n){
    if(n == 1){ return 1;}
    return f(n-1)+1;
}

递归满足的三个条件

1.一个问题的解可以分解为几个子问题的解

子问题就是数据规模更小的问题。“自己在哪一排”的问题可以分解为“前一排的人在哪一排”这样一个子问题。

2.这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样

求解“自己在哪一排”的思路，和前面一排的人求解“自己在哪一排”的思路，是一模一样的。

3.存在递归的终止条件

不能无限分解为子问题，不能存在无限循环，这就需要有终止条件。f(1) = 1，这就是递归的终止条件。

如何编写递归代码？

关键是写出递推公式，找到终止条件，将递推公式转化为代码就简单了。

例题：假如这里有n个台阶，每次你可以跨1个或者2个台阶，请问走这n个台阶有多少种走法？如果有7个台阶，可以2，2，2，1或者1，2，1，1，2走上去，走法很多，如何用编程求得总共有多少种走法呢？

思路：可以将第一步的走法分为两类，第一类是第一步走了1个台阶，另一类是第一步走了2个台阶。所以n个台阶的走法就等于先走1阶后，n-1个台阶的走法，加上先走2阶后，n-2个台阶的走法，用公式表示就是：

f(n) = f(n-1)+f(n-2)

有了递推公式，递归代码基本上就完成了一半。接下来是终止条件。当有一个台阶时，我们不需要再继续递归，就只有一种走法。所以f(1) = 1。这个递归条件足够吗？我们可以用n=2,n=3这样比较小的数试验一下。

n=2时，f(2) = f(1)+f(0)。如果递归条件只有一个f(1) = 1那么f(2)就无法求解了。所以还要有f(0)=1，表示走0个台阶有一种走法，不过这样不符合正常的逻辑思维。所以我们把f(2)=2作为一种终止条件，表示走2个台阶有两种走法，一步走完或者分两步来走。

所以递归终止条件就是f(1)=1,f(2)=2。

将递推公式和终止条件实现为代码如下：

int f(int n){
    if(n == 1) return 1;
    if(n == 2) return 2;
    return f(n-1)+f(n-2);
}

总结：写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

屏蔽掉递归细节，理解就会简单。编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑取分解递归的每个步骤。

递归代码警惕堆栈溢出

堆栈溢出会造成系统性崩溃，后果非常严重。为什么递归代码容易造成堆栈溢出呢？如果预防？

函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

如果将系统栈或者jvm堆栈大小设置为1KB，电影院的例子中，在求解f(19999)时会出现堆栈报错：

Exception in thread "main" java.lang.StackOverflowError

可以通过限制递归调用最大深度的方式来解决堆栈溢出。递归调用超过一定深度（比如1000）之后，我们就不继续往下再递归了，直接返回报错。伪代码如下：

//全局变量，表示递归的深度
int depth = 0;

int f(int n){
    ++depth;
    if(depth > 1000){throw exception;}
    if(n == 1){return 1;}
    return f(n-1)+1;
}

但是这种做法并不能完全解决问题，因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，事先无法计算。计算过于复杂，影响代码可读性。所以如果最大深度比较小，比如10、50，就可以用这种方法，否则这种方法并不是很实用。

递归代码要警惕重复计算

台阶例子中，将整个递归过程分解一下，如图所示：

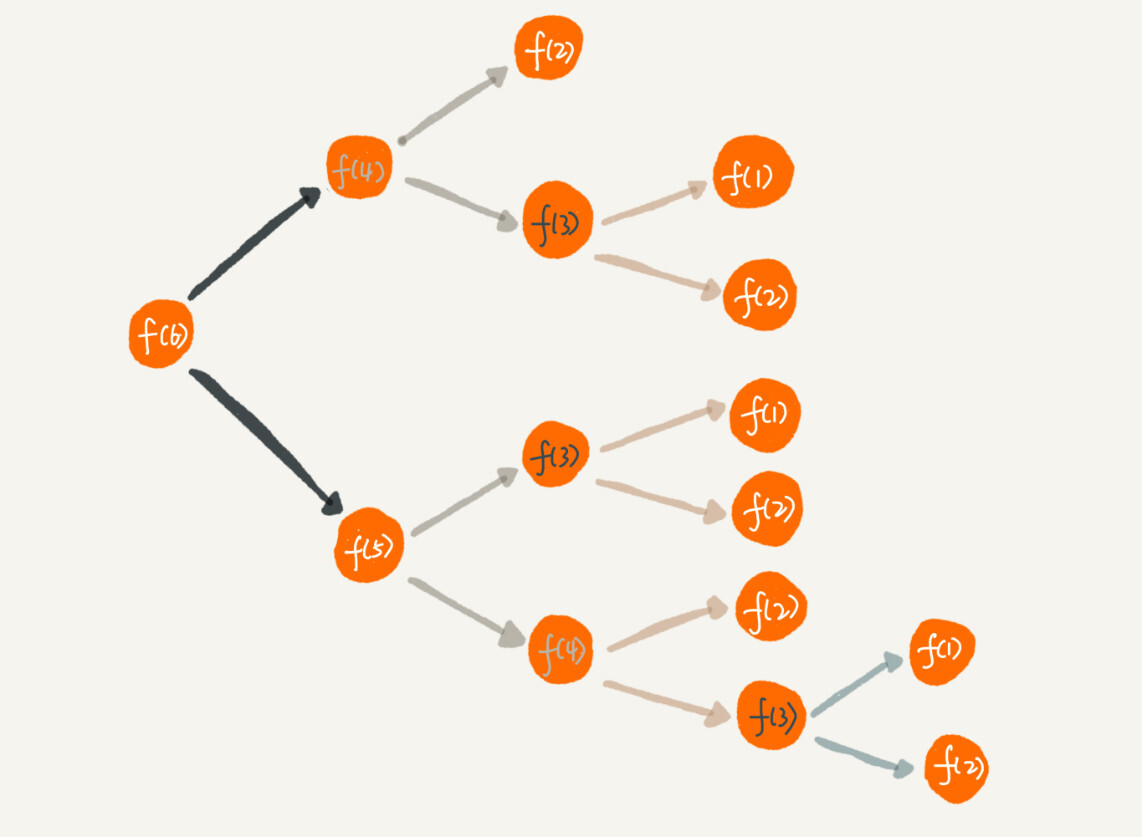
如上图所以f(3)被重复计算了很多次，这就是重复计算问题。

为了避免重复计算，我们可以通过一个数据结构（比如散列表）来保存已经求解过的f(k)。当递归调用到f(k)时，先看下是否已经求解过了，如果是，则直接从散列表中取值返回，不重复计算，这样就能避免重复计算问题。

改造代码如下：

public int f(int n){
    if(n == 1) return 1;
    if(n == 2) return 2;
    if(hasSolvedList.containsKey(n)){
        return hasSolvedList.get(n);
    }
    int ret = f(n-1)+f(n-2);
    hasSolvedList.put(n,ret);
    return ret;
}

时间效率上，递归代码里多了很多函数调用，当这些函数调用的数量较大时，就会积聚成一个可观的时间成本。

空间复杂度上，因为递归调用一次就会在内存栈中保存一次现场数据，所以分析递归代码空间复杂度时，需要额外考虑这部分的开销。比如电影院例子，空间复杂度不是O(1)，而是O(n)。

如何将递归代码改写为非递归代码

电影院例子，抛开场景，只看f(x) = f(x-1)+1

int f(n){
    int ret = 1;
    for(int i=2;i<=n;++i){
        ret = ret + 1;
    }
    return ret;
}

同样第二个例子也可以改为非递归的实现方式。

int f(int n){
    if(n == 1) return 1;
    if(n == 2) return 2;
    
    int ret = 0;
    int pre = 2;
    int prepre = 1;
    for(int i=3;i<=n;++1){
        ret = pre+prepre;
        prepre = pre;
        pre = ret;
    }
    return ret;
}

所有的递归代码都可以改为这种迭代循环的非递归写法。递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身提供的，我们没有感知罢了。如果我们自己在内存堆上实现栈，手动模拟入栈、出栈过程，这样任何递归代码都可以改写成看上去不是递归代码的样子。

但是这种思路实际上是将递归改为了“手动”递归，本质并没有改变，而且也并没有解决前面讲到的某些问题，徒增了实现复杂度。

解答开篇

如何找到“最终推荐人”

long findRootReferrerId(long actorId) {
  Long referrerId = select referrer_id from [table] where actor_id = actorId;
  if (referrerId == null) return actorId;
  return findRootReferrerId(referrerId);
}

上面的代码并不能工作，为什么？

第一，如果递归很深，可能会有堆栈溢出的问题。

第二，如果存在脏数据，会发生死循环。

第二个问题可以用限制递归深度来解决，更好的方式是自动检测A-B-C-A这种“环”的存在。（如何实现？）