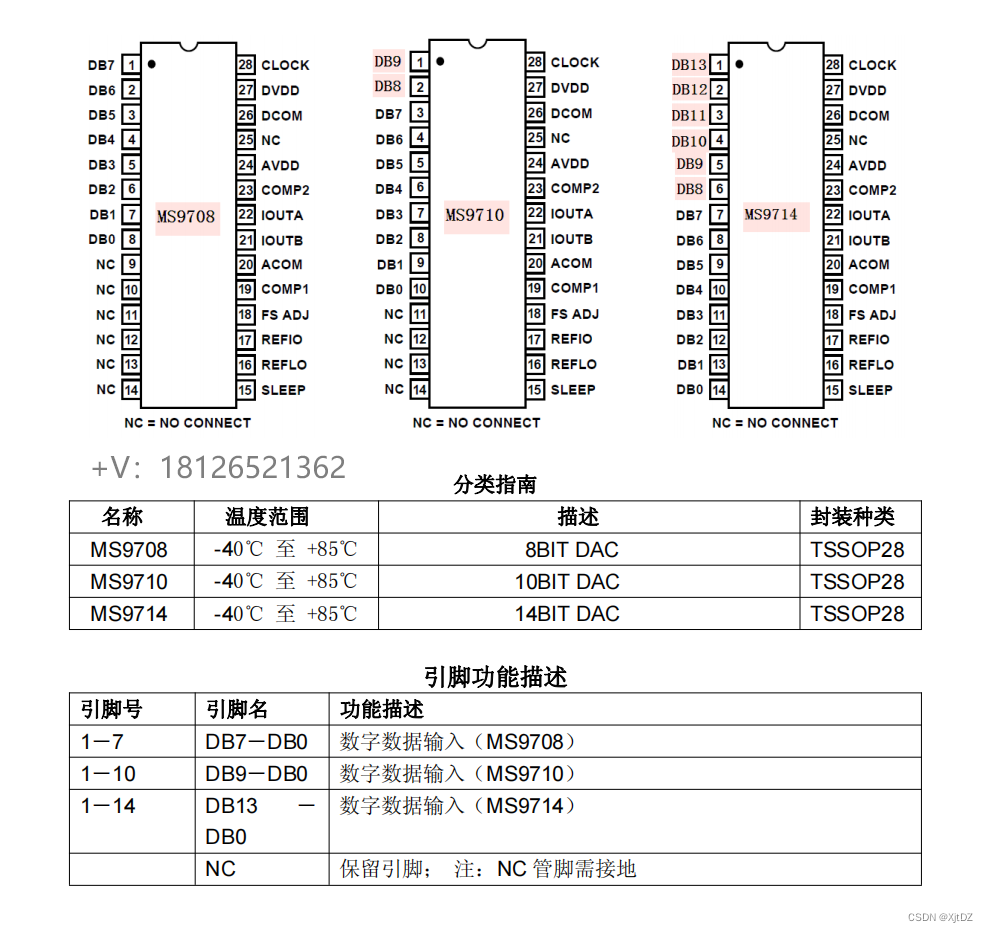
一、箱形图的介绍
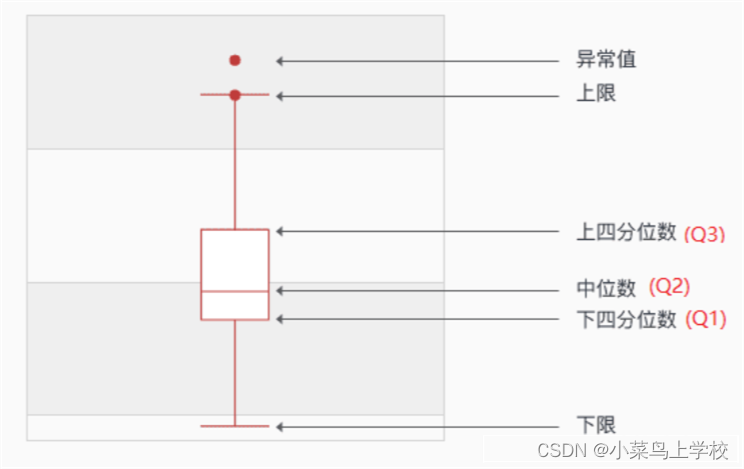
箱形图又称为盒须图、盒式图、盒状图或箱线图，是一种用作显示一组数据分散情况的统计图，因型状如箱子而得名。它是利用数据中的五个统计量：最小值、上四分位数、中位数、下四分位数与最大值来描述数据的一种统计图。
箱形图主要是为了检测异常值，箱形图最大的优点就是不受异常值的影响，它能够直观地显示数据的异常值，分布的离散程度以及数据的对称性，同时也利于数据的清洗。
二、箱形图五要素
箱型图五要素包括异常值、 上限、下限、上四分位（Q3)、下四分位（Q1）和中位数（Q2）。借助其它博主的例子，有有序序列一个test = c(1,2,3,4,5,6,7,8)来说明问题。
（1）中位数
中位数，即二分之一分位数，等于该样本中所有数值由小到大排列后第50%的数字。所以计算的方法就是将一组数据平均分成两份，取中间这个数。
如果原始序列长度n是奇数，那么中位数所在位置是(n+1)/2；如果原始序列长度n是偶数，那么中位数所在位置是n/2，n/2+1，中位数的值等于这两个位置的数的算数平均数。
（2）下四分位数Q1
强调一下，四分位数的求法，是将序列平均分成四份。等于该样本中所有数值由小到大排列后第25%（四分之一）的数字。具体的计算目前有(n+1)/4与(n-1)/4两种，一般使用(n+1)/4。有序序列一个test = c(1,2,3,4,5,6,7,8)，通过summary(test)来获取test这个序列的中位数，上四分位数，下四分位数以及算数平均值。
这个Q1=2.75是怎么计算出来的呢？首先序列长度n=8，(1+n)/4=2.25，这是什么意思呢？说明上四分位数在第2.25个位置数，实际上这个数是不存在的，但我们知道这个位置是在第2个数与第3个数之间的。只能假想从第2个数到第3个数之间是均匀分布的。那么第2.25个数就是第二个数*0.25+第三个数*0.75，即2*0.25+3*0.75=0.5+2.25=2.75。
（3）上四分位数Q3
四分位数的求法，是将序列平均分成四份。等于该样本中所有数值由小到大排列后第75%（四分之三）的数字，这个下四分位数所在位置计算方法同上，只不过是(1+n)/4*3=6.75，乘以这个3表示是四分之三的位置，这个6.75是个介于第六个位置与第七个位置之间的地方。对应的具体的值是0.75*6+0.25*7=6.25。
（4）上限
上限是非异常范围内的最大值。首先要知道什么是四分位距如何计算的？四分位距（interquartile range, IQR），又称四分差。四分位距IQR=Q3-Q1，那么上限=Q3+1.5IQR
IQR=Q3-Q1 本例中IQR=6.25-2.75=3.5
上限=Q3+1.5IQR 本例中 上限=6.25+1.5*3.5=11.5 与剔除异常值后的极大值8，两者取最小值，所以本例中的上限即为 8 。
（5）下限
下限是非异常范围内的最小值。下限=Q1-1.5IQR
本例中 下限=6.25-1.5*3.5=1 剔除两个异常值后的极小值1，所以本例中的下限即为 1 。
（6）异常值
在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值（extreme outliers）。
三、箱型图的特征
（1）直观地观察到异常值，如果数据存在离群点，即位于上下边缘区域之外，以圆点的形式表示；
（2）当箱型图很短时，意味着很多数据多集中分布在很小的范围内；
（3）当箱型图很长时，意味着数据分布比较离散，数据间的差异比较大；
（4）当中位数接近底部时，说明大部分的数据值比较小；
（5）当中位数接近顶部时，说明大部分的数据值比较大；
（6）中位数所处的高低位置能反映数据的偏斜程度；
（7）如果上下虚线比较长，说明上下四分位数之外的数据变化比较大，整体数据的方差和标准偏差也比较大；
（8）箱型图的上下边缘并非最大值或最小值。
四、箱型图的缺点
（1）箱型图虽然能显示出数据的分布偏态，但是不能提供关于数据分布偏态和尾重程度的精确度量；
（2）对于批量较大的数据批，箱线图反映的形状信息更加模糊；
（3）用中位数代表总体平均水平有一定的局限性。
所以，应用箱线图最好结合其它描述统计工具如均值、标准差、偏度、分布函数等来描述数据批的分布形状。
部分内容转自：一文看懂数据分析各种图形（箱型图、数据分布图、线性回归图、相关关系图）（阿里天池）-CSDN博客
https://blog.csdn.net/tangxianyu/article/details/124210558?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169720098616800226549041%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169720098616800226549041&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~baidu_landing_v2~default-4-124210558-null-null.nonecase&utm_term=%E7%AE%B1%E5%BD%A2%E5%9B%BE&spm=1018.2226.3001.4450
