1.最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。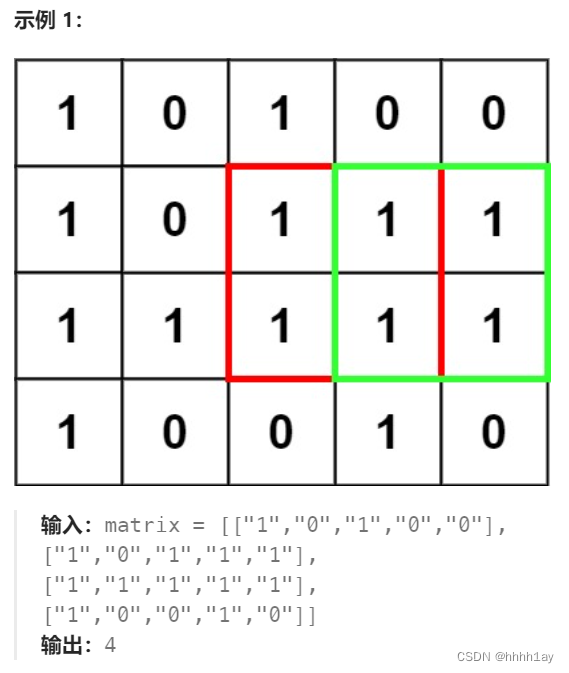

方法一：动态规划 

#方法一：动态规划
def maximalSquar(matrix):
    dp=[[0]*(len(matrix[0])+1) for i in range(len(matrix)+1)] #dp[i][j] 表示以该位置为右下角的能构成的最大正方形
    res=0
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            if matrix[i][j]=='1':
                dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1 #状态转移方程,求可能的最大边长，要考虑限制条件
            res=max(res,dp[i][j])
    return res*res

2.为运算表达式设计优先级 

给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。

生成的测试用例满足其对应输出值符合 32 位整数范围，不同结果的数量不超过 104 。

方法一：递归+分冶 

#方法一：递归+分冶
def diffWaysToCompute(expression):
    if expression.isdigit():
        return [int(expression)] #是数字则返回数字
    res=[] #保存结果
    for i in range(len(expression)):
        if expression[i] in ['+','-','*']: 
            left=diffWaysToCompute(expression[:i]) #递归，分成左右两边求解两边可能的结果
            right = diffWaysToCompute(expression[i + 1: ])
            for l in left:
                for r in right:
                    if expression[i]=='+':
                        res.append(l+r)
                    elif expression[i]=='-':
                        res.append(l-r)
                    elif expression[i]=='*':
                        res.append(l*r) #两边可能的组合
    return res

3.丑数 II 

给你一个整数 n ，请你找出并返回第 n 个 丑数 。

丑数 就是只包含质因数 2、3 和/或 5 的正整数。

方法一：三指针 

#方法一：三指针
def nthUglyNumber(n):
    res,a,b,c=[1 for i in range(n)],0,0,0
    for i in range(1,n):
        x1,x2,x3=res[a]*2,res[b]*3,res[c]*5  #等于前面的丑数*2/3/5
        res[i]=min(x1,x2,x3)      #当前位置的丑数比前一个丑数大的最小的丑数
        if res[i]==x1:
            a+=1    #指针移动，避免重复
        if res[i]==x2:
            b += 1
        if res[i]==x3:
            c+=1
    return res[-1]