Tag

【哈希表】【数组】

---

题目来源

1. 两数之和

---

题目解读

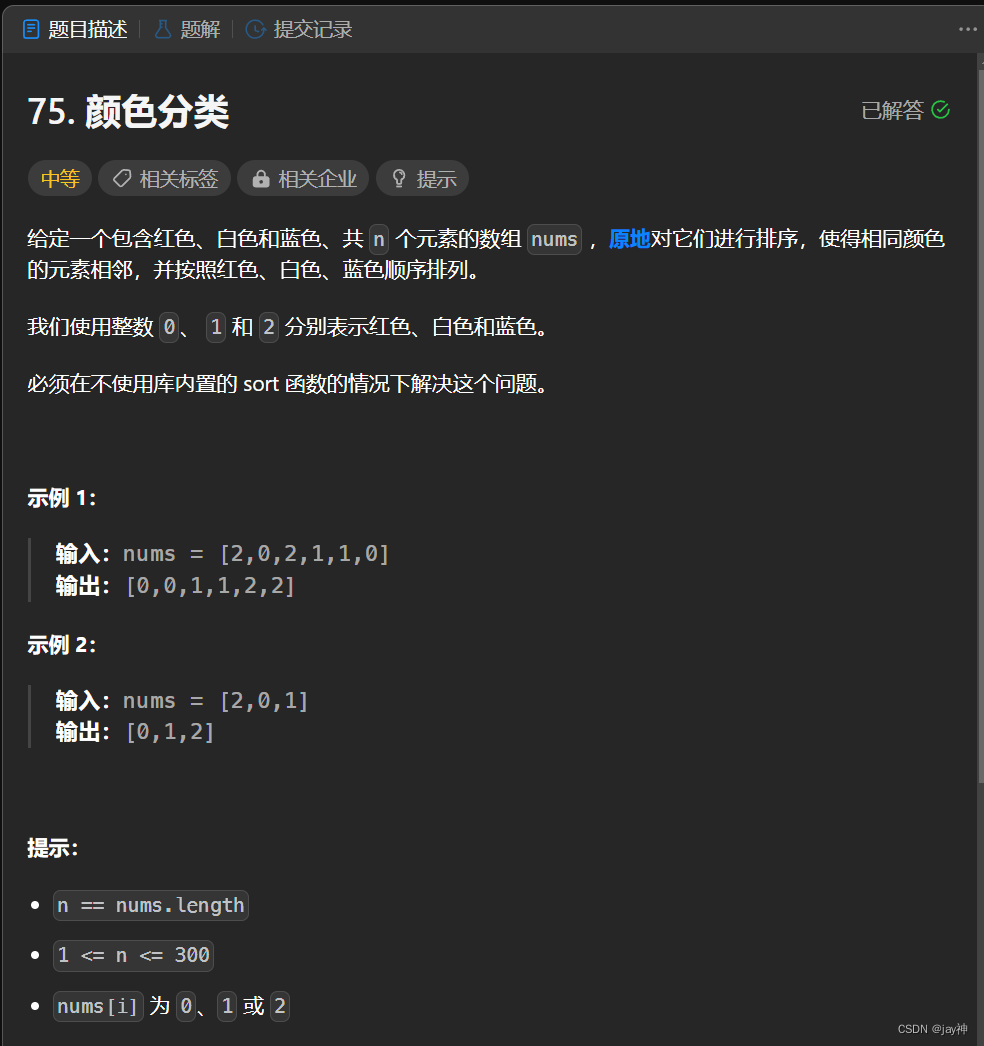
给定一个下标从 1 开始按照 非递减顺序排列 的整数数组 numbers，找出两数之和等于 target 的两个数，返回它们的下标，其中每个整数只能使用一次，题目保证只有唯一的答案。

---

解题思路

本题属于基础题，与 167. 两数之和 II - 输入有序数组 解法基本一致。现在有三种解法如下。

方法一：暴力枚举

一个比较容易想到的方法就是枚举所有可能的两数组合，使用两层枚举，第一层枚举第一个整数，第二层枚举第二个整数。本题的数据量为 $10^4$，两层枚举的时间复杂度为 $10^8$，勉强可以通过。

具体地，在枚举中判断两数之和是否等于 target，如果相等，直接返回对应的下标。

因为每个元素只可以使用一次，并且两数先后出现的顺序没有要求，因此
第二层枚举的整数可以从第一层枚举的整数的后一个位置开始。

实现代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        int i, j;
        for( i = 0; i < n - 1; i ++) {
            for( j = i + 1; j < n; j ++) {
                if(nums[i] + nums[j] == target) {
                    return {i,j};
                }
            }
        }
        return {i,j};
    }
};

复杂度分析

时间复杂度：$O(n^2)$。

空间复杂度：$O(1)$。

方法二：哈希表

方法一中的时间复杂度可以优化到 $O(n)$。

我们在枚举第二个整数的时候，可以事先用一个哈希表来记录下所有整数以及位置，这样枚举第二个整数的时间复杂度可以降为 $O(1)$，但是需要一个额外的空间。

具体地，可以先一次遍历 numbers，记录每个整数以及下标；记录完毕后，枚举第一个加数，在哈希表中查找第二个加数；以上的过程可以用一个循环就可以解决：枚举第一个加数之后，先在哈希表中查询有么有合适的第二个加数，然后再将当前的加数放入哈希表中，这样可以省去一次 for 循环。

实现代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        unordered_map<int, int> mp;
        for (int i = 0; i < n; ++i) {
            if (mp.find(target - nums[i]) != mp.end()) {
                return {i, mp[target - nums[i]]};
            }
            mp[nums[i]] = i;
        }
        return {-1, -1};
    }
};

复杂度分析

时间复杂度：$O(n)$，$n$ 为数组 numbers 的长度，只要一次循环就可以枚举两个加数。

空间复杂度：$O(n)$，记录整数以及位置所用的空间。

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 👍 哦。