654.最大二叉树
思路
最大二叉树的构建过程如下:

对于这道题,思路整体模仿的是昨天的 根据中后序遍历构造二叉树 的解题思路。
直接看代码:
class Solution {
//用于快速查找
private Map<Integer,Integer> map;
public TreeNode constructMaximumBinaryTree(int[] nums) {
if (nums.length == 0){
return null;
}
map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
map.put(nums[i],i);
}
return structTree(nums,0, nums.length - 1);
}
TreeNode structTree(int[] nums,int begin,int end){//左闭右闭
if (begin > end){
return null;
}
if (end - begin == 0){
return new TreeNode(nums[end]);
}
int val = Integer.MIN_VALUE;//保存当前最大值
int index;//保存当前最大值是索引值
for (int i = begin; i <= end; i++) {
val = val > nums[i] ? val : nums[i];
}
index = map.get(val);
TreeNode node = new TreeNode(val);//构建结点
node.left = structTree(nums,begin,index-1);
node.right = structTree(nums,index + 1, end);
return node;
}
}617.合并二叉树
思路
其实和遍历一个树逻辑是一样的,只不过传入两个树的节点,同时操作。
递归
二叉树使用递归,就要想使用前中后哪种遍历方式?
本题使用哪种遍历都是可以的。
我们下面以前序遍历为例。
动画如下:
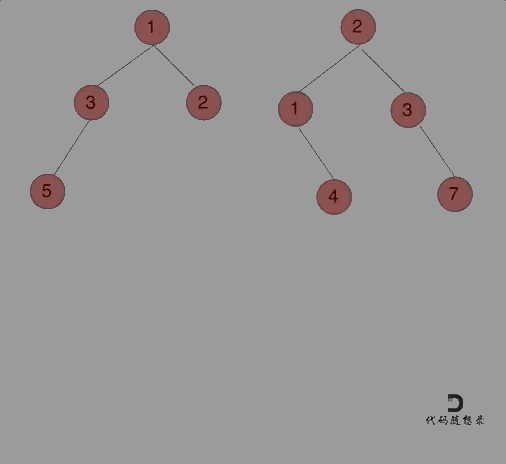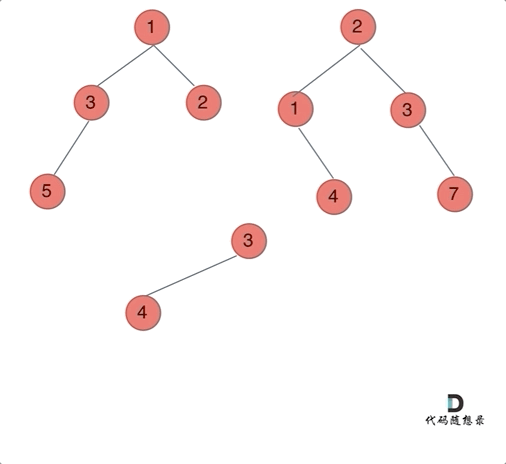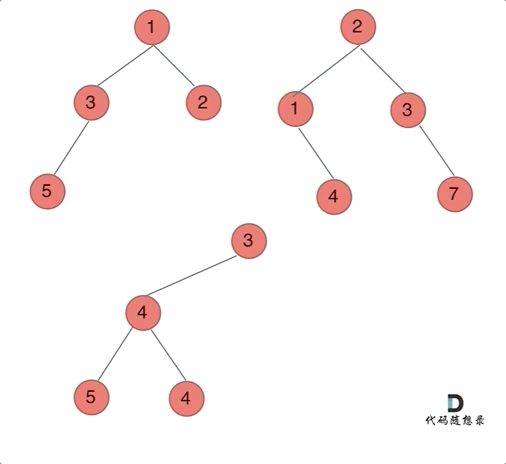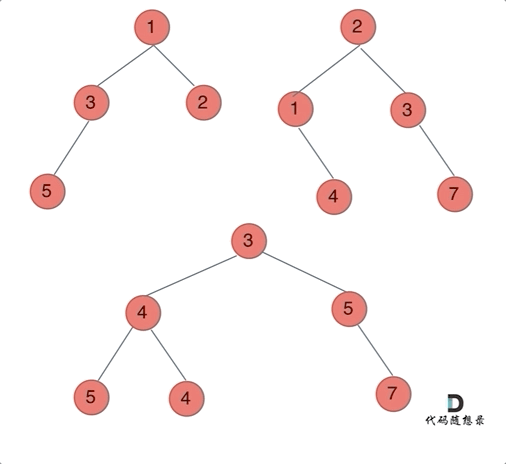
那么我们来按照递归三部曲来解决:
- 1.确定递归函数的参数和返回值:
首先要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点。
代码如下:
TreeNode structTree(TreeNode root1, TreeNode root2)
- 2.确定终止条件:
因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了(如果t2也为NULL也无所谓,合并之后就是NULL)。
反过来如果t2 == NULL,那么两个数合并就是t1(如果t1也为NULL也无所谓,合并之后就是NULL)。
代码如下:
if (root1 == null){return root2;} // 如果t1为空,合并之后就应该是t2
if (root2 == null){return root1;} // 如果t2为空,合并之后就应该是t1
- 3.确定单层递归的逻辑:
单层递归的逻辑就比较好写了,这里我们重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
那么单层递归中,就要把两棵树的元素加到一起。
root1.val += root2.val;接下来t1 的左子树是:合并 t1左子树 t2左子树之后的左子树。
t1 的右子树:是 合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点。
root1.left = structTree(root1.left,root2.left);
root1.right = structTree(root1.right,root2.right);
return root1;最终代码如下:
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
return structTree(root1,root2);
}
TreeNode structTree(TreeNode root1, TreeNode root2){
if (root1 == null){return root2;}
if (root2 == null){return root1;}
root1.val += root2.val;
root1.left = structTree(root1.left,root2.left);
root1.right = structTree(root1.right,root2.right);
return root1;
}
}700.二叉搜索树中的搜索
思路
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
这就决定了,二叉搜索树,递归遍历和迭代遍历和普通二叉树都不一样。
递归法
- 1.确定递归函数的参数和返回值
递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
代码如下:
TreeNode findNode(TreeNode node, int val)- 2.确定终止条件
如果root为空,或者找到这个数值了,就返回root节点。
if (node == null || node.val == val){return node;}
- 3.确定单层递归的逻辑
看看二叉搜索树的单层递归逻辑有何不同。
因为二叉搜索树的节点是有序的,所以可以有方向的去搜索。
如果 node.val > val,搜索左子树,如果node.val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL。
代码如下:
if (node.val > val){
return findNode(node.left, val);
}else {
return findNode(node.right, val);
}整体代码如下:
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
return findNode(root,val);
}
TreeNode findNode(TreeNode node, int val){
if (node == null || node.val == val){return node;}
if (node.val > val){
return findNode(node.left, val);
}else {
return findNode(node.right, val);
}
}
}98.验证二叉搜索树
思路
要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。【升序的】
有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。
递归法
具体看 代码随想录:验证二叉搜索树
最好再看一次视频便于理解 视频
代码:
class Solution {
TreeNode max;
public boolean isValidBST(TreeNode root) {
return isTree(root);
}
boolean isTree(TreeNode node){
if (node==null){return true;}
boolean left = isTree(node.left);
if (!left){return false;}
if (max != null && node.val <= max.val){
return false;
}
max = node;
return isTree(node.right);
}
}以上为我做题时候的相关思路,自己的语言组织能力较弱,很多都是直接抄卡哥的,有错误望指正。