---

链式二叉树

1. 概念

设计不同的节点结构可构成不同形式的链式存储结构。由二叉树的定义可知，二叉树的节点由一个数据元素分别指向其左右子树的两个分支构成，则表示二叉树的链表中的结点至少包含3个域：数据域和左右指针域，左右指针分别指向左右孩子所在的链节点的存储地址。

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

2. 链式二叉树的基本操作

前序遍历

前序遍历又叫先根遍历，先遍历根节点再遍历左子树和右子树，而左子树和右子树又有根节点，这就是一个递归操作。就是按根左右的遍历方法。

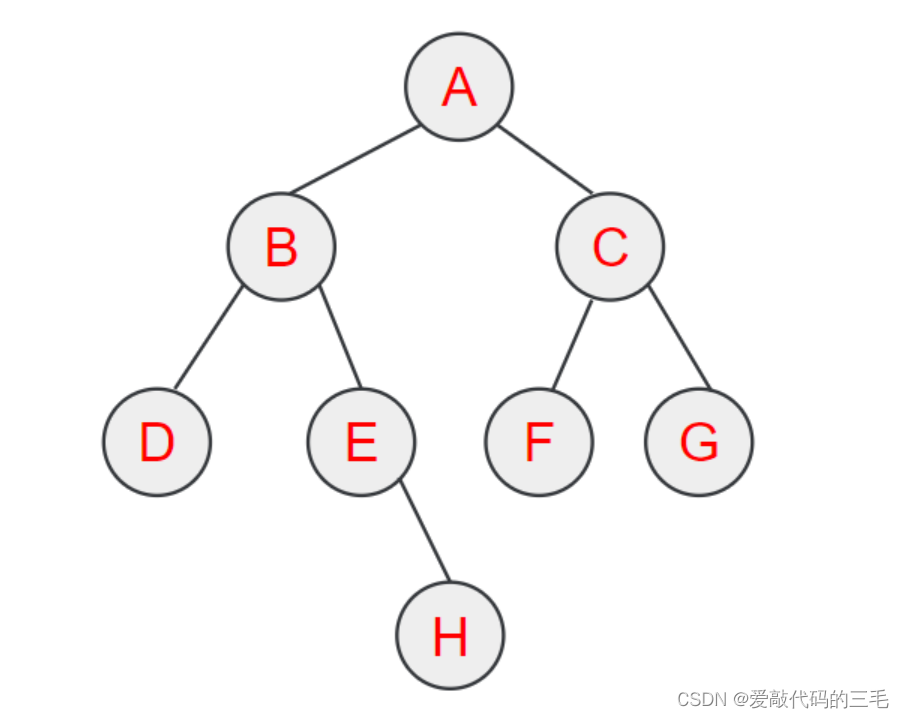
比如下面这棵数的前序遍历就是ABDEHCFG

// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);

}

中序遍历

中序遍历中根遍历，它的遍历顺序就是先遍历左子树再遍历根节点再遍历右子树，也就是左根右。

这棵树的中序遍历就是DBEHAFCG

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	
	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
}

后续遍历

后续遍历也叫后根遍历，遍历的顺序是先左子树再右子树最后根节点，按照左右根来遍历二叉树。

下面这棵树的后续遍历就是DHEBFGCA

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);
}

根据前序遍历构建二叉树

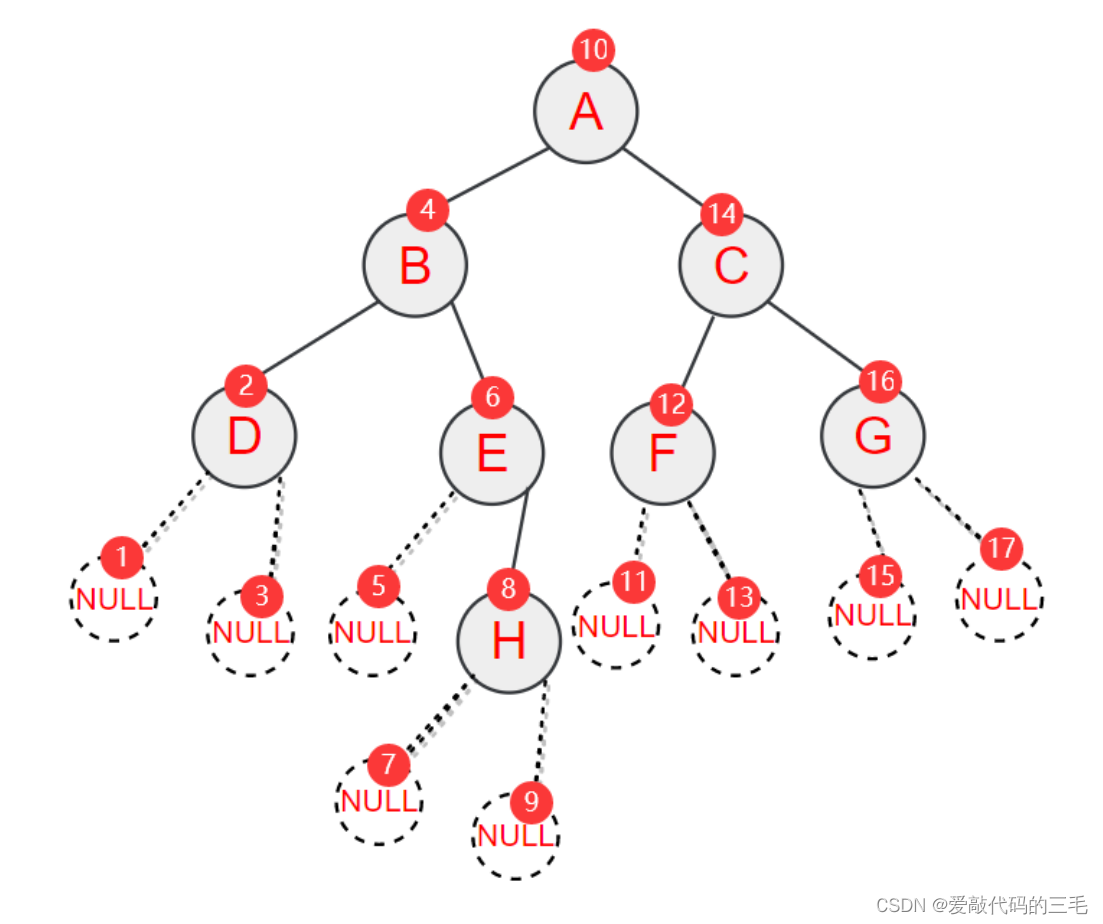
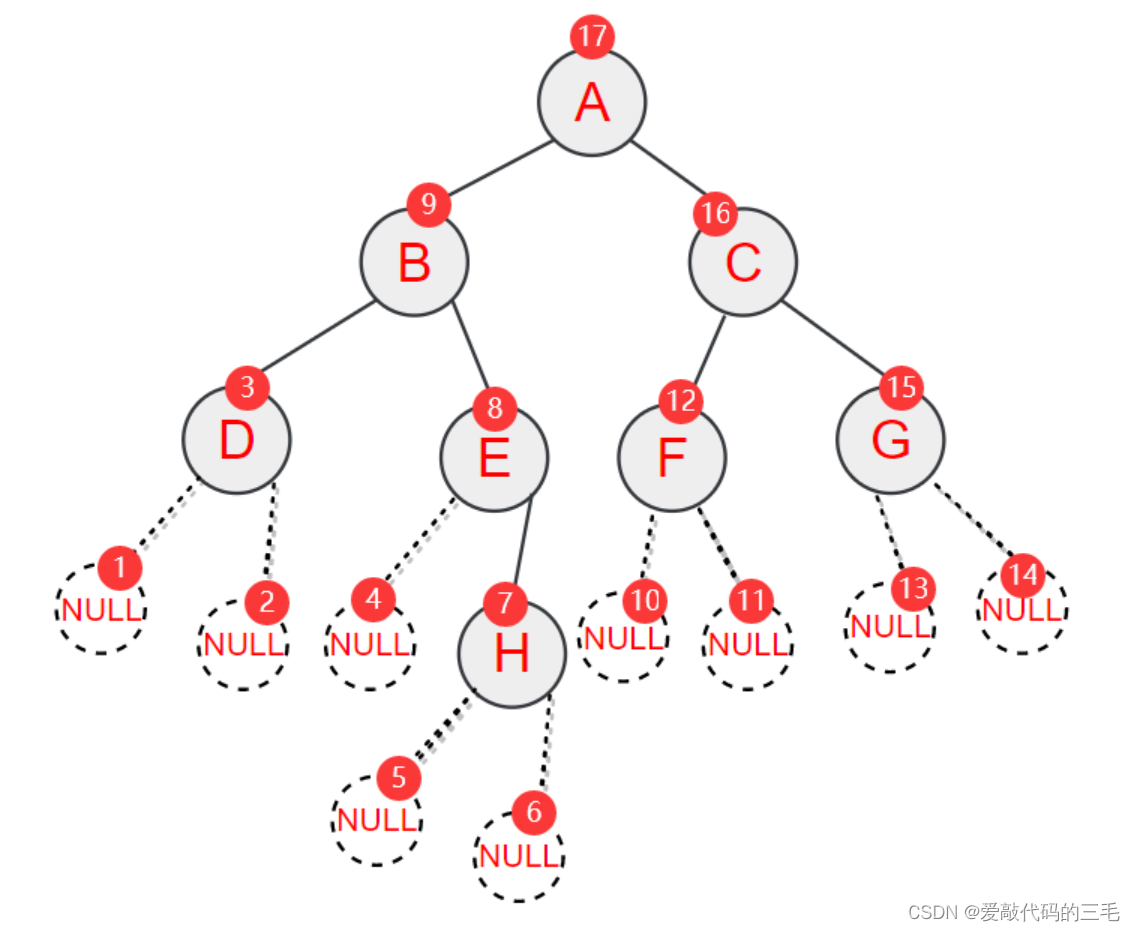
给定一个字符串。是二叉树树的前序遍历ABD##E#H##CF##G##，其中#代表NULL，通过这个字符串构造一颗二叉树。

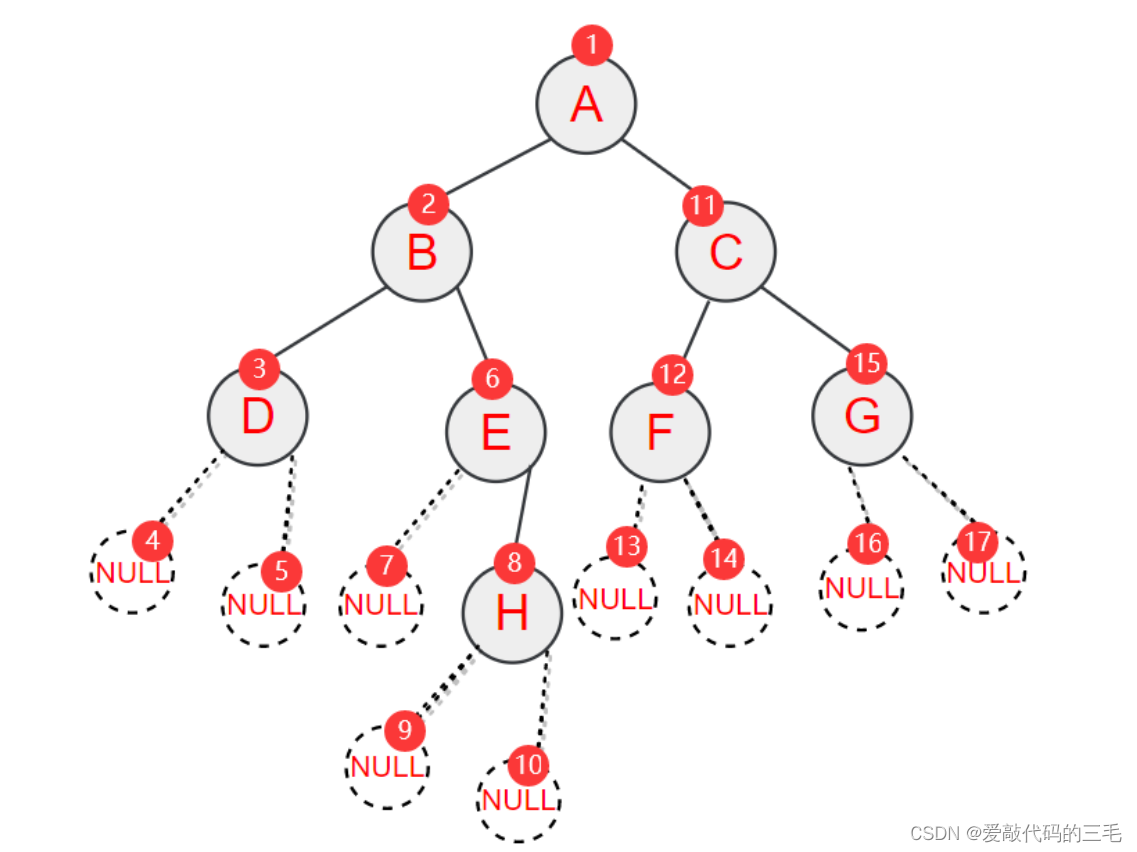
实现思路：

1. 函数三个参数，数组、字符串长度、数组下标，通过递归来构建
2. 递归的结束条件，数组遍历完了、或者是遇到#了
3. 每调用一次函数就让index加一
4. 最后返回节点

// 根据前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* arr, int n, int* index)
{
	if (*index >= n || arr[*index] == '#')
	{
		return NULL;
	}
	BTNode* root = (BTNode*)(malloc(sizeof(BTNode)));
	root->data = arr[*index];
	(*index)++;
	root->left = BinaryTreeCreate(arr, n, index);
	(*index)++;
	root->right = BinaryTreeCreate(arr, n, index);

	return root;
}

层序遍历

层序遍历就是将二叉树按层一层一层遍历。

下面这个二叉树的层序遍历为ABCDEFGH

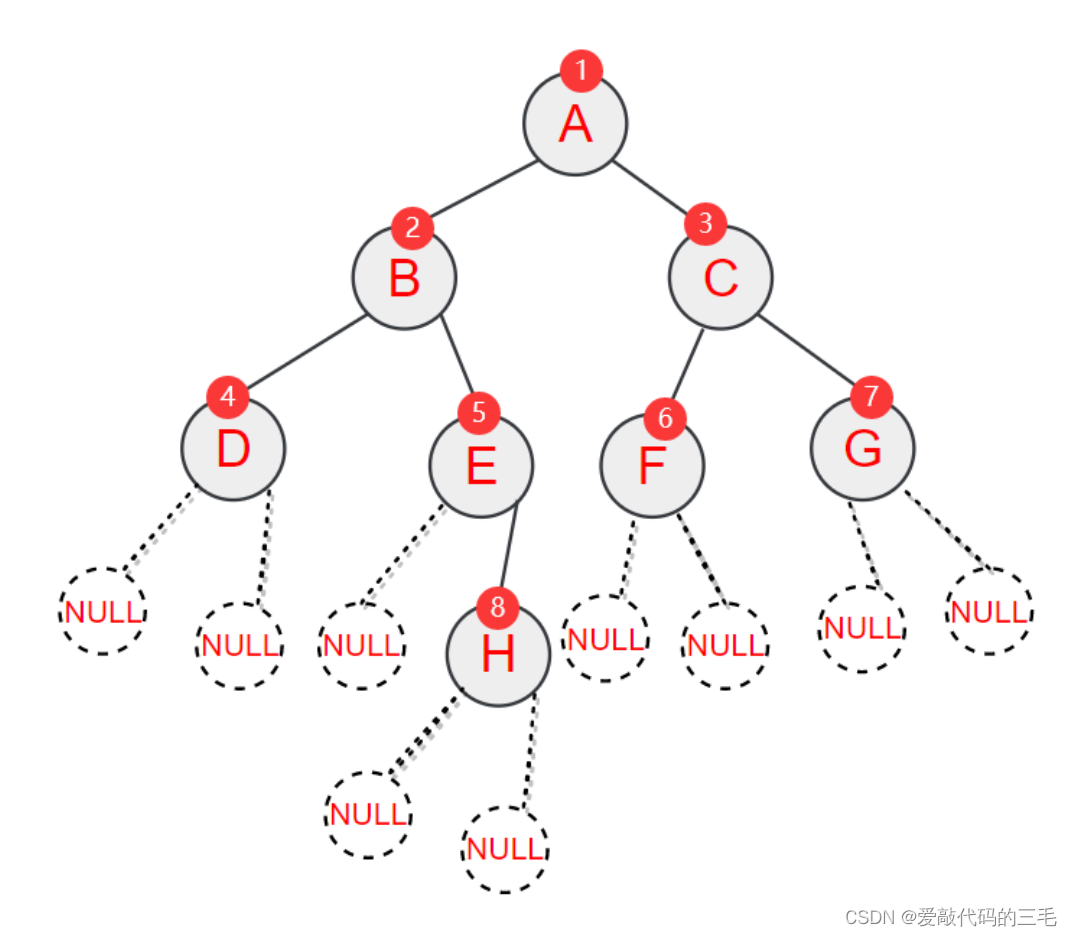
思路：

同过队列来进行广度优先搜索。

• 首先将根节点如队列，然后出队出队的同时将左右孩子入队列(注意左右孩子不为空)
• 出队前记录当前队列元素个数，出当前队列中的元素(避免刚入队的左右子树出队列)
• 当队列为空时说明层序遍历完成

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q = {NULL,NULL};
	QueueInit(&q);
	QueuePush(&q,root);
	while (!QueueEmpty(&q))
	{
		int size = QueueSize(&q);
		while (size--)
		{
			BTNode* root = QueueFront(&q);
			printf("%c ", root->data);
			if (root->left != NULL)
			{
				QueuePush(&q, root->left);
			}
			if (root->right != NULL)
			{
				QueuePush(&q, root->right);
			}
			QueuePop(&q);
		}
	}

}

在二叉树中查找指定值

直接递归遍历二叉树，先找根节点再找左子树和右子树。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}

	BTNode* left = BinaryTreeFind(root->left, x);
	if (left != NULL)
	{
		return left;
	}
	BTNode* right = BinaryTreeFind(root->right, x);
	if (right != NULL)
	{
		return right;
	}
	return NULL;

}

获取二叉树节点个数

这其实就时一个普通的遍历，通过递归将大事化小。整棵树的节点个数会等于：它的左子树节点个数加上右子树的节点个数再加上自己，也就是加一。

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{

	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

获取叶子节点个数

叶子节点右一个特点，就是它的左子树和右子树都为空，通过递归如果左右子树都为NULL就返回1，否则返回0,就能得到叶子节点个数。

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

求二叉树的高度

二叉树的高度就是它的最大深度，相求一颗树的最大深度，就得先求出它的左右子树的最大深度，通过后续遍历到达叶子节点，从叶子节点开始不断求出左右子树的较大的那一棵子树再加一，开始不断向上返回就能得到一颗二叉树的最大深度。

int maxDepth(BTNode* root){
    if (root == NULL)
    {
        return 0;
    }
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);

    return left > right ? left+1 : right+1;

}

从叶子节点开始不断求出左右子树的较大的那一棵子树再加一，开始不断向上返回就能得到一颗二叉树的最大深度。

int maxDepth(BTNode* root){
    if (root == NULL)
    {
        return 0;
    }
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);

    return left > right ? left+1 : right+1;

}

---