LeetCode 647回文子串
题目简析:
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
思路分析:
本题的难点 主要在,思考dp定义以及遍历顺序,分析出几种情况
首先根据题目我们就给出dp定义
//dp[i][j]:区间[i,j]的串是为回文子串,注意是左闭右闭
由dp的定义决定我们使用的数组是boolean类型的
分析有几种情况:
//①首尾指向同一个字符(表示单个字符)
//②首尾中间间隔一个字符,也是回文子串(aba)
//③其余的情况:判断内部是否为回文子串(aabaa)
这个判断内部有点讲究,也决定了遍历顺序,内部,自然是[i+1,j-1],解释一下,即当发现首尾字符相同的时候,说明我们该判断当前区间的串是否为回文子串了
首尾没超过三,举例(单个字符:a,三个字符:aba),可以发现都是回文串
而如果首尾长度超过3,说明我们需要判断内部是否为回文子串
举例(aabaa,aabca)
因此dp[i][j] = dp[i+1][j-1],发现当前位是由它左下角来推出的
//即当前位置的左下角,那么就是从左下角开始往右上角推算dp //一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的
public int countSubstrings(String s) {
int len = s.length();
boolean[][] dp = new boolean[len][len];
int res = 0;
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) {
res++;
dp[i][j] = true;
}
else if (dp[i + 1][j - 1]) {
//表示区间内部:i+1,j-1
res++;
dp[i][j] = true;
}
}
}
}
return res;
}还有一种双指针的方法,就作为了解咯,从中心往外推有几个回文串,有两种情况,中心有一个字符,中心有两个字符
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
//总共有2 * len - 1个中心点
for (int i = 0; i < 2 * len - 1; i++) {
int left = i / 2, right = left + i % 2;
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
//如果当前是一个回文串,则记录数量
ans++;
left--;
right++;
}
}
return ans;
}LeetCode 516最长回文子序列
题目简析;
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
思路分析:
首先要记清楚子序列定义,不改变相对顺序的情况下,不要求连续
按照步骤分析清楚,有了上面一题的启发,这题dp定义,遍历顺序没有那么难想
//dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
//画图看方程,找状态,由上一题的启发,我们判断回文串应该从内部开始判断 //首尾相同的时候,从内部开始判断 //遍历顺序,由dp方程可以看见,当前位由左下角退出,或者左,或者下 //因此得由下往上,由左往右推 //j不从i开始是因为,dp方程决定,两者永远不会指向同一个字符
本题难点倒是dp方程的推导,以及最后的返回结果(由遍历顺序可以决定返回值一定是右上角)
dp的推导也是由上一题的启发,应该从中间往两边推,这里把代码随想录的图拿过来了
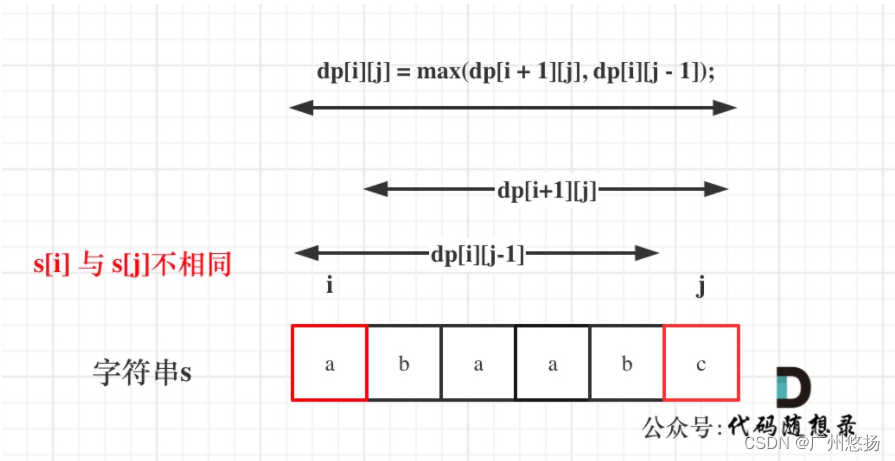
public int longestPalindromeSubseq(String s) {
int len = s.length();
//将区间对应下标会好理解,+1
int [][]dp = new int[len+1][len+1];
//初始化:单个字符,即首尾相同,指向同一单个字符的情况,一定是回文子序列,
// 全初始为1
for (int i = 0; i < len; i++) {//其实就是对角线
dp[i][i] = 1;
}
for (int i = len-1; i >= 0; i--) {
for (int j = i+1; j < len; j++) {
if(s.charAt(i)==s.charAt(j)){
//首尾相等,内部+2
dp[i][j] = dp[i+1][j-1] + 2;
}else{
//首尾不等:找左边或右边最大
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][len - 1];
}