作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:牛客面试必刷TOP101
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!!!
文章目录
前言
一、跳台阶
题目描述
题目解析
二、不同路径的数目(一)
题目描述
题目解析
总结

前言
一、跳台阶
题目描述
描述:
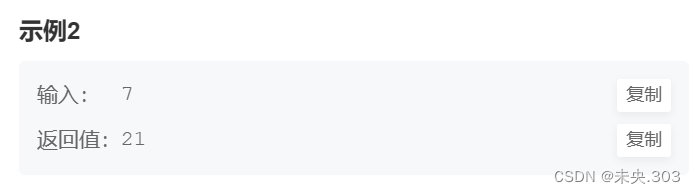
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
数据范围:1≤n≤40
要求:时间复杂度:O(n) ,空间复杂度: O(1)。
示例1:
示例2:
题目解析
解题思路:
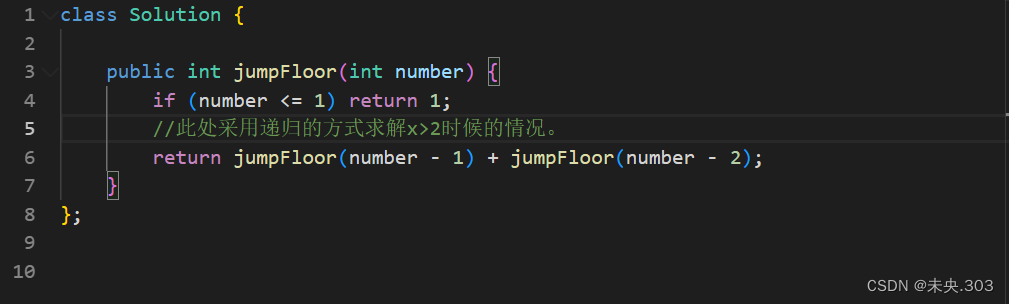
假设f[i]表示在第i个台阶上可能的方法数。逆向思维。如果我从第n个台阶进行下台阶,下一步有2中可能,一种走到第n-1个台阶,一种是走到第n-2个台阶。
所以f[n] = f[n-1] + f[n-2]. 那么初始条件了,f[0] = f[1] = 1。
所以就变成了:f[n] = f[n-1] + f[n-2], 初始值f[0]=1, f[1]=1,目标求f[n] 。
和斐波那契数列的模式一样。
代码解析:
二、不同路径的数目(一)
题目描述
描述:
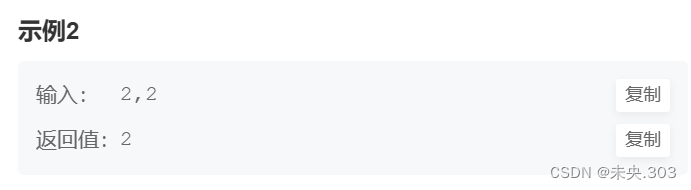
一个机器人在m×n大小的地图的左上角(起点)。
机器人每次可以向下或向右移动。机器人要到达地图的右下角(终点)。
可以有多少种不同的路径从起点走到终点?
备注:m和n小于等于100,并保证计算结果在int范围内;
数据范围:0<n,m≤100,保证计算结果在32位整型范围内
要求:空间复杂度 O(nm),时间复杂度 O(nm)
进阶:空间复杂度 O(1),时间复杂度O(min(n,m))
示例1:
示例2:
题目解析
解题思路:
首先我们在左上角第一个格子的时候,有两种行走方式:如果向右走,相当于后面在一个(n−1)∗m的矩阵中查找从左上角到右下角的不同路径数;而如果向下走,相当于后面在一个n∗(m−1)的矩阵中查找从左上角到右下角不同的路径数。
而(n−1)∗m的矩阵与n∗(m−1)的矩阵都是n∗m矩阵的子问题,因此可以使用递归。
解题步骤:
- step 1:(终止条件) 当矩阵边长n减少到1的时候,很明显只能往下走,没有别的选择了,只有1条路径;同理m减少到1时也是如此。因此此时返回数量为1.
- step 2:(返回值) 对于每一级都将其两个子问题返回的结果相加返回给上一级。
- step 3:(本级任务) 每一级都有向下或者向右两种路径选择,分别进入相应分支的子问题。
代码解析:
总结