统计子岛屿

题目描述

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的 数目 。

思路：

对于(i, j)来说，有四种情况

case1:grid1[i][j] = 1, grid2[i][j] = 1.

case2:grid1[i][j] = 1, grid2[i][j] = 0.

case3: grid1[i][j] = 0, grid2[i][j] = 1.

case4: grid1[i][j] = 0, grid2[i][j] = 0.

对于case4，我们完全不用关心；剩下的case1、case2、case3我们再看，由于是grid1包含grid2，对于case3，如果grid2是陆地，grid1是海水，那么grid1就不包含grid2，那么我们就可以提前干掉grid2中的点；对于case2，如果grid1是陆地，grid2是海水，那么grid2必然不是grid1的子岛，我们可以不做任何操作；对于case1，那么grid2必然是grid1的子岛，我们就计数，然后dfs。

下面看代码：

	public int countSubIslands(int[][] grid1, int[][] grid2) {
        int m = grid1.length, n = grid1[0].length, count = 0;
        // 先排除不是子岛屿的节点
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(grid2[i][j] == 1 && grid1[i][j] == 0){
                    dfs(grid2, i, j, m, n);
                }
            }
        }
        System.out.println("======");
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
            	// 对于条件case1和case2来说
            	// 这块可以优化成if(grid2[i][j] == 1)
                if(grid2[i][j] == 1 && grid1[i][j] == 1){
                    count++;
                    dfs(grid2, i, j, m, n);
                }
            }
        }
        return count;
    }

    public void dfs(int[][] grid, int i, int j, int m, int n){
        if(i >= m || i < 0 || j >= n || j < 0
                || grid[i][j] == 0 ){
            return;
        }
        grid[i][j] = 0;
        dfs(grid, i + 1, j, m, n);
        dfs(grid, i - 1, j, m, n);
        dfs(grid, i, j + 1, m, n);
        dfs(grid, i, j - 1, m, n);
    }

    public static void main(String[] args) {
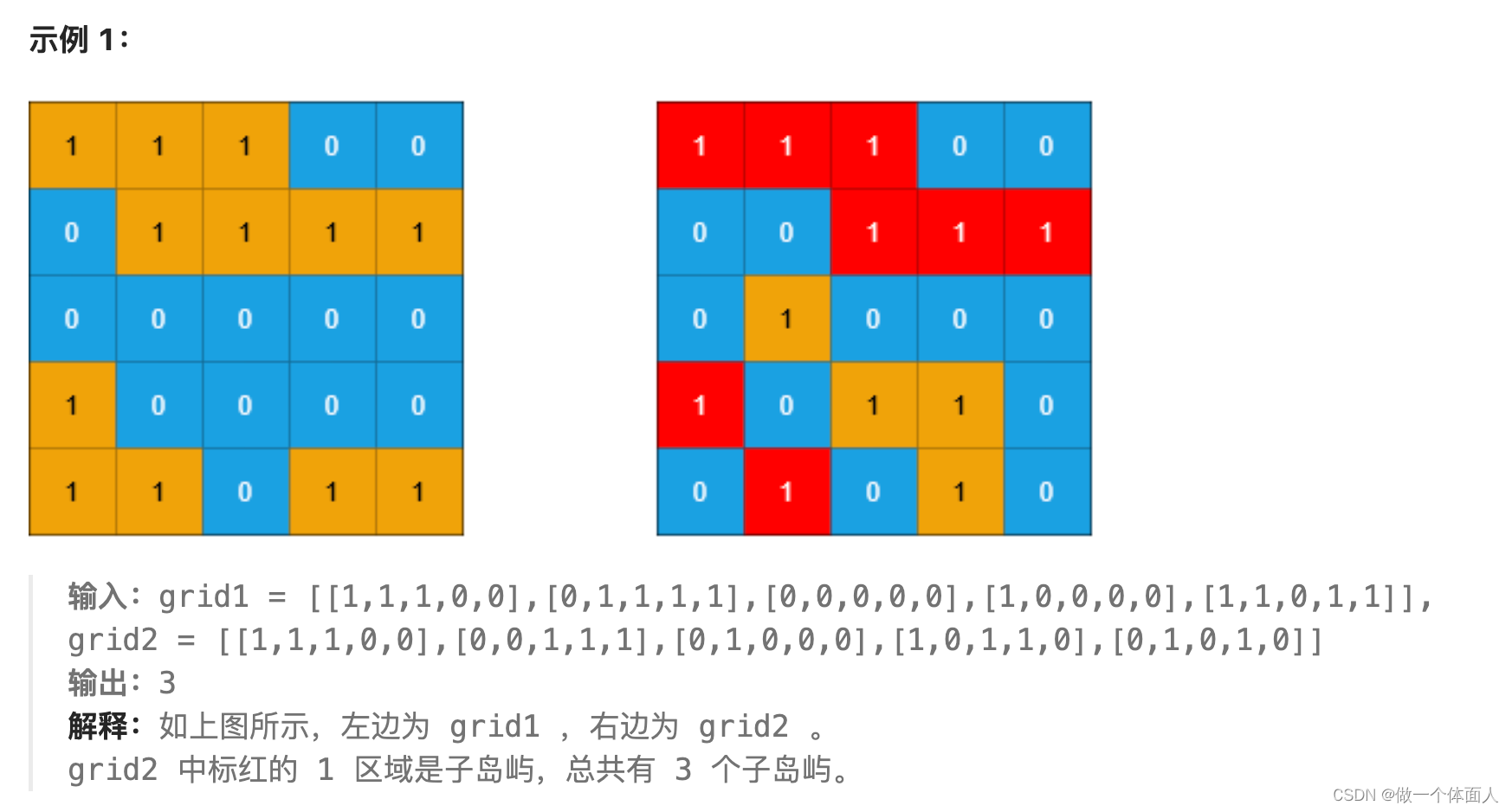
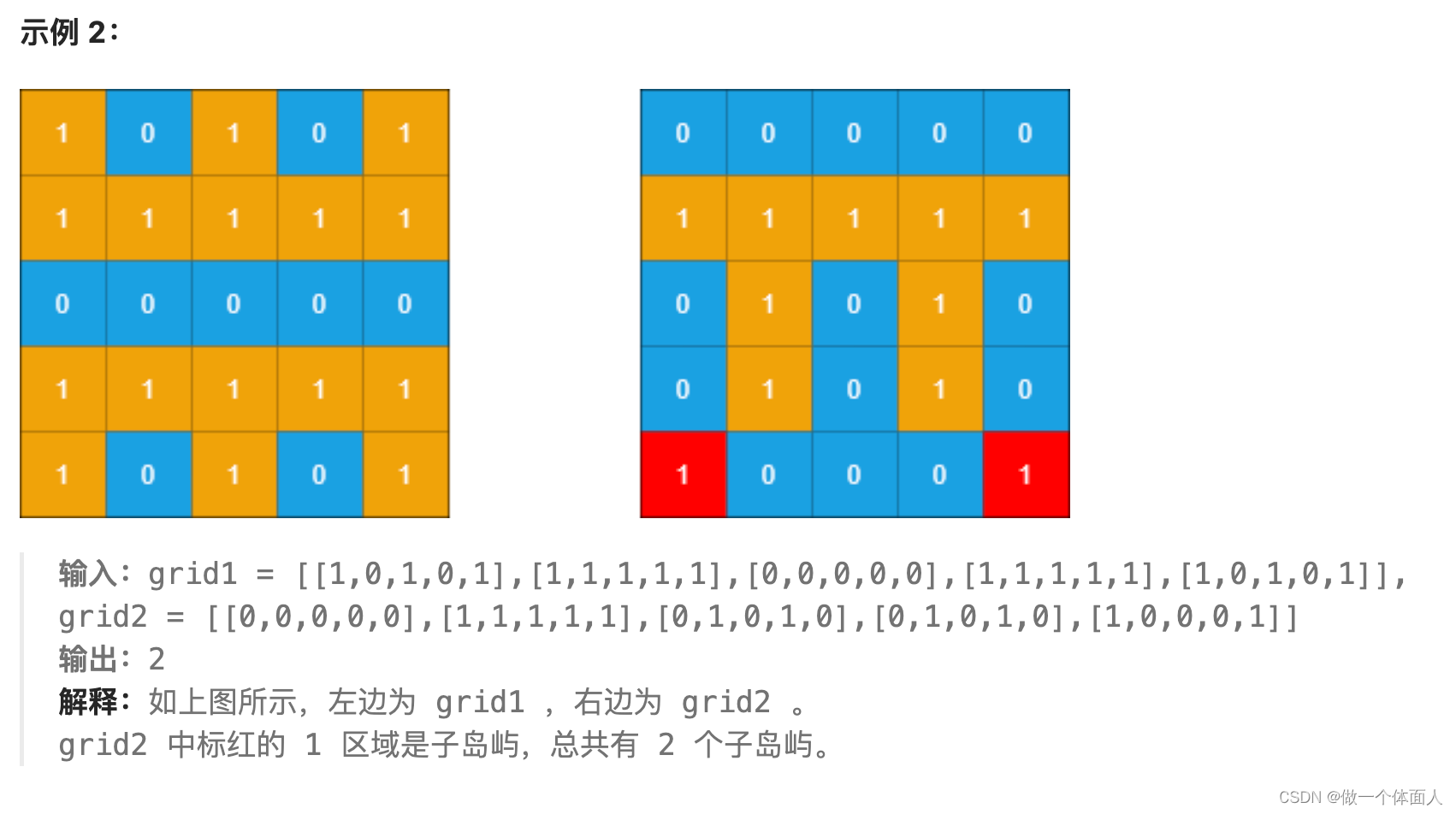
        int[][] grid1 = {{1,1,1,0,0},{0,1,1,1,1},{0,0,0,0,0},{1,0,0,0,0},{1,1,0,1,1}};
        int[][] grid2 = {{1,1,1,0,0},{0,0,1,1,1},{0,1,0,0,0},{1,0,1,1,0},{0,1,0,1,0}};
        CountSubIslands countSubIslands = new CountSubIslands();
        countSubIslands.countSubIslands(grid1, grid2);

    }