题目链接

Leetcode.2867 统计树中的合法路径数目 rating : 2428

题目描述

给你一棵 $n$ 个节点的无向树，节点编号为 $1$ 到 $n$ 。给你一个整数 $n$ 和一个长度为 $n-1$ 的二维整数数组 $edges$ ，其中 $edges[i]=[u_i,v_i]$ 表示节点 $u_i$ 和 $v_i$ 在树中有一条边。

请你返回树中的 合法路径数目 。

如果在节点 $a$ 到节点 $b$ 之间 恰好有一个 节点的编号是质数，那么我们称路径 $(a,b)$ 是 合法的 。

注意：

• 路径 $(a,b)$ 指的是一条从节点 $a$ 开始到节点 $b$ 结束的一个节点序列，序列中的节点 互不相同 ，且相邻节点之间在树上有一条边。
• 路径 $(a,b)$ 和路径 $(b,a)$ 视为 同一条 路径，且只计入答案 一次 。

示例 1：

输入：n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
输出：4
解释：恰好有一个质数编号的节点路径有：

• (1, 2) 因为路径 1 到 2 只包含一个质数 2 。
• (1, 3) 因为路径 1 到 3 只包含一个质数 3 。
• (1, 4) 因为路径 1 到 4 只包含一个质数 2 。
• (2, 4) 因为路径 2 到 4 只包含一个质数 2 。
  只有 4 条合法路径。

示例 2：

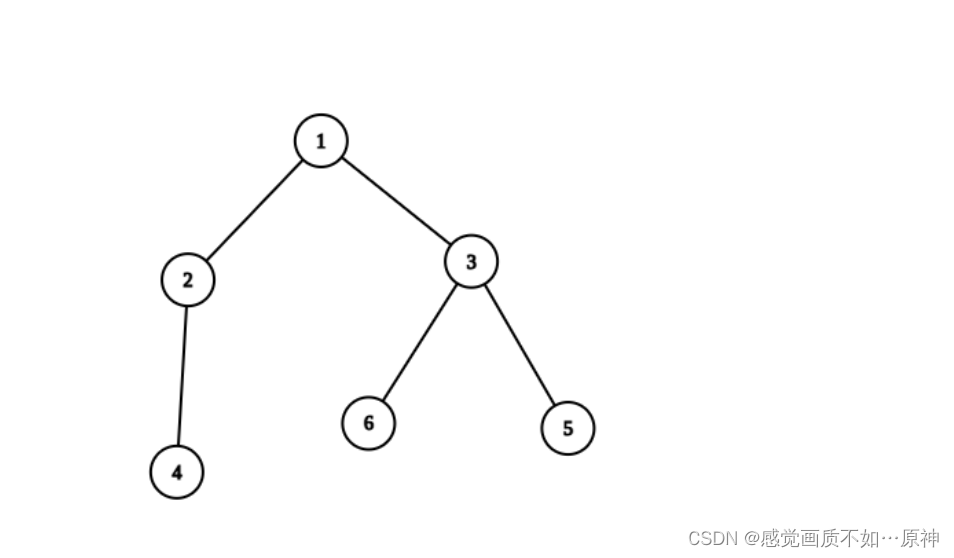
输入：n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
输出：6
解释：恰好有一个质数编号的节点路径有：

• (1, 2) 因为路径 1 到 2 只包含一个质数 2 。
• (1, 3) 因为路径 1 到 3 只包含一个质数 3 。
• (1, 4) 因为路径 1 到 4 只包含一个质数 2 。
• (1, 6) 因为路径 1 到 6 只包含一个质数 3 。
• (2, 4) 因为路径 2 到 4 只包含一个质数 2 。
• (3, 6) 因为路径 3 到 6 只包含一个质数 3 。
  只有 6 条合法路径。

提示:

• $1\le n\le 10^5$
• $edges.length=n-1$
• $edges[i].length=2$
• $1\le u_i,v_i\le n$
• 输入保证 $edges$ 形成一棵合法的树。

解法：筛质数 + dfs

我们先将 $[1,10^5]$ 内的质数筛出来，用 $np$ 记录。如果 $np[x]=true$，说明 $x$ 不是质数；否则是质数。

我们可以从 质数点 $x$ 出发，开始 dfs，访问非质数点，因为一条 合法路径 只存在一个质数点。

通过上述操作，可以将 $x$ 连接的几个 非质数连通块 计算出来。

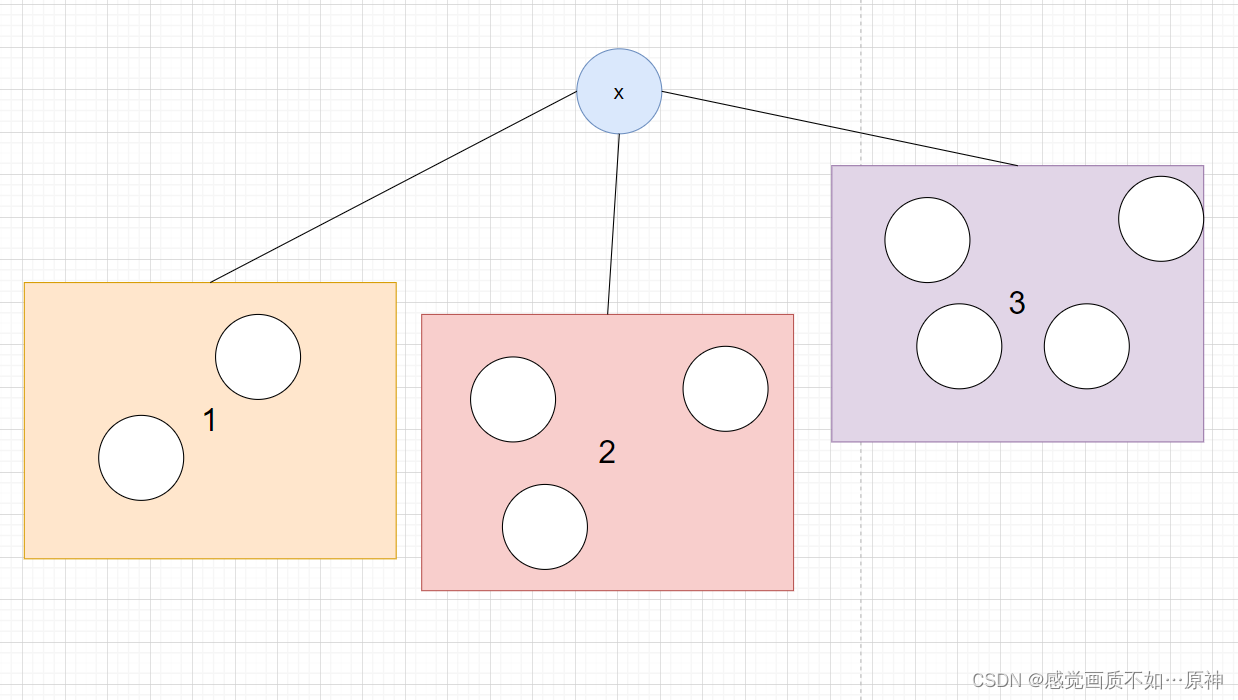
假设如上图，通过 $x$ 分割出了三个 非质数连通块 ，每个连通块中的节点数量分别为 $2,3,4$。

我们现在来计算 合法路径数量（从左到右计算，保证不重不漏）：

• $1$号连通块 通过 $x$ 和 $2$号联通块 组成的路径数为 $2\times 3=6$；
• $1$号连通块,$2$号连通块 通过 $x$ 和 $3$号连通块 组成的路径数为 $(2+3)\times 4=20$；
• 以及所有连通块的节点数量 $9$

上图通过 $x$ 的合法路径条数为 $6+20+9=35$。

我们可以用一个数组 $sz$，记录下已经计算过的连通块数量。假设 $1$ 号连通块中的两个节点分别为 $i,j$，那么 $sz[i]=sz[j]=2$。

如果下一次有另外一个 质数点 $y$ 和这个 $1$号连通块 相连，那么我们就可以直接计算，不用再次遍历记录连通块节点的数量。

时间复杂度：$O(n)$

C++代码：

using LL = long long;

const int MX = 1e5;
bool np[MX + 1];

auto init = []() ->int{
    np[1] = true;
    for(int i = 2;i * i <= MX;i++){
        if(!np[i]){
            for(int j = i * i;j <= MX;j += i) np[j] = true;
        }
    }
    return 0;
}();

class Solution {
public:
    long long countPaths(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n + 1);
        for(auto &e:edges){
            auto a = e[0] , b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }

        vector<int> sz(n + 1);
        vector<int> nodes;

        function<void(int,int)> dfs = [&](int x,int fa) ->void{
            nodes.push_back(x);
            for(auto y:g[x]){
                if(y == fa || !np[y]) continue;
                dfs(y,x);
            }
        };

        LL ans = 0;
        for(int x = 1;x <= n;x++){
            if(np[x]) continue; //合数就跳过 ， 是以质数为起点dfs

            LL sum = 0;
            for(auto y : g[x]){
                //接着要求的是合数的连通块
                if(!np[y]) continue;

                //如果这个连通块没有被计算过，就计算
                if(sz[y] == 0){
                    nodes.clear();
                    dfs(y,-1);
                    for(auto node:nodes) sz[node] = nodes.size();
                }

                ans += sum * sz[y];
                sum += sz[y];
            }

            ans += sum;
        }

        return ans;
    }
};