风玫瑰图的作用

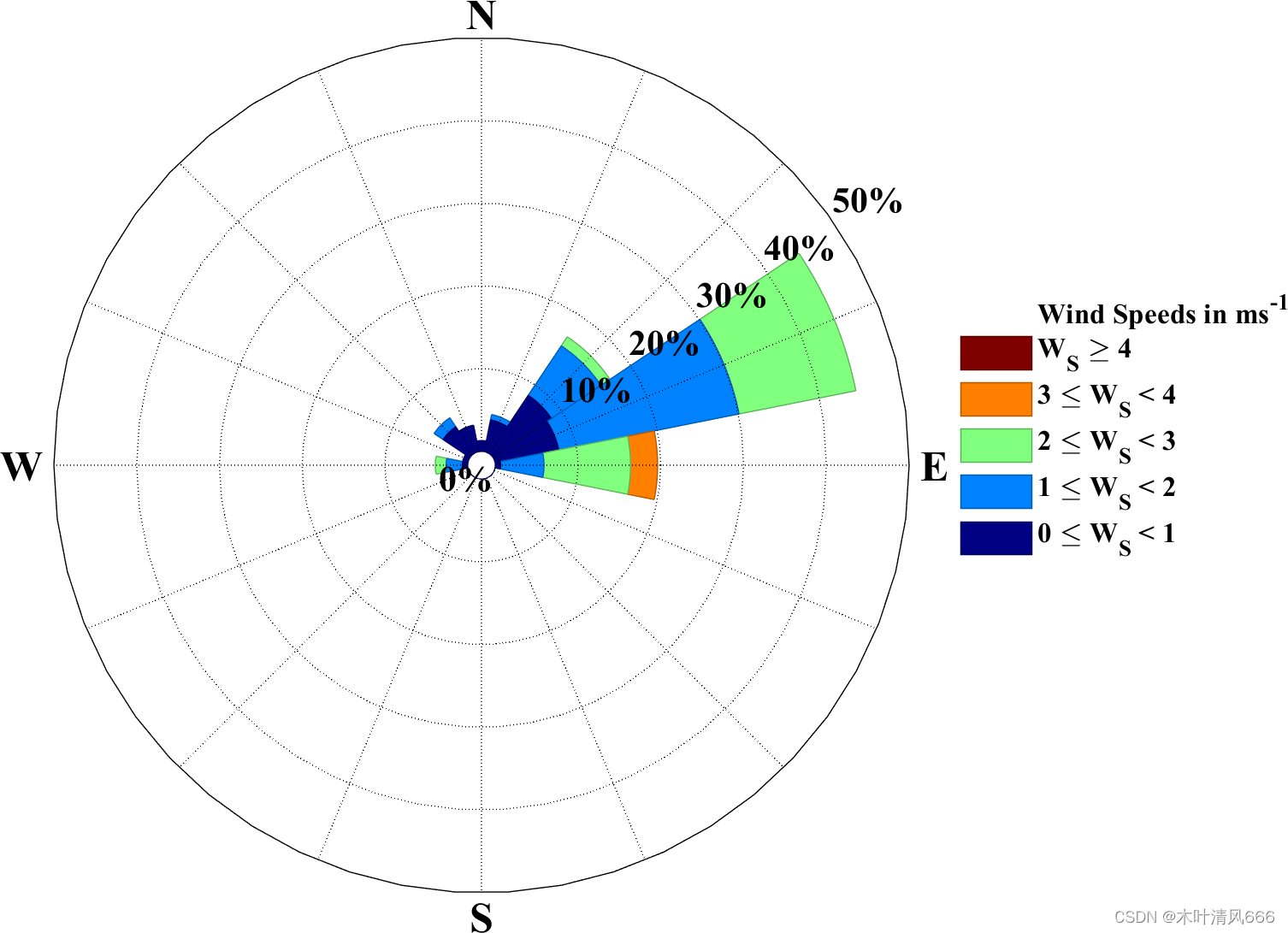
• 风玫瑰图（Wind Rose Plot）是一种用于可视化风向和风速分布的图表。它通常以极坐标形式呈现，其中角度表示风向，半径表示风速的频率或相对概率。风玫瑰图对于理解和呈现气象数据、海洋学研究以及其他需要分析和可视化风向风速信息的领域非常有用。以下是一些绘制风玫瑰图的作用：

  • 风向和风速分布分析： 风玫瑰图可以清晰地显示特定地区或时间段内的风向和风速分布情况。这对于气象学家、气象学研究者以及气象数据分析人员来说是有用的。

  • 风能评估： 在可再生能源领域，特别是风能行业中，风玫瑰图用于评估风场的分布情况。这有助于确定最适合建造风力发电厂的地点。

  • 航海和航空： 在航海和航空领域，了解风向和风速对于船只和飞机的航行和导航非常重要。风玫瑰图提供了一种直观的方式来查看这些信息。

  • 气象教育： 风玫瑰图可以用于教育目的，帮助学生理解气象学中的风向和风速概念。它们为学习者提供了一个直观的视觉工具，使他们能够更好地理解风的变化和分布。

  • 气候研究： 风玫瑰图在研究气候和气象条件方面提供了有益的信息，特别是在分析长期气象数据时。

  • 环境规划： 对于一些需要考虑风向和风速的环境规划项目，例如城市规划、建筑设计等，风玫瑰图可以提供决策支持。

Matlab代码实现

%% Figrue4-13 逐日风玫瑰图
clear;clc;close all
load('.\data\BFT_wind2_daily_7920.mat')

x_0=0.1;
y_0=0.20;
len=0.60;
width=0.60;
d_x=0.43;
d_y=-0.30;
px=[0 0 0 1];
py=[0 1 1 1];
siz=25;lind=1.5;ms=18;

uc=nanmean(u,2);
vc=nanmean(v,2);
speed=sqrt(vc.^2+uc.^2);
tangle=atand(uc./vc)+360;
set(gcf,'color',[1 1 1],'position',[10 45 800 800*1.2]);%get(0,'screensize')
axes('position',[x_0+d_x*px(1), y_0+d_y*py(1), len, width]);

WindRose(tangle(121:273),speed(121:273),'ndirections',16,'speedround',...
       [1],'freqlabelangle',[35],'nspeeds',[5],'maxfrequency',[50]);
title('')
set(get(gca,'legend'),'position',[0.7313 0.4401 0.2412 0.1672]);

% export_fig(['.\map\','Figure4-13风玫瑰图.png'],'-r200')
% close all

结果展示