二叉树中的常用方法
静态二叉树的手动创建
这里我们先给出二叉树结点的信息(这里是内部类):
static class TreeNode {
public char val;
public TreeNode left;//左孩子的引用
public TreeNode right;//右孩子的引用
public TreeNode(char val) {
this.val = val;
}
}手动创建的代码如下:
/**
* 创建一棵二叉树 创建成功后 返回根节点
* @return
*/
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
return A;
}利用new出结点对象和左右指针的连接,我们就可以创建一棵这样的简单二叉树。(给你们画了个图嘿嘿)。
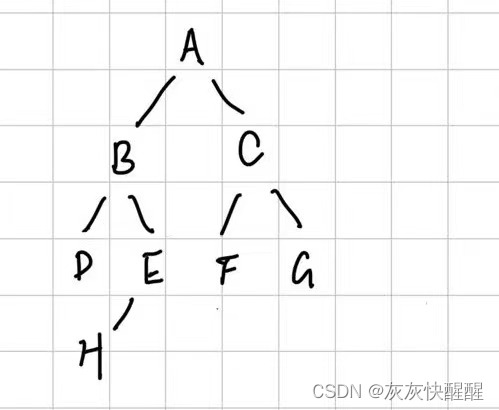
获取树中结点的个数
这里依然是用到了树的递归的思想:我们可以使用递归左树右树的方法,利用一个常量来记录结点的个数。
public static int nodeSize;
/**
* 获取树中节点的个数:遍历思路
*/
void size(TreeNode root) {
if(root == null) {
return;
}
nodeSize++;
size(root.left);
size(root.right);
}但是更推荐用子问题的思想,即:一棵树的结点个数 = 左树的结点个数 + 右数的节点个数+ 根结点(即1),像这种利用递归方法的返回值计算我们就称为子问题思路。代码如下:
/**
* 获取节点的个数:子问题的思路
*
* @param root
* @return
*/
int size2(TreeNode root) {
if(root == null) {
return 0;
}
return size2(root.left) + size2(root.right) + 1;
}获取叶子结点的个数
求叶子结点,在代码上,就是求含有多少左边和右边都是null的节点数(如果一个节点满足这样的条件就++),像上面一样,先给出遍历的方法:
/*
获取叶子节点的个数:遍历思路
*/
public static int leafSize = 0;
void getLeafNodeCount1(TreeNode root) {
if(root == null) {
return;
}
if(root.right == null && root.left == null) {
leafSize++;
}
getLeafNodeCount1(root.left);
getLeafNodeCount1(root.right);
}下面是子问题的思路:
/*
获取叶子节点的个数:子问题
*/
int getLeafNodeCount2(TreeNode root) {
if(root == null) {
return 0;
}
int leftCount = getLeafNodeCount2(root.left);
int rightCount = getLeafNodeCount2(root.right);
//满足条件:即左右返回值+1, 不满足条件:还是给出原来的左右返回值
return root.right == null && root.right == null ? leftCount + rightCount + 1 : leftCount + rightCount;
}
获取一棵树第k层的节点数目
还是主要利用递归的思想:一棵树第k层的结点数 = 左树第k-1层的节点数 + 右树第k-1层的节点数。递归的截止条件就是:当k为1时,直接返回1即可,如果为空则返回0。那么所以,代码如下:
/*
获取第K层节点的个数
*/
int getKLevelNodeCount(TreeNode root, int k) {
if(root == null) {
return 0;
}
if(k == 1) {
return 1;
}
//获取左树第k-1层的节点数
int leftCount = getKLevelNodeCount(root.left, k - 1);
//获取右树第k-1层的节点数
int rightCount = getKLevelNodeCount(root.right, k - 1);
//返回左右树之和
return leftCount + rightCount;
}获取二叉树的深度
还是利用递归的思想(截止条件:为空返回零):一棵二叉树的深度 = 左树和右树之中最高的那一个的深度 + 1.
利用我们之前学的子问题思想和递归,可以轻松写出:
int getHeight(TreeNode root) {
if(root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
//返回深度最大的那一个的深度 + 1
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}检查树中是否有值为value的结点(即返回该节点)
还是利用之前的递归思路:value可能在当前结点,也可能在左右树当中,亦有可能不存在。
这里一定要注意一个点:如果已经提前找到了目标节点,就直接返回即可(比如在左树当中找到了,就不用在右树当中找了),这样做可以大大节约时间。
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val) {
if(root == null) {
return null;
}
if(root.val == val) {
return root;
}
TreeNode ret1 = find(root.left, val);
//不再去右边了
if(ret1 != null) {
return ret1;
}
TreeNode ret2 = find(root.right, val);
if(ret2 != null) {
return ret2;
}
return null;
}层序遍历
层序遍历,在上一篇中我也有讲,就是对一棵树进行从上到下,从左到右的遍历操作。那么如何通过代码来实现这一个过程呢?这时我们就可以用到之前的一个数据结构,也就是队列,那么我们如何利用队列来进行层序遍历呢,我们来看下面:
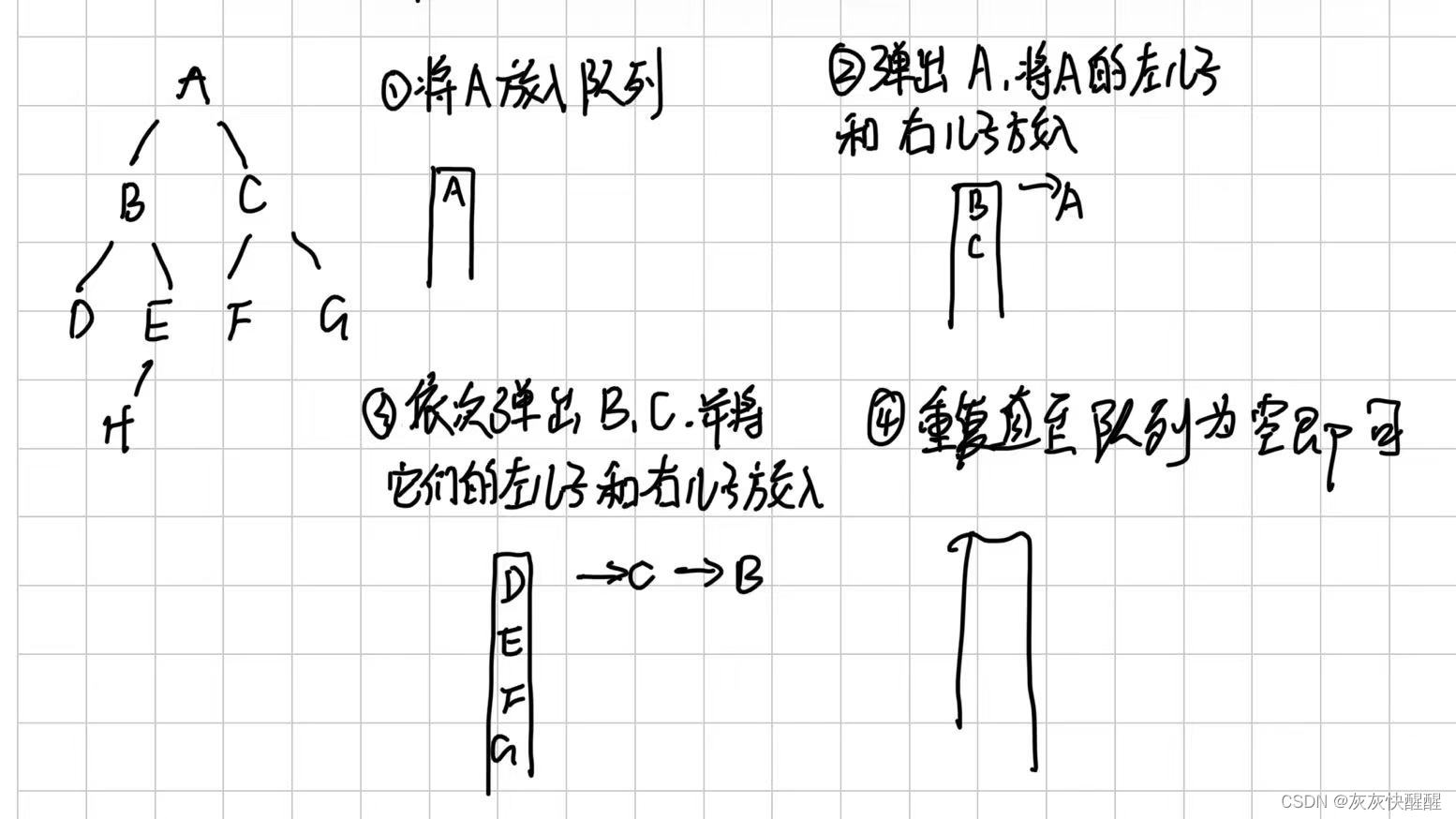
这里注意一个点,当且仅当左/右儿子不为空时,才能批准放入队列,否则跳过。代码如下:
//层序遍历(利用队列)
void levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
//当队列不为空时持续该过程
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if(cur.left != null) {
queue.offer(cur.left);
}
if(cur.right != null) {
queue.offer(cur.right);
}
}
}判断一棵树是否为完全二叉树
我们来回顾一下完全二叉树的性质:即完全二叉树是一棵从上到下,从左到右依次排列元素的树(即直到最后一个结点之后,其余前面的结点都不能为空)。所以我们就浮现出了这样的思路,即还是利用队列来遍历树每次,都将左右儿子放入队列(不论是不是空),当遇到了第一个为空的元素后,立刻停止放入,检查队列中剩余的元素是否有非空的,如果全是null,则是完全二叉树,如果有一个不是,就不是完全二叉树,画图如下:
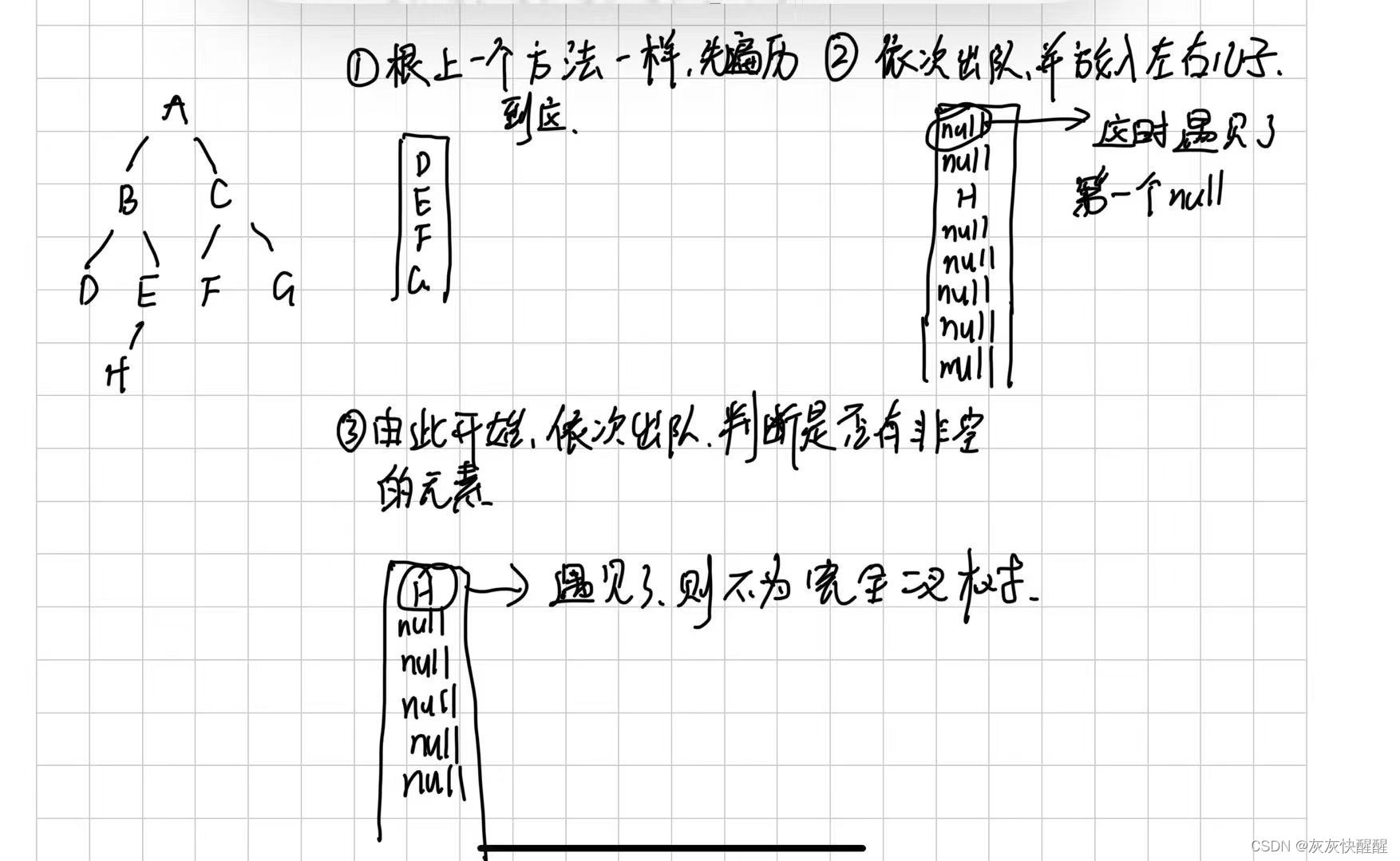
代码如下:
// 判断一棵树是不是完全二叉树
boolean isCompleteTree(TreeNode root) {
if(root == null) {
return true;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
while(cur == null && !queue.isEmpty()) {
TreeNode t = queue.poll();
if(t != null) {
return false;
}
}
queue.offer(cur.left);
queue.offer(cur.right);
}
return true;
}