前言
本系列文章【
数据结构】默认会使用 C/C++ 进行设计实现!其他语言的实现方式请参照分析设计思路自行实现!
注[1]:文章属于学习总结,相对于课本教材而言,不具有相应顺序性!(可在合集中自行查看是否存在相应文章)!
注[2]:如有问题或想让博主进行思路分析的内容,可在后台私信!
文章目录
- 前言
- 完全二叉树的认识
- 堆的基本认识
- 堆的性质 及 大小根堆【重要】
- 堆的结构及其顺序结构(特点)
- 堆的结构认识
- 顺序存储结构
- 向上调整算法
- 算法基本思路(以小根堆为例):
- C/C++ 语言代码设计
- 向下调整算法
- 算法基本思路(以大根堆为例):
- C/C++ 语言代码设计
完全二叉树的认识
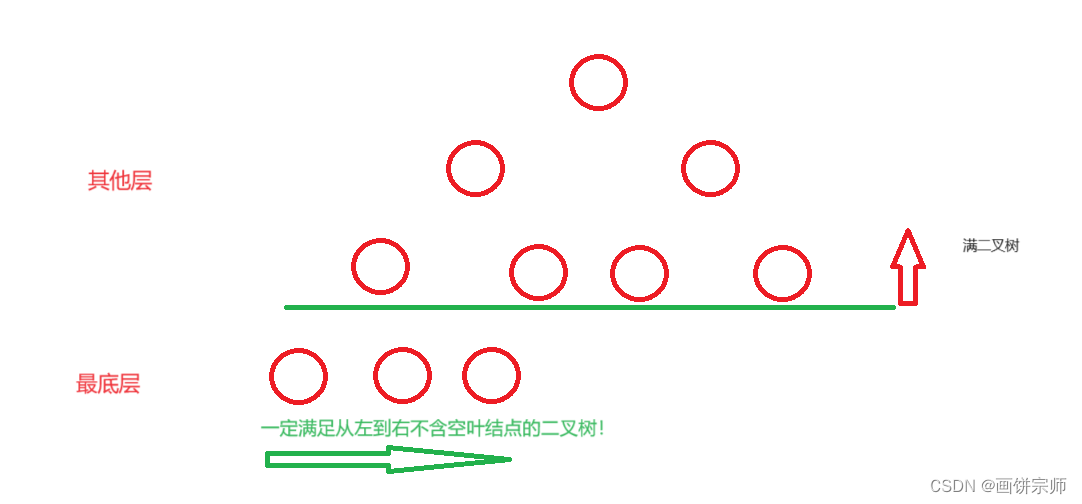
- 完全二叉树的定义:对一颗具有n个结点的二叉树按层序编号,如果编号为 i ( 1 <= i <= n)与同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同,则这颗二叉树称为:完全二叉树。
- 完全二叉树的简单认识(白话描述特点):除了最底层,其他层都是满节点(构成一个满二叉树),最底层一定满足从左到右不含空叶结点的二叉树!
堆的基本认识
- 堆(Heap)是计算机科学中一类特殊的数据结构,是最高效的优先级队列。
- 堆通常是一个可以被看作一棵
完全二叉树的数组对象。

上述图片中的第二行式子,描述的就是:
堆的特性:堆中某个结点的值总是不大于或不小于其父结点的值!
堆的性质 及 大小根堆【重要】
-
堆中某个结点的值总是不大于或不小于其父结点的值! -
堆总是一棵完全二叉树! -
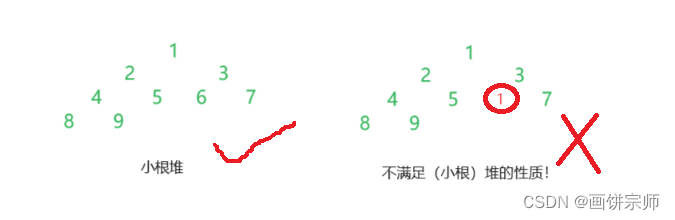
大根堆:即根节点的值最大! -
小根堆:即根节点的值最小!
堆的结构及其顺序结构(特点)
堆的结构认识
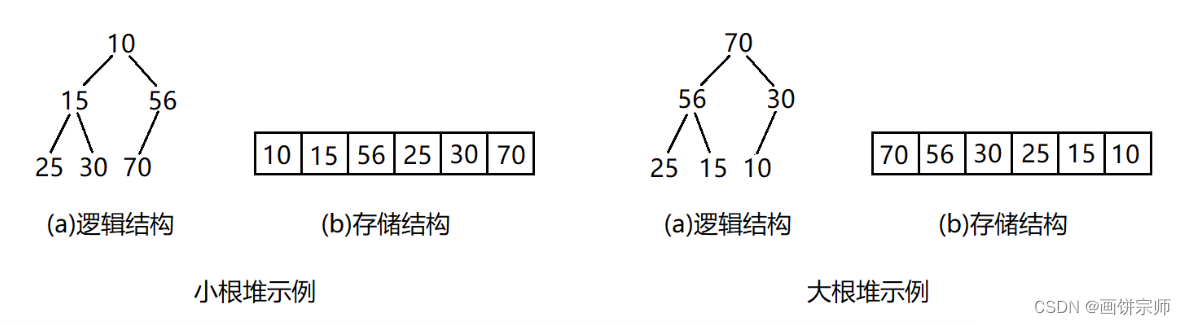
- 在逻辑上,堆的性质之一,堆一定是一个完全二叉树!
- 在存储结构上,由于完全二叉树的层序”排列特点“,我们一般都是使用数组或其他顺序存储结构来作为存储对象,来模拟堆!
顺序存储结构
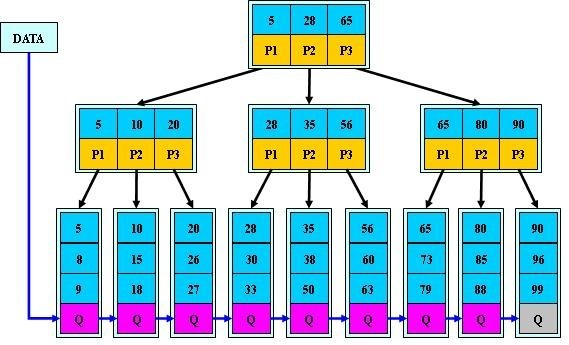
由完全二叉数的图示结构,不难看出,如果按照层序遍历,将其排列成一行,可以形成一个不含空结点(数值)的数组结构!
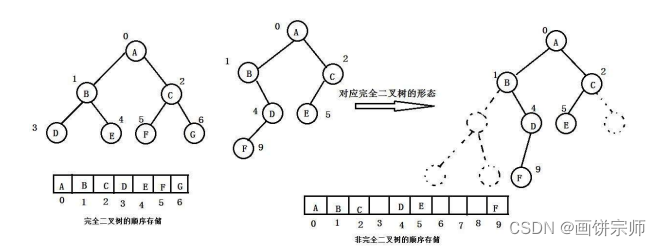
如上图所示,将根节点存储在索引值为:0 的位置!(有如下特点!)
若索引为 i 的结点存在左右子结点,则:
左子树结点索引:2 * i + 1右子树结点索引:2 * i + 2
若已知:左 / 右子结点的索引值为:n,则:
父节点索引为:(n-1) / 2
向上调整算法
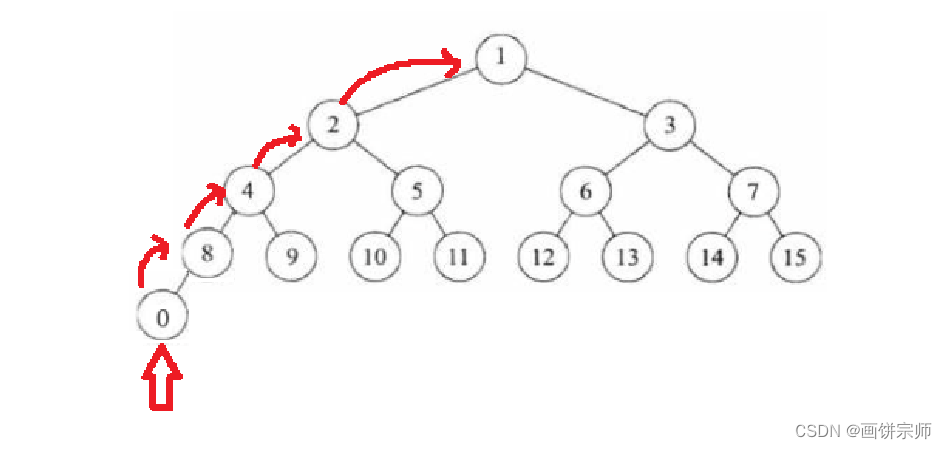
算法基本思路(以小根堆为例):
- 找到不符合堆性质的结点!记为:目标节点!如上图中的:0。
- 将
目标结点与其父节点进行值对比!
- 若目标结点值
小于父节点的值,则进行父子交换! - 若目标结点的值比其父结点的值大,则停止向上调整,此时该树已经是小堆了。
如上图,流程说明:
- 第一次,0 < 8,交换 0 与 8,此时有原来 8 位置上的就是原来的目标值!
- 第二次,0 < 4,交换 0 与 4,
…
如上图中,目标值 0 一定是向上调整到整棵树的根节点位置!
交换中的索引值确认方式:
- 若已知:左 / 右子结点的索引值为:n,则:
- 父节点索引为:(n-1) / 2
C/C++ 语言代码设计
- 由于 C 语言中没有容器,故我们需要动态申请一块内存作为数组存储我们的数据元素(动态内存申请部分将在后文实现)。
- C++ 可以直接使用 vector 来作为容器存储数据。
void Swap(DataType* x, DataType* y)
{
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
/* 向上调整算法 */
// void AdjustUp(vector<DataType>& vec, int idx) // C++
void AdjustUp(DataType* vec, int idx)
{
int parent = (idx-1) / 2; // 记录当前结点的父节点位置!
while(idx > 0){
// 循环条件:目标节点的位置必须合法!
// 注:当目标节点索引为 1 或 2 时,若发生交换则一定会被调整到 0 处!
// 小根堆为例:特点:父小于子!
if( vec[idx] < vec[parent] ){
Swap(&vec[idx], &vec[parent]); // 值交换
idx = parent; // 更新目标值的索引!
parent = (idx-1) / 2; // 更新父节点的索引!
}else break;
}
}
向下调整算法
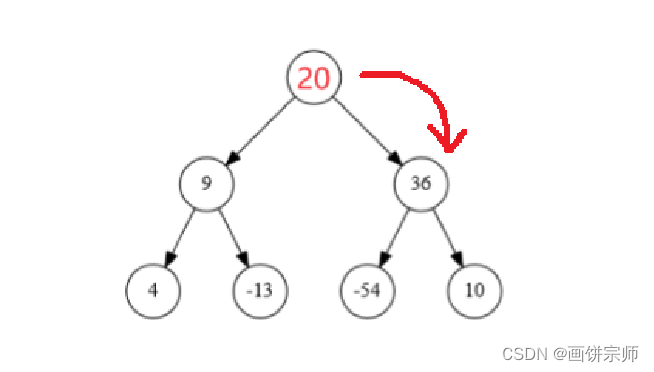
算法基本思路(以大根堆为例):
向下调整算法需要满足一个前提:
若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
- 找到不符合堆性质的结点!记为:目标节点!如上图中的:20。
- 将
目标结点与其较大子节点进行值对比!(大根堆);将目标结点与其较小子节点进行值对比!(小根堆)。 - 以大根堆为例,若目标结点值(父)
小于较大子节点的值,则进行父子交换!
使用堆的向下调整算法,最坏的情况下(即一直需要交换结点),需要循环的次数为:h - 1次(h为树的高度)。而 h = log2(N+1)(N为树的总结点数)。所以
堆的向下调整算法的时间复杂度为:O(logN) 。
如上图,流程说明:
- 第一次,9 < 36,较大值为:36!20 < 36,交换 20 与 36,此时有原来 36 位置上的就是原来的目标值!
- 第二次,-54 < 10,较大值为:10!20 > 10,调整结束!
交换中的索引值确认方式:
- 若已知:父结点的索引值为:n,则:
- 左子树结点索引:2 * n + 1
- 右子树结点索引:2 * n + 2
C/C++ 语言代码设计
void Swap(DataType* x, DataType* y)
{
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
/* 向下调整算法:大根堆 */
// void AdjustUp(vector<DataType>& vec, int idx) // C++
// 参数:size:数组的大小
void AdjustDown(DataType* vec,int size, int idx){
int child = idx*2+1; // child 表示子树索引!
// 此处假设较大值为:左子节点
while( child < size ){
// 判断 左右子结点的大小关系
// 大根堆:选较大的
// 小根堆:选较小的
if( child+1 < size && vec[child+1] > vec[child] ) child++;
if( vec[idx] < vec[child]){
//将父结点与较大的子结点交换
Swap(&vec[child], &vec[idx]);
//继续向下进行调整
idx= child;
child = 2 * idx+ 1;
}else break;
}
}
待更新!