1.介绍
B树是一种自平衡的搜索树数据结构,常用于数据库和文件系统中的索引结构。它具有以下好处和功能:
-
高效的查找操作:B树的特点是每个节点可以存储多个关键字,并且保持有序。通过在节点上进行二分查找,可以快速定位目标关键字的位置,从而实现高效的查找操作。
-
平衡性:B树通过自平衡的方式维护树的平衡性,即保证树的每个叶子节点到根节点的路径长度相等。这种平衡性能够确保各种操作的时间复杂度保持在较低水平,例如插入、删除和查找等操作都可以在对数时间内完成。
-
适应大型数据集:B树适用于存储大型数据集,并且可以处理非常大的索引。其节点可以存储多个关键字,因此在相同层数的情况下,B树可以存储更多的数据。
-
支持范围查询:由于B树的节点有序,因此可以很方便地进行范围查询。通过定位范围的起始和结束关键字所在的节点,可以快速地获取指定范围内的数据。
-
高效的插入和删除操作:B树通过平衡性的维护,使得插入和删除操作具有较低的时间复杂度。它可以通过调整节点的结构,避免过深或过浅的树结构,从而保持树的平衡。
总的来说,B树是一种高效的数据结构,能够应对大规模数据集的索引需求,并提供快速的查找、插入和删除操作。它在数据库和文件系统中广泛应用,为数据的组织和访问提供了便利。
2.代码分析
1.分裂
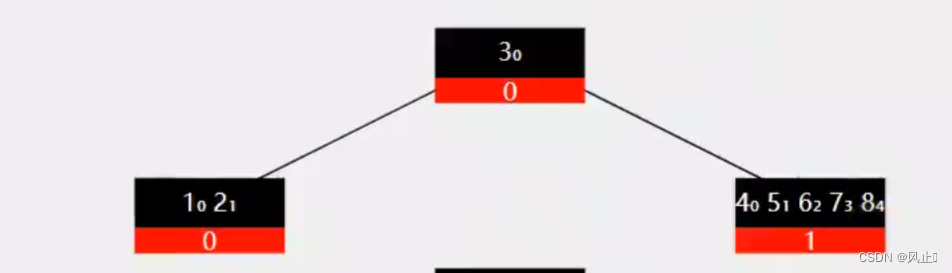
当键的数量超过 2t - 1的时候就会进行分裂操作,规则就是中间的向上分裂,大的交给一个新的节点,小的交给自己
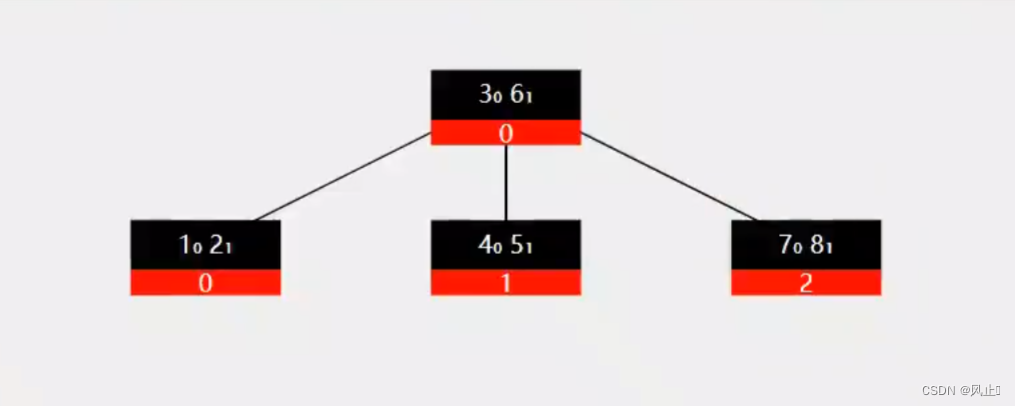
如果不是叶子节点就需要把后半部分子节点给新的节点,
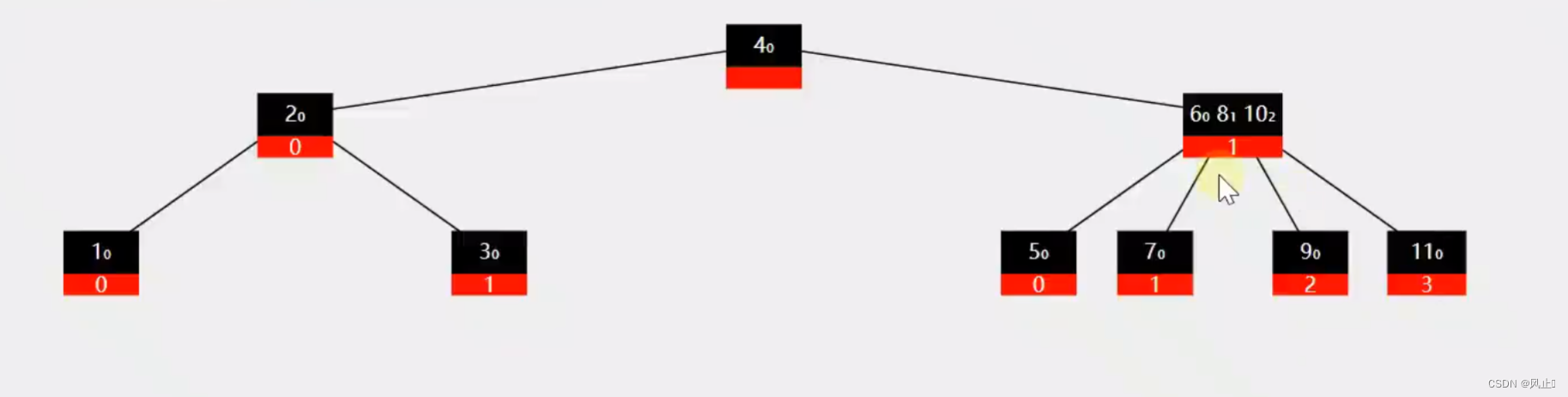
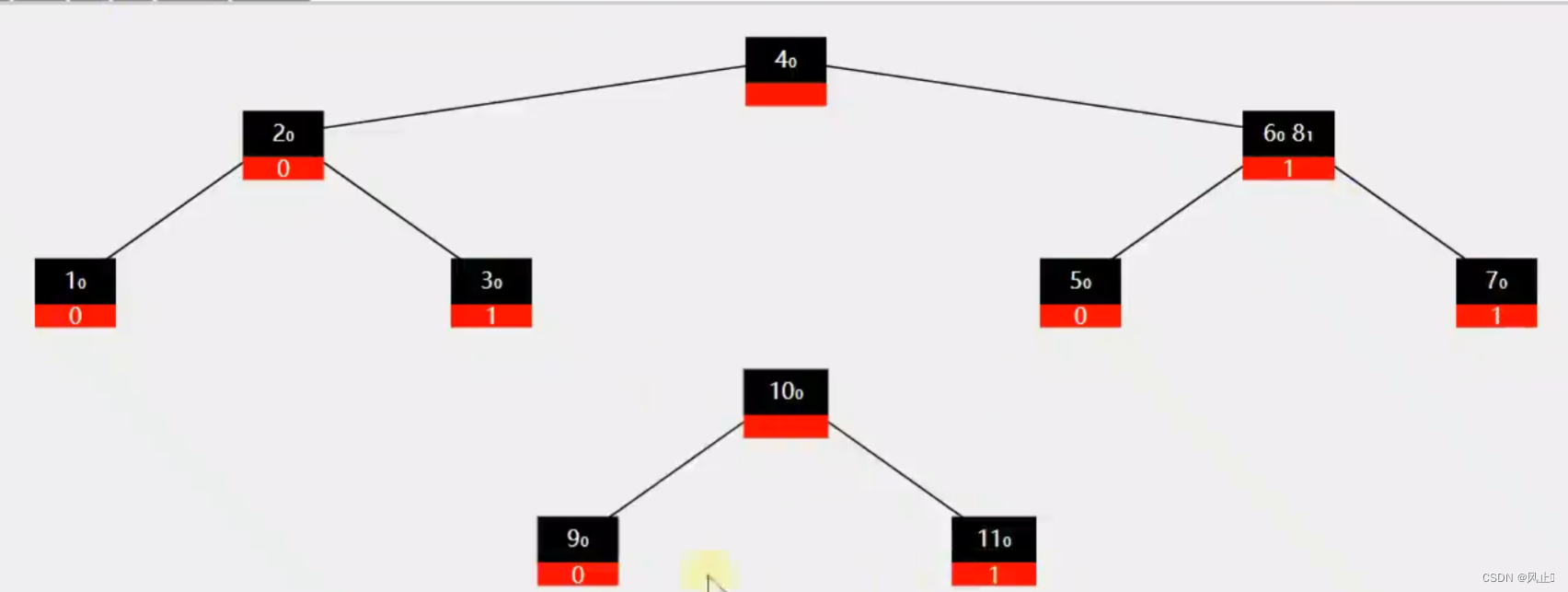
2.添加
-
首先,根据给定的关键字,从根节点开始向下搜索,找到合适的叶子节点。
-
在叶子节点中插入新的关键字。如果叶子节点未满,直接插入;否则,执行步骤3。
-
当叶子节点已满时,需要进行分裂操作。将当前节点一分为二,得到两个新的叶子节点,并选择一个关键字提升到父节点中。
-
如果父节点也已满,则重复步骤3,层层递归地向上分裂,直到找到一个非满节点或达到树的顶部。
-
完成插入操作后,需要更新祖先节点的关键字信息。如果某个节点发生了分裂,它提升的关键字需要插入到其父节点中,并根据大小顺序进行调整。
通过以上步骤,B树的插入操作可以保持树的平衡性。在插入过程中,B树会根据节点的容量进行自动调整,使得树的高度保持相对较低,从而确保各种操作的效率。
需要注意的是,在插入操作中可能会出现关键字重复的情况。对于B树来说,可以允许存在相同的关键字,而在查找操作时,会按照节点中关键字的大小顺序进行搜索。因此,在插入过程中需要根据具体需求来处理关键字重复的情况。
3.查找
-
从根节点开始,比较要查找的关键字与当前节点中的关键字。
-
如果找到了匹配的关键字,则表示查找成功,结束操作。
-
如果要查找的关键字小于当前节点的最小关键字,则进入当前节点的左子树进行继续查找。
-
如果要查找的关键字大于当前节点的最大关键字,则进入当前节点的右子树进行继续查找。
-
重复步骤 3 和 4,直到找到匹配的关键字或者到达叶子节点。
-
如果到达叶子节点仍然没有找到匹配的关键字,则表示查找失败,结束操作。
在B树的查找过程中,关键字的比较会指导搜索方向,通过不断地按照关键字的大小顺序向下搜索,可以快速地找到目标关键字或者判断其不存在。
需要注意的是,B树中允许存在相同的关键字,因此在查找操作中,如果存在多个相同的关键字,可以根据具体需求选择返回其中一个或全部。此外,B树的查找操作具有较好的平均时间复杂度,可以在较短的时间内完成查询。
3.代码实现
1.准备工作
//节点类
class BTreeNode {
// B树的阶数
int t;
List<Integer> keys;//关键字
List<BTreeNode> childNodes;//孩子
boolean leaf;//判断节点是否是叶子结点
public BTreeNode(int t, boolean leaf) {
this.t = t;
this.leaf = leaf;
this.keys = new ArrayList<>();
this.childNodes = new ArrayList<>();
}
}2.升序遍历树
public void traverse() {
int i;
for (i = 0; i < keys.size(); i++) {
if (!leaf) {
//去索引为i的孩子里面继续找
childNodes.get(i).traverse();
}
System.out.print(keys.get(i) + " ");
}
//最后还剩一个关键字的孩子节点
if (!leaf) {
childNodes.get(i).traverse();
}
}3.查找值所在的位置
public int search(int key) {
int i = 0;
//先找到比值小和等的节点 然后小的递归找孩子
while (i < keys.size() && key > keys.get(i)) {
i++;
}
//等的
if (i < keys.size() && key == keys.get(i)) {
return i;
} else if (leaf) {//都到叶子了还没找到就无了
return -1;
} else {
//递归继续去他的子节点找 小的
return childNodes.get(i).search(key);
}
}4.添加
public void insertNonFull(int key) {//处理节点未满的情况
int i = keys.size() - 1;
if (leaf) {//叶节点
while (i >= 0 && key < keys.get(i)) {//从后往前 找出比你小的那个i
i--;
}
keys.add(i + 1, key);//因为第i个位置是比你小的,所以你要插入后面一个
} else {//非叶节点
while (i >= 0 && key < keys.get(i)) {//找到要插入子节点的位置
i--;
}
//判断子节点是否需要分裂操作
if (childNodes.get(i + 1).keys.size() == (2 * t) - 1) {
splitChild(i + 1, childNodes.get(i + 1));
if (key > keys.get(i + 1)) {
i++;
}
}
//分裂完毕 或者 不需要分裂 递归插入
childNodes.get(i + 1).insertNonFull(key);
}
}5.分裂
public void splitChild(int i, BTreeNode y) {//处理节点满的情况进行分裂操作
BTreeNode z = new BTreeNode(y.t, y.leaf);
keys.add(i, y.keys.get(t - 1));//中间的上移
childNodes.add(i + 1, z);//创建新的孩子
for (int j = 0; j < t - 1; j++) {//后面的移动到新的里面
z.keys.add(j, y.keys.get(j + t));
}
if (!y.leaf) {//后半部分子节点移动到新的节点
for (int j = 0; j < t; j++) {
z.childNodes.add(j, y.childNodes.get(j + t));
}
}
//主要总用时为了情况没有用的部分
//获取被拆分节点后半部分的关键字和子节点部分。
y.keys.subList(t - 1, y.keys.size()).clear();
//方法用于删除列表中的元素(获取完删除)
y.childNodes.subList(t, y.childNodes.size()).clear();
}
}6.遍历查询
class BTree {
BTreeNode root;//根节点
int t;//树中的最小度数
//指定默认树的度数是2
public BTree() {
this(2);
}
public BTree(int t) {
this.root = null;
this.t = t;
}
//遍历树
public void traverse() {
//树不为空就可以遍历
if (root != null) {
root.traverse();
}
}
//查找节点的位置
public int search(int key) {
if (root != null) {
return root.search(key);
}
return -1;
}
//插入节点
public void insert(int key) {
if (root == null) {
root = new BTreeNode(t, true);
root.keys.add(0, key);
} else {
if (root.keys.size() == (2 * t) - 1) {
BTreeNode s = new BTreeNode(t, false);
s.childNodes.add(0, root);
s.splitChild(0, root);
int i = 0;
if (s.keys.get(0) < key) {
i++;
}
s.childNodes.get(i).insertNonFull(key);
root = s;
} else {
root.insertNonFull(key);
}
}
}
}