暴力递归到动态规划(二)
- 背包问题
- 递归版本
- 动态规划
- 数字字符串改字母字符串
- 递归版本
- 动态规划
- 字符串贴纸
- 递归版本
- 动态规划
**特别需要注意的是 我们使用数组之前一定要进行初始化 不然很有可能会遇到一些意想不到的错误 比如说在Linux平台上 new出来的int数组会初始化为0 但是在leetcode网页上默认初始化确不是0 博主因为这个错误找了好久 **
由于缓存法(记忆化搜索)实在是太简单了 所以说从本篇博客开始 我们直接从递归到完整的动态规划 不再经历缓存法
背包问题
递归版本
现在给我们两个数组 一个数组表示货物的重量 一个数组表示货物的价值 它们的下标一一对应切一定大于等于0
现在给定我们一个参数bag 表示我们背包能够承受重量的最大值 现在要求背包能够装的价值的最大值
我们的思考过程如下
我们设置函数的意义是 从第index件货物开始拿 我们能拿进背包的最大价值
首先想base case
- 如果此时背包的大小小于0 则说明背包无法装下任何货物 (背包大小可以为0 因为有可能货物的重量为0)
- 如果index等于数组的长度 则说明没有任何货物了 返回0
之后我们写出的代码如下
int process(vector<int>& w , vector<int>& v , int index , int bag)
{
if (bag < 0 )
{
return 0;
}
if (index == static_cast<int>(w.size()))
{
return 0;
}
int p1 = process(w , v , index + 1 , bag);
int p2 = v[index] + process(w , v , index + 1 , bag - w[index]);
return max(p1 , p2);
}
但是这里我们的base case其实是有问题的
因为如果我们只有一个货物 即使p2超重了 我们仍然会走p2这条分支 并且会拿走这个超重的货物 这显然是不合适的 所以说我们需要改写下base case和选择代码
修改后的代码如下
int process(vector<int>& w , vector<int>& v , int index , int bag)
{
if (bag < 0 )
{
return -1;
}
if (index == static_cast<int>(w.size()))
{
return 0;
}
int p1 = process(w , v , index + 1 , bag);
int p2 = 0;
int next = process(w , v ,index + 1 , bag - w[index]);
if (next != -1)
{
p2 = v[index] + next;
}
return max(p1 , p2);
}
动态规划
我们观察下原函数
process(vector<int>& w , vector<int>& v , int index , int bag)
变化的参数只有index 和 bag 所以说我们只要建立index和bag的二维表就能解决问题
我们首先看每个格子依赖于什么
int p1 = process(w , v , index + 1 , bag);
int p2 = 0;
int next = process(w , v ,index + 1 , bag - w[index]);
观察上面的两个函数 我们就能得到下图
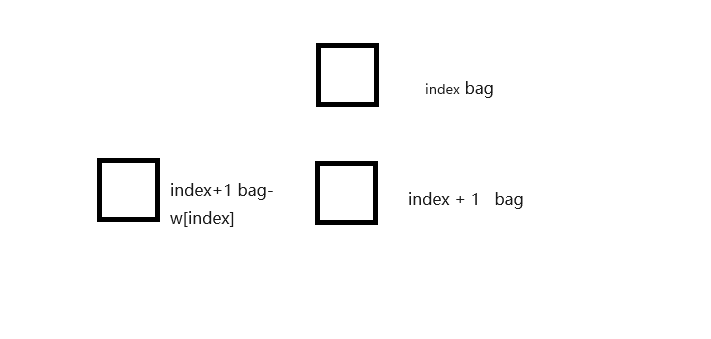
每个格子依赖于它下面的两个格子 (如果存在的话)
所以说我们的动态规划要从最下面开始 从左往右填
for (int dpindex = w.size() - 1 ; dpindex >= 0 ; dpindex--)
{
for(int dpbag = 0; dpbag <= bag ; dpbag++)
{
int p1 = dp[dpindex + 1][dpbag];
int p2 = 0;
if (dpbag - w[dpindex] >= 0)
{
p2 = v[dpindex] + dp[dpindex+1][bag - w[dpindex]];
}
dp[dpindex][dpbag] = max(p1 , p2);
}
}
这样子我们的动态规划代码就完成了
数字字符串改字母字符串
递归版本
我们规定 1数字代表 ‘a’ 2数字代表 ‘b’ … … 以此类推
现在给你一串数字字符 要求你返回能改成字母字符串的最大解法
函数表示如下
int process(string& str , int index)
该函数的意义是 从str的index位置开始 按题目要求有的最大解法
我们首先来想base case
- 如果index此时走到了str.size() 此时就是一个空串 空串也是一种解法 再拼接上前面的字符串 就是一种完整的解法
- 如果index单独走到了数字0的位置 那么此时就没有解法了
之后我们来想普遍情况 当前字符单独转化 ? 还是当前字符 + 下面一个字符转化 ?
当然如果是当前字符 + 下面一个字符转化的话我们要考虑一些特殊情况
代码表示如下
int process(string& str , int index)
{
if (index == static_cast<int> (str.length()))
{
return 1;
}
if (str[index] == '0')
{
return 0;
}
// need cur
// need cur + 1 ?
int p1 = process(str , index + 1);
int p2 = 0;
if (index + 1 < static_cast<int>(str.length()) && (str[index] - '0') * 10 + (str[index+1] - '0') < 27 )
{
p2 = process(str , index + 2);
}
return p1 + p2;
}
动态规划
我们发现 递归函数中只依赖于一个参数index
int process(string& str , int index)
于是乎我们可以建立一张一维表
再通过递归函数看下依赖关系
int p1 = process(str , index + 1);
int p2 = 0;
if (index + 1 < static_cast<int>(str.length()) && (str[index] - '0') * 10 + (str[index+1] - '0') < 27 )
{
p2 = process(str , index + 2);
}
我们能够得到下图
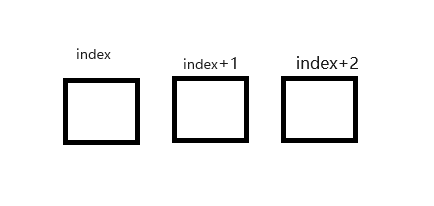
此时index + 2 不一定依赖 我们只需要加上一点判断条件即可
字符串贴纸
现在给定一个字符串str 给定一个字符串类型的数组arr 出现的字符全部是小写的英文字母
arr每一个字符串 代表一张贴纸 每种贴纸有无限多个 你可以把单个字符剪开使用 目的是拼出来str来返回需要至少多少张贴纸 返回一个最小值
例子: str = “babac” arr = {“ba” , “c” ,“abcd”}
至少需要两张贴纸 “abcd” “abcd”
递归版本
我们这么定义递归函数
int process(vector<string> stickers , string target)
这个函数的含义是 告诉我们贴纸的数量 告诉我们目标字符串 要求我们返回一个最小值
首先想base case
如果说target为空串了 此时我们只需要返回0即可
if (target.size() == 0)
{
return 0;
}
完整递归函数如下
int process(vector<string>& stickers , string target)
{
if (target.size() == 0)
{
return 0;
}
int Min = INT32_MAX;
for (auto first : stickers)
{
string rest = strminus(target , first);
if (rest.length() != target.length())
{
Min = min(Min , process(stickers , rest));
}
}
Min = Min + (Min == INT32_MAX ? 0 : 1);
return Min;
}
我们设置一个int类型的值 Min 作为一个系统最大值
之后遍历整个贴纸数组 看看贴纸数组中的字符能不能减少目标target
如果能 我们就继续递归下去 让递归函数给我们一个最大值 如果不能我们就继续遍历下一个贴纸
最后我们看看Min是不是还是系统最大值 如果是就直接返回 如果不是 我们就让Min+1之后返回 (因为此时我们只是得到了去除第一张贴纸之后的最小值 所以说最后要加一)
动态规划
我们首先看原函数 影响它的参数是什么
int process(vector<string>& stickers , string target)
我们发现只有一个target字符串在变化 但是我们对于字符串的变化是很难进行操作的
所以说对于这一题的动态规划我们采用记忆化搜索的方案
多加一个参数 map<string , int> 每次得到数据之前先把数据填进去即可
代码表示如下
int process(vector<string>& stickers , string target , map<string , int>& dp)
{
if (dp.find(target) != dp.end())
{
return dp.find(target)->second;
}
if (target.size() == 0)
{
return 0;
}
int Min = INT32_MAX;
for (auto first : stickers)
{
string rest = strminus(target , first);
if (rest.length() != target.length())
{
Min = min(Min , process(stickers , rest , dp));
}
}
Min = Min + (Min == INT32_MAX ? 0 : 1);
dp[target] = Min;
return Min;
}