题目传送门

1：RMQ + 二分

RMQ 能找到一个数组在任意区间的最大值或者最小值，只需要在O(n)的时间复杂度下就能完成预处理。
紧接着想到单调性：枚举左端点，也就是先确定好左端点，右端点从左往右，a数组的最大值一定是在增大或者不变，b数组的最小值一定也是在减小或者不变，那么这样就有了单调性，联想到二分。

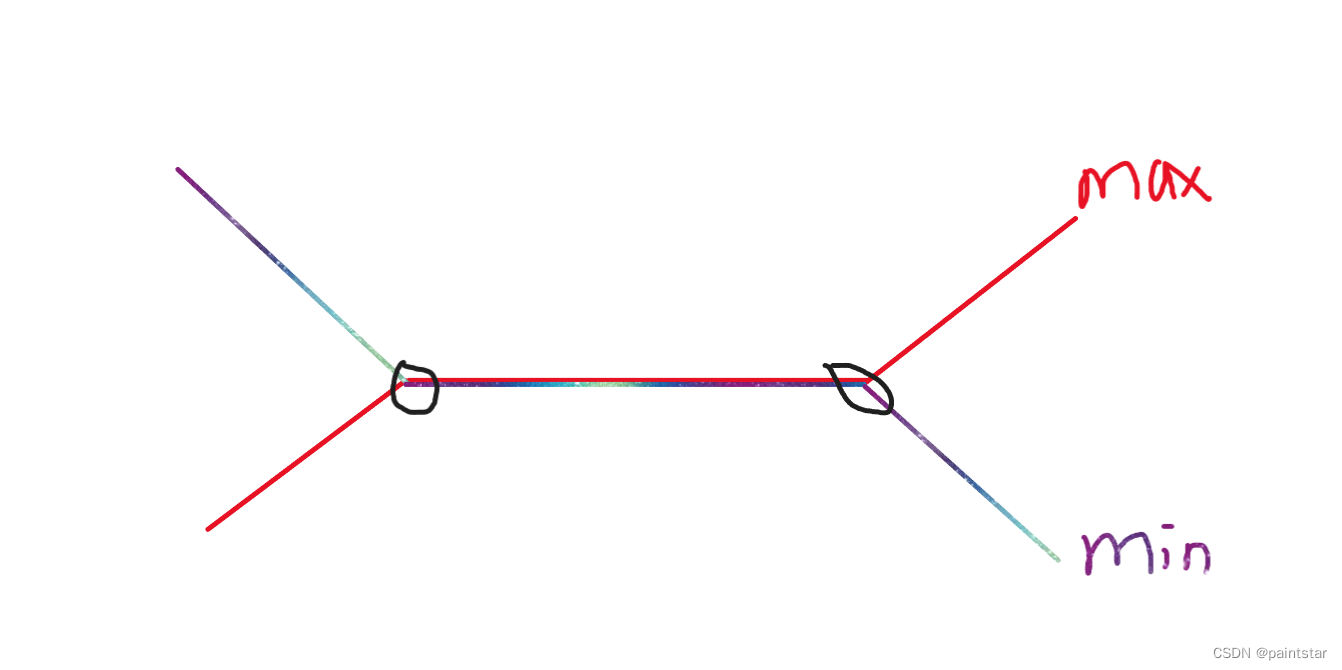
我们只需要二分出来这两个端点，然后算出中间长度，再累加就可以得到我们的答案了

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const int N = 2e5 + 10, M = 18;
int mx[N][M], mn[N][M], a[N], b[N];
int n;
void init()
{
    for (int i = n ;i>=1;i--)
    {
        for (int j = 0; j <= 17; j++)
        {
            if (i + (1 << j) - 1 > n) break;
            if (!j) mx[i][j] = a[i];
            else mx[i][j] = max(mx[i][j - 1], mx[i + (1 << j - 1)][j - 1]);
        }
    }
    for (int i = n; i >= 1; i--)
    {
        for (int j = 0; j <= 17; j++)
        {
            if (i + (1 << j) - 1 > n) break;
            if (!j) mn[i][j] = b[i];
            else mn[i][j] = min(mn[i][j - 1], mn[i + (1 << j - 1)][j - 1]);
        }
    }
}
int query_max(int l, int r)
{
    int len = r - l + 1;
    int tmp = log(len) / log(2);
    return max(mx[l][tmp], mx[r - (1<<tmp) + 1][tmp]);
}
int query_min(int l, int r)
{
    int len = r - l + 1;
    int tmp = log(len) / log(2);
    return min(mn[l][tmp], mn[r - (1 << tmp) + 1][tmp]);
}
bool check1(int l,int r)
{
    int x = query_max(l, r);
    int y = query_min(l, r);
    if (x >= y)return 1;
    else return 0;
}
bool check2(int l, int r)
{
    int x = query_max(l, r);
    int y = query_min(l, r);
    if (x > y)return 1;
    else return 0;
}
void solve()
{
    ll ans = 0;
    for (int i = 1;i <= n; i++)
    {
        int l = i, r = n;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (check1(i,mid)) r = mid;
            else l = mid + 1;
        }
        if (query_max(i, l) == query_min(i, l))
        {
            int t = l;
            int r = n;
            while (l < r)
            {
                int mid = l + r >> 1;
                if (check2(i, mid)) r = mid;
                else l = mid + 1;
            }
            if(l==n && query_max(i,l) == query_min(i,n)) l++; //这里如果按照我这样二分的话
            //要加个特判，因为我这里二分是找到第一个query_max(i,l) > query_min(i,n) 的数
            //可是如果找不到的话，就会返回n，这样的话就要l++，取到n+1
            ans += (ll)l - t;
        }
        
    }
    cout << ans << endl;
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];
    init();//RMQ预处理
    solve();
    return 0;
}

2：单调队列：

我们还可以采取前后单调队列的方法来做，这里我们枚举终点，做两个单调队列
一个单调队列记录a数组最大值下标，一个记录b数组最小值下标（队列里的第一个数就是该值的下标）
我们需要找到第a数组最大值与b数组最小值相等，也就是我们要从队列从前往后丢数出去，丢到队列1的最大值<=队列2的最小值为止。
如果实行呢？我们用一个 j 从 j 到 i 枚举，并且同时判断最大值和最小值的情况就可以了
这里要理解的是j是一步一步从左往右枚举，但是队列因为存储的是下标所以是跳着进行的
到最后满足条件的时候队列1的第一个值的下标和队列2的第一个值的下标距离 j 会有一段距离
而这二者的距离的min值就是我们需要进行累加的答案。
这里其实也满足单调性，每组数据一定只能找得到一次最大值和最小值相等，对于重复情况只需要在建立单调队列的时候只记录到最后一个值的下标就好了。

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define ll long long 
const int N = 2e5 + 10;
int a[N];
int b[N];
int q1[N], q2[N];
void solve()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];
	int h1 = 1, h2 = 1, t1 = 0, t2 = 0;
	ll ans = 0;
	for (int i = 1,j = 1; i <= n; i++)
	{
		while (h1 <= t1 && a[i] >= a[q1[t1]]) t1--;
		while (h2 <= t2 && b[i] <= b[q2[t2]]) t2--;
		q1[++t1] = i, q2[++t2] = i;
		while (j <= i && a[q1[h1]] > b[q2[h2]])
		{
			j++;
			if(h1 <= t1 && q1[h1] < j) h1++;
			if(h2 <= t2 && q2[h2] < j) h2++;
		}
		if (h1<=t1 && h2<=t2 && a[q1[h1]] == b[q2[h2]]) ans +=(ll) min(q1[h1], q2[h2]) - j + 1;
	}
	cout << ans << endl;
}
int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	int T;
	//cin >> T;
	T = 1;
	while (T--)
	{
		solve();
	}
	return 0;
}