目录
前言
哈夫曼树的实现
1.储存结构
2.创建初始化哈夫曼树
3.完整哈夫曼树创建
4.计算总权值
哈夫曼编码
完整代码
前言
前面我们学习过了哈夫曼树和哈夫曼编码的基础知识(链接:哈夫曼树哈夫曼编码必知必会知识_Gretel Tade的博客-CSDN博客,如果没了解过哈夫曼树的话建议看看这个),那么这一节我们就学习怎么去通过代码的方式实现哈夫曼树和哈夫曼编码的功能,下面一起来看看。
哈夫曼树的实现
1.储存结构
哈夫曼树可以去通过顺序结构来储存,其物理形式是数组,逻辑结构是一棵二叉树(有点类似堆),当然也可以去通过链式结构来去实现,只是哈夫曼树一般没有增删改查的操作,也就是创建了哈夫曼树就进行直接使用,所以不需要去通过动态空间的方式来进行链式储存。其结构如下所示:
typedef char Datatype;
//节点
typedef struct {
Datatype data;//储存数据
int weight; //权重
int par, left, right;//指向节点
}Node,*Hufftree;
2.创建初始化哈夫曼树
创建一个初始化的哈夫曼树,首先按照要求,顺序结构的哈夫曼树的第一个节点是为空的,不储存任何数据,从第二个位置开始储存数据。虽然要想创建一个n个节点的哈夫曼树其总节点为2n-1,但是由于第一个节点不储存任何数据,那就需要申请2n个节点空间。根据顺序结构的特性,我们可以把第1~n个数组节点作为叶子节点,然后第n+1~2n-1个节点作为叶子节点的父节点。代码如下:
//创建空哈夫曼树初始化
Hufftree Create_nulltree(int* w,Datatype* data,int n)
{
Node* H = (Hufftree)malloc(sizeof(Node)*(2*n));//申请2n个空间
if (!H)
{
printf("ERROR\n");
exit(-1);
}
//初始化指向节点为-1
for (int i = 1; i <= 2 * n - 1; i++) {
H[i].par = H[i].left = H[i].right = -1;
}
//赋值节点数据
for (int i = 1; i <=n; i++) {
H[i].weight = w[i-1];
H[i].data = data[i-1];
}
return H;
}
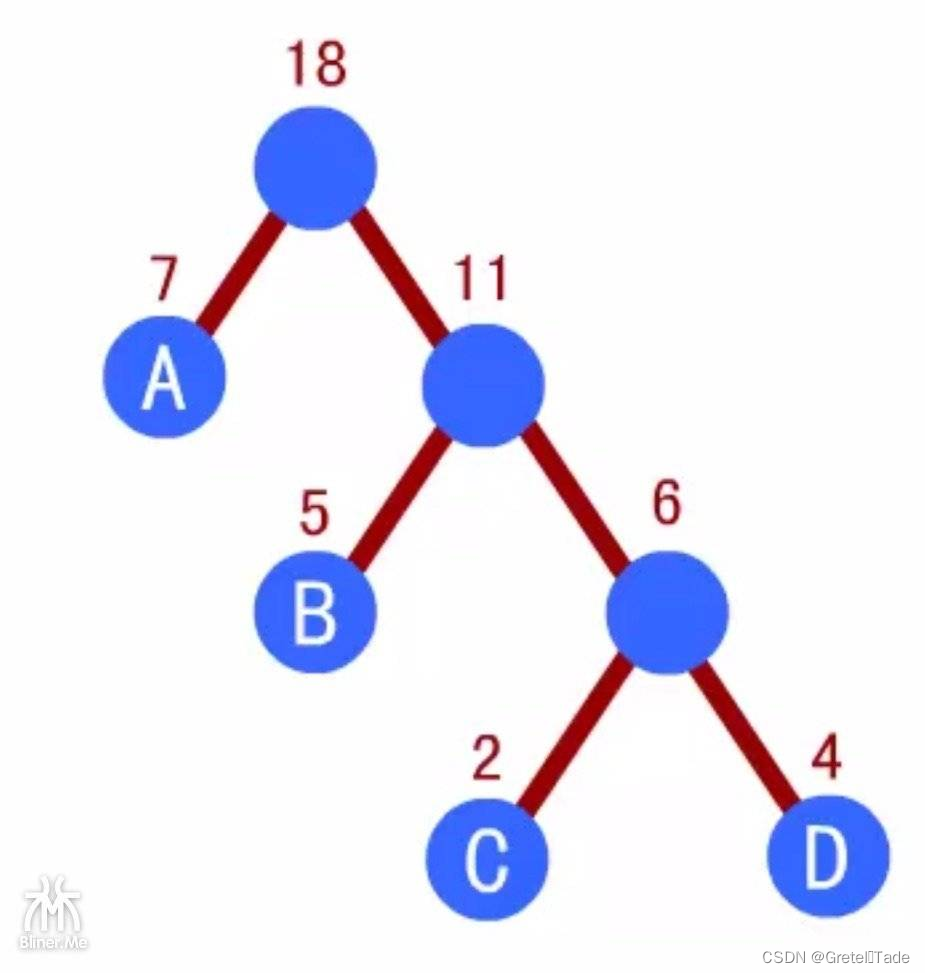
比如给定节点{A,B,C,D},其权重分别为{7,5,2,4},那么创建的哈夫曼树结构应该是如下所示,但是创建了一个初始化的树,我们还需要把这些叶子节点的父节点权重给补填上去,那才能是一个完整的哈夫曼树。
3.完整哈夫曼树创建
我们都知道,哈夫曼树的每一个根节点权是等于两个叶子节点相加而来的,那么由此我们可以按照以下的方法来构造哈夫曼树
构造过程如下:
1、给定n个权值为{W1,W2,W3……Wn}的节点,构造n棵只有一个叶子节点的二叉树,从而得到一个二叉树集合F={T1,T2,T3……Tn}
2、在F中选取根结点权值最小和依次最小的两个二叉树作为左右子树,构造为一个新的二叉树,这个二叉树的根节点就是左右子树根节点权值之和
3、在集合F中删除作为左右子树的二叉树,并且把刚刚新建立的二叉树放入到集合F中去
4、重复2、3步骤,当F中只剩下一棵二叉树的时候,这个二叉树就是要建立的哈夫曼树,创建完成。
//构建完整哈夫曼树
void Create_hufftree(Hufftree H, int n) {
assert(H);
if (n <= 1)
return;
for (int i = n + 1; i <= 2 * n - 1; i++) {//对顺序表后面n+1~2n-1节点进行操作
//初始化在这个过程中要用的数据
int lmin = 32767;//第一小的权值
int rmin = 32767;//第二小的权
int lnode = -1;//左边最小值
int rnode = -1;//右边最小值
//对原来有了的节点和新创建的父节点进行挑选操作
for (int j = 1; j <= i - 1; j++) {
if (H[j].par == -1) {//筛选,父节点为空的节点处理
if (H[j].weight < lmin) {
rmin = lmin;
rnode = lnode;
lmin = H[j].weight;
lnode = j;
}
else if (H[j].weight < rmin) {
rmin = H[j].weight;
rnode = j;
}
}
}
//构建树过程,此时lmin是当前最小权,rmin是第二小的权
H[lnode].par = H[rnode].par = i;
H[i].left = lnode;
H[i].right = rnode;
H[i].weight = H[lnode].weight + H[rnode].weight;
}
}4.计算总权值
要想计算总权值,按照哈夫曼树的权值计算方法,把节点权值乘上路径的长度,但是我们既然构建了哈夫曼树,我们只需要把所有除叶子节点的其他节点权值加起来就行了。比如上面图片那个哈夫曼树,其权值计算是:7+5*2+4*3+2*3=35。那我们把父节点加起来:6+11+18=35,看结果是一样的,具体的想想都很容易理解的,直接上代码:
//计数权值
int WPL(Hufftree H,int n) {
int sum = 0;
for (int i = n + 1; i <= 2 * n - 1; i++) {
sum += H[i].weight;
}
return sum;
}哈夫曼编码
有了哈夫曼树那就要给这个树进行编码,其顺序表有效节点是从1~n,所以我们要申请创建的字符串数组也应该是n+1个的,跟哈夫曼树节点一样数组的第0个位置是不用的。
代码书写思路:
既然知道了哈夫曼编码的要求,也有了哈夫曼树,那我们怎么去写这个代码呢?我们可以这样子,从哈夫曼树的叶子节点开始向上遍历,用一个临时字符串储存遍历到的结果,这个老临时字符串开始的位置是从最后一位开始,判断如果此时这个节点那么就在这个临时字符串放入字符'0',反之放入'1',然后临时字符串储存位置向前移动一位,哈夫曼树向上移动一个节点……最后就可以完成这个节点的哈夫曼编码。代码如下:
//哈夫曼编码
char** Create_huffcode(Hufftree H, int n) {
char** code = (char**)malloc(sizeof(char*) * (n+1));//创建哈夫曼编码储存字符串
char* cd = (char*)malloc(sizeof(char) * n);//创建临时字符串空间储存字符串
cd[n - 1] = '\0';
int start, k, p;
//方法是从子节点开始往上遍历,如果是左节点的话字符串cd就存入一个字符‘0’,反之放入‘1’,到最后的根节点,就遍历完成
for (int i = 1; i <= n; i++) {//对每一个节点进行创建哈夫曼编码
//初始化
start = n - 1;//临时字符串从最后一个字符开始
k = i;
p = H[i].par;//标记子节点的父节点
while (p!=-1) {//到达根节点结束
start--;
if (H[p].left == k)
cd[start] = '0';
else
cd[start] = '1';
//依次往上走
k = p;
p = H[k].par;
}
code[i] = (char*)malloc(sizeof(char) * (n-start));
strcpy(code[i], &cd[start]);//复制拷贝
}
free(cd);//释放临时空间
return code;
}
完整代码
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<assert.h>
typedef char Datatype;
//节点
typedef struct {
Datatype data;//储存数据
int weight; //权重
int par, left, right;//指向节点
}Node,*Hufftree;
//创建空哈夫曼树初始化
Hufftree Create_nulltree(int* w,Datatype* data,int n)
{
Node* H = (Hufftree)malloc(sizeof(Node)*(2*n));//申请2n个空间
if (!H)
{
printf("ERROR\n");
exit(-1);
}
//初始化指向节点为-1
for (int i = 1; i <= 2 * n - 1; i++) {
H[i].par = H[i].left = H[i].right = -1;
}
//赋值节点数据
for (int i = 1; i <=n; i++) {
H[i].weight = w[i-1];
H[i].data = data[i-1];
}
return H;
}
//构建完整哈夫曼树
void Create_hufftree(Hufftree H, int n) {
assert(H);
if (n <= 1)
return;
for (int i = n + 1; i <= 2 * n - 1; i++) {//对顺序表后面n+1~2n-1节点进行操作
//初始化在这个过程中要用的数据
int lmin = 32767;//第一小的权值
int rmin = 32767;//第二小的权
int lnode = -1;//左边最小值
int rnode = -1;//右边最小值
//对原来有了的节点和新创建的父节点进行挑选操作
for (int j = 1; j <= i - 1; j++) {
if (H[j].par == -1) {//筛选,父节点为空的节点处理
if (H[j].weight < lmin) {
rmin = lmin;
rnode = lnode;
lmin = H[j].weight;
lnode = j;
}
else if (H[j].weight < rmin) {
rmin = H[j].weight;
rnode = j;
}
}
}
//构建树过程,此时lmin是当前最小权,rmin是第二小的权
H[lnode].par = H[rnode].par = i;
H[i].left = lnode;
H[i].right = rnode;
H[i].weight = H[lnode].weight + H[rnode].weight;
}
}
//计算权值
int WPL(Hufftree H,int n) {
int sum = 0;
for (int i = n + 1; i <= 2 * n - 1; i++) {
sum += H[i].weight;
}
return sum;
}
//哈夫曼编码
char** Create_huffcode(Hufftree H, int n) {
char** code = (char**)malloc(sizeof(char*) * (n+1));//创建哈夫曼编码储存字符串
char* cd = (char*)malloc(sizeof(char) * n);//创建临时字符串空间储存字符串
cd[n - 1] = '\0';
int start, k, p;
//方法是从子节点开始往上遍历,如果是左节点的话字符串cd就存入一个字符‘0’,反之放入‘1’,到最后的根节点,就遍历完成
for (int i = 1; i <= n; i++) {//对每一个节点进行创建哈夫曼编码
//初始化
start = n - 1;//临时字符串从最后一个字符开始
k = i;
p = H[i].par;//标记子节点的父节点
while (p!=-1) {//到达根节点结束
start--;
if (H[p].left == k)
cd[start] = '0';
else
cd[start] = '1';
//依次往上走
k = p;
p = H[k].par;
}
code[i] = (char*)malloc(sizeof(char) * (n-start));
strcpy(code[i], &cd[start]);//复制拷贝
}
free(cd);//释放临时空间
return code;
}
int main() {
int w[] = { 7,2,4,5 };
Datatype data[] = { "ABCD" };
int n = sizeof(w) / sizeof(int);
Hufftree H = Create_nulltree(w, data,n);
Create_hufftree(H,n);
char** code = Create_huffcode(H, n);
printf("总权值为:%d\n", WPL(H,n));
for (int i = 1; i <= n; i++) {
printf("%c:", H[i].data);
printf("%s\n", code[i]);
}
}
以上就是本期的内容了,我们下次见!
分享一张壁纸: