Reference:

1. 搞懂神经辐射场 Neural Radiance Fields (NeRF)
2. 尽量简单易懂的讲清楚神经辐射场（Nerf）
3. Deep Dive into NeRF (Neural Radiance Fields)

NERF的目标是根据观察者(相机)的姿势来渲染高质量的图像。NeRF是神经渲染技术的一个例子——我们明确地控制场景的一个属性——观察者的姿势——以获得与该姿势相对应的渲染图像。该模型学习了一个连续的体积场景函数，它可以为空间中的任何体素分配颜色和体积密度。网络的权重被优化为对场景的表示进行编码，这样模型就可以很容易地呈现从空间中任何一点看到的新视图。可以把它想象成“蒸馏”或“压缩”一些3D空间的信息，例如你的公寓，到一个非常小的参数集(NeRF的参数)。

基本上介绍 NeRF 的文章都会介绍，NeRF 模型输出的是某条 Ray 上面的一个点，对这条 Ray 的所有点做积分，可以得到相应像素的 RGB 值，那么这个 Ray 是怎么来的？

首先，我们要明白这条 Ray 是什么--------它是由 相机/你的眼睛 发出，一直会穿过实际 3D 物体的一条虚拟的射线。如下图所示：

图中的 Image plane 就是我们最后想得到的图，我们要用 NeRF 找到 Image plane 上面每个像素的 RGB。

那么怎么找呢？
就是利用图中的箭头，也就是我们说的 Ray，首先使用 NeRF 找到箭头与 Volume Data 也就是 3D 物体的若干交点，然后对这些交点做积分就行了。

这里并不是眼睛能发出光，而是相反只能接收光。但因为光路是可逆的，再理解问题时，可能假设眼睛发光。

所以，一条 Ray 对应最终图片中的一个像素，而确定 Ray 的关键，就是要搞清楚相机的位姿，即 Ray 的原点，因为所有的 Ray 都是从相机 “发出” 的。

本文使用 tinynerf 讲述大致过程。

Step 1：相机 Rays 行进(ray marching)

输入：一组相机位姿 { x c , y c , z c , γ c , θ c } n \{x_c, y_c, z_c, \gamma_c, \theta_c\}_n {xc​,yc​,zc​,γc​,θc​}n​
输出：每个位姿的一束光线(a bundle of rays) { v o , v d } H × W × n \{\mathbf{v_o}, \mathbf{v_d}\}_{H\times W\times n} {vo​,vd​}H×W×n​

要搞清楚相机的位置和 Ray 的方向信息，得先建立坐标系，即全局坐标参考系(世界坐标)。

让我们看一下问题设置。我们想要渲染的对象位于点 $(0,0,0)$ (世界坐标)。物体被放置在一个 3D 场景中，我们称之为物体空间。摄像机固定在空间的位置 $(x_c,y_c,z_c)$。由于相机总是“瞄准”物体，我们只需要两个旋转参数来完全描述姿态：倾角和方位角 (γc，θc)(感觉这里写成倾角和方位角是有问题，因为这样仅考虑了 yaw 和 pitch 而放弃了 roll，理论上这是不可能的) $d_x$、$d_y$、$d_z$ 中任意两个，第三个通过叉乘求出，俗称“知二得三”。在数据集中，我们有 $n$ 对姿势，以及相应的地面真值图像。

在相机前面，我们放置成像平面。直观地说，图像平面是我们的“画布”，这是所有来自光线的3D信息将被聚合到渲染2D图像(3D到2D投影)的地方。图像平面大小为 $H\times W$。

显示前五个相机姿势及其各自的图像平面，所有的相机都“瞄准”物体空间

现在，我们从相机“拍摄”一束光线，通过图像平面的每个像素，得到每个位姿 $H\times W$ 光线。每条射线都由两个向量描述：

1. ${\mathbf{v}}_{\mathbf{o}}$，表示射线原点的向量。注意 ${\mathbf{v}}_{\mathbf{o}}=(x_o,y_o,z_o)=(x_c,y_c,z_c)$
2. ${\mathbf{v}}_{\mathbf{d}}$，一个标准化的向量，它指定了射线的方向。

参数方程 $P={\mathbf{v}}_{\mathbf{o}}+t\ast {\mathbf{v}}_{\mathbf{d}}$ 定义了射线上的任意点。因此，为了进行“光线行进”，我们将 $t$ 参数变大(从而扩展我们的光线)，直到光线到达物体空间中某个有趣的位置。

与上面的图像相同，但现在我们从每个相机(观察者)投射光线

上面描述的这种类型的光线追踪过程称为反向追踪。这是因为我们遵循光线从相机到物体的路径，而不是从光源到物体的路径。

Step 2：收集查询点

输入：每个位姿的一束光线(a bundle of rays) { v o , v d } H × W × n \{\mathbf{v_o}, \mathbf{v_d}\}_{H\times W\times n} {vo​,vd​}H×W×n​
输出：一组3D查询点 { x p , y p , z p } n × m × H × W \{x_p,y_p,z_p\}_{n×m×H×W} {xp​,yp​,zp​}n×m×H×W​

在计算机图形学中，3D 场景通常被建模为一组称为体素的微小的、离散的区域“立方体”。当光线“飞过”场景时，它将穿过空间中的大量点。这些点中的大多数代表“空”，然而，有些可能落在物体体积本身。后一点对我们来说非常有价值——它们让我们对场景有了一些了解。为了渲染图像，我们将查询训练好的神经网络，一个点，场景体积的一小部分，是否属于物体，更重要的是，它具有哪些视觉属性。我们可以直观地看到沿着一条射线的采样点不是微不足道的。如果我们对很多不属于物体空间的点进行采样，我们将得不到任何有用的信息。尽管如此，如果我们只采样一些高体积密度区域(体积密度分布模式周围的点)，我们可能会错过其他一些感兴趣的区域。

在我们的示例中，我们沿着射线均匀采样(对于每条射线我们采样 $m$ 个点)。但为了更好的性能，作者使用“分层体积采样”来按比例分配样本，以达到最终渲染的预期效果。要了解更多细节，请参考原文。

对于每个位姿，我们显示一条射线(否则图像将是一个完全混乱)，连同它的采样点。

Step 3：将查询点投射到高维空间(位置编码)

输入：一组 3D 查询点 { x p , y p , z p } n × m × H × W \{x_p,y_p,z_p\}_{n×m×H×W} {xp​,yp​,zp​}n×m×H×W​
输出：一组嵌入到 $d$ 维空间 { x 1 , x 2 ， … ， x d } n × m × H × W \{x_1,x_2，…，x_d\}_{n\times m\times H\times W} {x1​,x2​，…，xd​}n×m×H×W​ 的查询点

一旦我们收集了每条射线的查询点，我们就有可能准备好将它们输入神经网络。然而，本文的作者认为，在推理步骤之前，将查询点映射到高维空间是有益的。这个映射是非常特殊的——它使用了一组高频函数。

众所周知 On the Spectral Bias of Neural Networks，神经网络(毕竟是通用函数逼近器)在逼近低频函数方面比高频函数要好得多：

[…] 我们强调了深度网络对低频函数的学习偏差——即全局变化而没有局部波动的函数——这表现为频率依赖的学习速度。直观地说，这个特性与过度参数化网络优先学习跨数据样本泛化的简单模式的观察结果是一致的。

换种说法解释为什么要引入位置编码：传统的 MLP 网络不善于学习高频数据信息，但是基于颜色的纹理信息都是高频的，如果直接使用 MLP 学习，会导致学得纹理的表面相当模糊。因此引入了位置编码，让 MLP 同时学习高低频信息，提升清晰度。

这一观察结果在 NeRF 的背景下非常重要。高频特征，如颜色、详细的几何形状和纹理，使图像对人眼来说更加敏锐和生动。如果我们的网络无法表示这些属性，那么生成的图像可能看起来黯淡或过于平滑。然而，随着时间的推移，网络改善的方式类似于观察一个物体从雾中出现。首先，我们看到一个大致的轮廓，粗糙的轮廓和主色调。稍后我们可能会注意到对象的细节、纹理和更细粒度的元素。

从右起:1)我们想要生成的图像2)用位置编码渲染的图像3)忽略该图像;4)没有位置编码的渲染图像。缺少位置编码会导致渲染后的图像暗淡、过度平滑。 作者声称，在将输入传递给网络之前， 使用高频函数将输入映射到更高维度的空间，可以更好地拟合包含高频变化的数据。在我们的例子中，我们使用两个函数 -sine 和 -cosine 来嵌入高维空间中的点。

位置编码机制的可视化示例。

上图是随机点 $p=[-0.039,-1.505,-1.316]$ 的映射的图形表示，使用编码函数 $\gamma (p)$：
$\gamma (p)=(sin(\pi p),cos(\pi p),sin(2\pi p),cos(2\pi p))=([-0.039,-0.998,-0.968],[0.999,0.065,0.251],[-0.079,-0.123,-0.486],[0.997,-0.992,-0.874])$。可以看到坐标被映射成了 $4$ 组数。

Step 4：神经网络推理和体渲染

神经网络推理

输入：一组 3D 查询点(位置编码后的) { x p , y p , z p } n × m × H × W \{x_p,y_p,z_p\}_{n×m×H×W} {xp​,yp​,zp​}n×m×H×W​
输出：每个查询点的 RGB 颜色和体积密度 { R G B , σ } n × m × H × W \{RGB, \sigma\}_{n×m×H×W} {RGB,σ}n×m×H×W​

我们将查询点的表示形式输入 NeRF 网络。网络返回每个点的 RGB 值(范围从 $0$ 到 $1$ 的三个值的元组)和体积密度(一个单一的正整数)。这允许我们计算每条射线的体积密度剖面。

单条射线的密度分布图，图上的颜色即为查询点的 RGB 颜色。这个配置文件来自于学习代表黄色乐高推土机的训练网络。我们可以看到光线最初“飞过”未被体素占据的空间(前五个点)。然后，一旦它碰到一些红色体素(我假设它是车辆顶部的红色信标)，它就开始“穿透”推土机驾驶室的体积(体积密度是非零值)。物体内部的大多数体素是黄色、橙色和棕色的。最后，射线离开物体(并且体积密度返回到大约为零)。

体渲染

输入：一组 3D 查询点(经过位置编码) + 它们的体积轮廓 + RGB值 { x 1 , x 2 , … , x d , R G B ， σ } n × m × H × W \{x_1, x_2, …, x_d,RGB，σ\}_{n×m×H×W} {x1​,x2​,…,xd​,RGB，σ}n×m×H×W​

输出：一组渲染图像(每个姿态一个) { H , W } n \{H,W\}_n {H,W}n​

接下来，我们可以将沿射线的体积密度剖面转换为像素值。然后我们对图像中的每个像素重复这个过程。

为了从一条光线上的所有点聚集信息，我们使用了计算机图形学中的经典方程——渲染方程。它是一个积分方程，其中在几何光学近似下，离开一个点的平衡辐射被给出为发射和反射辐射的总和。

在 NeRF 的背景下，因为我们使用直射线并使用样本近似积分，所以这个看似复杂的积分可以简化为一个非常优雅的和。

我们计算沿着光线的所有点的所有RGB值的总和，通过光线从观察者飞到场景时在任何给定点停止的概率加权(参见原始论文中的公式3)。点的体积密度越高，光线在该点停留的概率就越高，因此该点的RGB值对渲染像素的最终RGB文件产生显著影响的概率也就越大。

建议关于 Scratchapixel网站 上的体积渲染。

计算损失

输入一组渲染图像(每姿态一张) $H,Wn$ 和一组地面真实图像(每姿态一张) { H , W } n g t \{H,W\}_n^{gt} {H,W}ngt​

输出 L2 输入之间的损耗，单个标量 { l } n \{l\}_n {l}n​

最后，我们通过比较渲染图像的像素与地面真实图像的像素来计算损失。然后我们反向传播这个损失来优化网络的权重。

渲染后的图像(左) 真值(右)

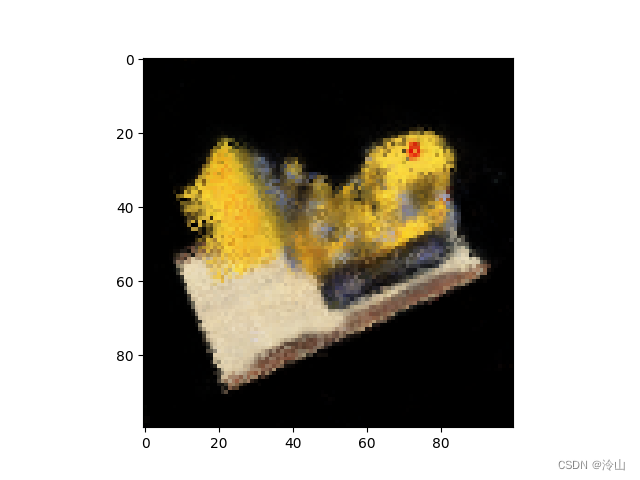
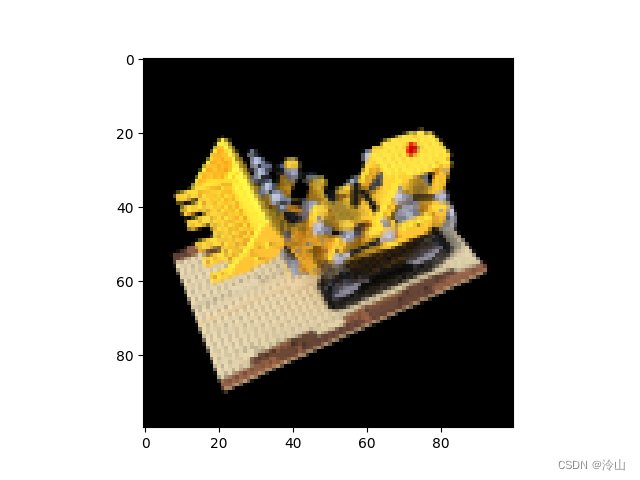
以及使用代码时生成的 gif：

训练 TinyNerf - NeRF的基本版本，具有最少的花里胡哨，例如没有分层体积采样