题目: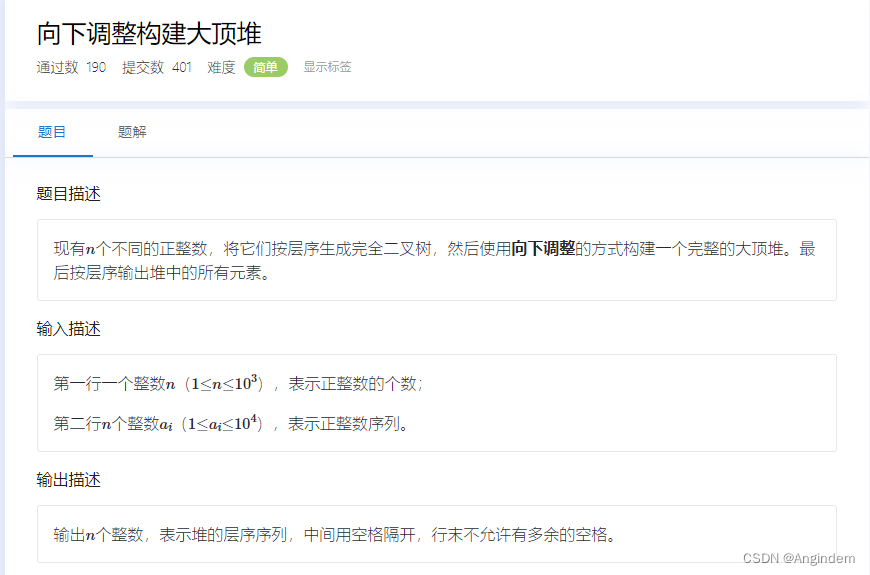
样例:
|
| 8 5 7 3 2 6 |
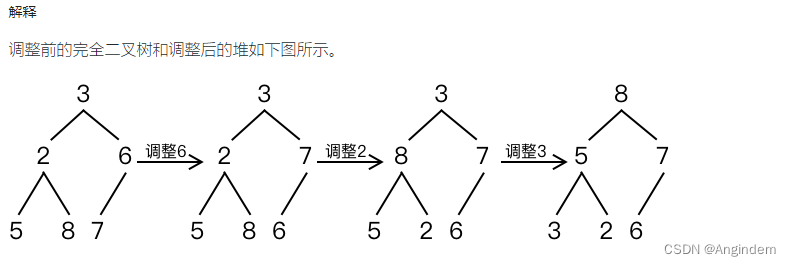
思路:
堆,是一颗完全二叉树,树中每个节点的值都不小于(或不大于)其左右孩子结点的值。
其中,
父结点大于或者等于孩子结点的值,称为大顶堆。
父结点小于或者等于孩子结点的值,称为小顶堆。
由于堆,是一颗完全二叉树,所以,我们可以将该完全二叉树压缩成 一维数组进行存储。
其中,第一个结点 存储于数组中的 1 号位,并且数组 i 号位 表示的结点的左孩子就是 2i 号位,而右孩子则是(2i + 1)号位。
向下调整堆,就是从 顶部的 根节点 向下调整到 叶子结点。
代码详解如下:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10,M = 500;
using PII = pair<int,int>;
int n;
umap<int,int>heap; // 可以用哈希表作为 heap ,即有效率,又可以根据题意的数组大小变化
inline void downAdjust(int low,int high)
{
int i = low,j = i * 2; // i 为欲调整的结点,由于是父结点开始调整所以是 i = low , j 为 左孩子
// j 没有到达叶子结点,就向下调整
while(j <= high)
{
// 如果存在右孩子,并且右孩子比左孩子大,我们调整右孩子
if(j + 1 <= high && heap[j + 1] > heap[j])
{
++j;
}
// 如果孩子结点 比 父结点 大 就向上调整
if(heap[j] > heap[i])
{
swap(heap[j] , heap[i]); // 交换结点数值
i = j; // 交换调整结点下标
j = i * 2; // 更新调整结点 的 孩子结点下标
}else break;
}
}
inline void solve()
{
cin >> n;
// 输入原始堆位
for(int i = 1;i <= n;++i) cin >> heap[i];
// 这里 n / 2 是 保证每个结点都是以其为父结点的子树中的权值最大的结点 进行向下调整
for(int i = n / 2;i;--i) downAdjust(i,n);
// 输出 调整后的堆
for(int i = 1;i <= n;++i)
{
if(i > 1) cout << ' ';
cout << heap[i];
}
}
signed main()
{
// freopen("a.txt", "r", stdin);
___G;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}