一、实验内容
实验内容包含要进行什么实验,实验的目的是什么,实验用到的算法及其原理的简单介绍。
1.1 手动实现前馈神经网络解决上述回归、二分类、多分类问题
分析实验结果并绘制训练集和测试集的loss曲线。
原理介绍:回归问题使用的损失函数为平方损失函数,二分类问题使用的损失函数为nn.BCEloss函数,多分类问题使用的损失函数为交叉熵损失函数nn.CrossEntropyLoss。三个问题的激活函数均为relu函数,函数表达式如下:
ReLU(x)={█(x x≥0@0 x<0)┤
1.2 利用torch.nn实现前馈神经网络解决上述回归、二分类、多分类问题
分析实验结果并绘制训练集和测试集的loss曲线。与手动实现不同的是需要设置优化器optimizer。
1.3 在多分类实验的基础上使用至少三种不同的激活函数
对比使用不同激活函数的实验结果。
原理介绍:使用了tanh、relu、leakyrelu三种激活函数。函数表达式如下:
tanh(x)=(exp(x)-exp(-x))/(exp(x)+exp(-x) )
LeakyReLU(x)={█(〖x 〗_ if x>0@γx if x≤0)┤
1.4 对多分类任务中的模型评估隐藏层层数和隐藏单元个数对实验结果的影响
使用不同的隐藏层层数和隐藏单元个数,进行对比实验并分析实验结果,对比至少三组。
1.5 在多分类任务实验中实现momentum、rmsprop、adam优化器
在手动实现多分类的任务中手动实现三种优化算法,并补全Adam中计算部分的内容
在torch.nn实现多分类的任务中使用torch.nn实现各种优化器,并对比其效果
1.6 在多分类任务实验中分别手动实现和用torch.nn实现L_2正则化
探究惩罚项的权重对实验结果的影响(可用loss曲线进行展示)。
原理介绍:在模型原损失函数基础上添加𝐿2范数惩罚项,通过惩罚绝对值较大的模型参数为需要学习的模型增加限制,来应对过拟合问题。带有𝐿2范数惩罚项的模型的新损失函数为:
l_0+λ/2n |w|^2
其中w是参数向量,l_0是模型原损失函数,n是样本个数,λ是超参数
1.7在多分类任务实验中分别手动实现和用torch.nn实现dropout
探究不同丢弃率对实验结果的影响(可用loss曲线进行展示)。
原理介绍:在前馈神经网络中,当使用dropout时,前馈神经网络隐藏层中的隐藏单元ℎ𝑖有一定概率被丢弃掉。在实验中设丢弃概率为p,那么有p的概率ℎ𝑖会被清零,有1−p的概率ℎ𝑖会除以1−p做拉伸,由此来定义进行dropout操作的函数。
1.8 对多分类任务实验中实现早停机制,并在测试集上测试
选择上述实验中效果最好的组合,手动将训练数据划分为训练集和验证集,实现早停机制,
并在测试集上进行测试。训练集:验证集=8:2,早停轮数为5.
二、实验设计
若实验内容皆为指定内容,则此部分则可省略;若实验内容包括自主设计模型等内容,则需要在此部分写明设计思路、流程,并画出模型图并使用相应的文字进行描述。
三、实验环境及实验数据集
简单介绍实验环境和涉及的数据集:
环境:
Python3.11+pytorch+pycharm
操作系统:Windows11
数据集:
1.回归任务数据集:单个数据集,大小为10000且训练集大小为7000,测试集大小为3000。数据集的样本特征维度p为500,且服从如下的高维线性函数:
y = 0.028 + ∑_(i=1)^P▒〖0.0056x_i 〗+σ
2.二分类任务数据集:两个数据集,每个数据集的大小均为10000且训练集大小为7000,测试集大小为3000。两个数据集的样本特征x的维度均为200,且分别服从均值互为相反数且方差相同的正态分布。两个数据集的样本标签分别为0和1。
3.多分类实验数据集:使用的是MNIST数据集。该数据集包含60000个用于训练的图像样本和10000个用于测试的图像样本。图像是固定大小(2828像素),其值为0到1,为每个图像都被平展并转换为784(2828)个特征的一维numpy数组。(用代码实现,运行时自动下载)
四、实验过程
4.1 手动实现前馈神经网络解决上述回归、二分类、多分类问题
(1).回归问题
首先,按要求创建数据集,并读取数据,将batch_size设置为32:
n_train,n_test=7000,3000
num_inputs=500
true_w, true_b = torch.ones(num_inputs, 1) * 0.0056, 0.028
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w)+true_b
labels += torch.tensor(np.random.normal(0, 0.001, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
batch_size = 32
dataset1 = torch.utils.data.TensorDataset(train_features,train_labels)
train_iter = torch.utils.data.DataLoader(dataset1,batch_size,shuffle=True)
dataset2 = torch.utils.data.TensorDataset(test_features,test_labels)
test_iter = torch.utils.data.DataLoader(dataset2,batch_size,shuffle=True)
定义模型参数并初始化:
num_outputs = 1
num_hiddens = 256
W1 = torch.tensor(np.random.normal(0,0.01,(num_hiddens,num_inputs)),dtype=torch.float)
b1 = torch.zeros(num_hiddens,dtype = torch.float)
W2 = torch.tensor(np.random.normal(0,0.01,(num_outputs,num_hiddens)),dtype=torch.float)
b2 = torch.zeros(num_outputs,dtype = torch.float)
params=[W1,b1,W2,b2]
for param in params:
param.requires_grad_(requires_grad = True)
因为有梯度计算,所以不能调用numpy库中的函数,根据函数表达式来定义relu激活函数:
def relu(x):
x[x <= 0] = 0
x[x > 0] = 1
return x
定义平方损失函数:
def squared_loss(y_hat, y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
定义随机梯度下降函数:
def sgd(params, lr):
for param in params:
param.data -= lr * param.grad
定义模型:
def net(X):
X=X.view((-1,num_inputs))
H = relu(torch.matmul(X, W1.t()) + b1)
return torch.matmul(H,W2.t())+b2
接下来定义模型训练函数,与实验一相同部分不再赘述,还需要添加绘制loss曲线的部分:
train_loss.append(train_l_sum/n)
test_loss.append(test_l)
plt.plot(x, train_loss, label="train_loss", linewidth=1.5)
plt.plot(x, test_loss, label="test_loss", linewidth=1.5)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.legend()
plt.show()
(2).二分类问题
按要求生成两个数据集,再分别使两个数据集的训练集合成一个作为实验的整个训练集,测试集同理:
#训练集
x0 = torch.normal(1*torch.ones(7000,200),1)
y0 = torch.zeros(7000)
x1 = torch.normal(-1*torch.ones(7000,200),1)
y1 = torch.ones(7000)
x_train = torch.cat((x0, x1), 0).type(torch.FloatTensor)
y_train = torch.cat((y0, y1), 0).type(torch.FloatTensor)
#测试集
x0_test = torch.normal(1*torch.ones(3000,200),1)
y0_test = torch.zeros(3000)
x1_test = torch.normal(-1*torch.ones(3000,200),1)
y1_test = torch.ones(3000)
x_test = torch.cat((x0_test, x1_test), 0)
y_test = torch.cat((y0_test, y1_test), 0)
定义data_iter函数读取数据:
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)])
yield features.index_select(0, j), labels.index_select(0, j)
模型参数定义初始化、激活函数、模型定义、随机梯度下降函数均与回归问题相同,损失函数调用nn.BCEloss函数:
#损失函数
loss = torch.nn.BCELoss()
训练函数中不同的是每一轮的loss值计算部分:
y_hat = net(X)
l = loss(torch.sigmoid(y_hat), y.view(-1, 1)).sum()
(3).多分类问题
Minist数据集下载和读取:
mnist_train=torchvision.datasets.MNIST(root='~/Datasets/MNIST', train=True,
download=True, transform=transforms.ToTensor())
mnist_test=torchvision.datasets.MNIST(root='~/Datasets/MNIST', train=False,
transform=transforms.ToTensor())
batch_size = 32
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False)
根据数据集设置num_inputs、num_outputs为784和10,与二分类问题相比,不同的是损失函数,调用nn.CrossEntropyLoss函数:
#交叉熵损失函数
loss=torch.nn.CrossEntropyLoss()
并修改训练函数中loss值计算部分:
y_hat = net(X)
l = loss(y_hat, y).sum()
多分类问题中还加入了训练集和测试集准确率的计算,准确率函数计算定义:
def evaluate_accuracy(data_iter, net,loss):
acc_sum, n = 0.0, 0
test_l_sum=0.0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
l=loss(net(X),y).sum()
test_l_sum += l.item()
n += y.shape[0]
return acc_sum / n,test_l_sum/n
4.2 利用torch.nn实现前馈神经网络解决上述回归、二分类、多分类问题
(1)回归问题
生成数据集和读取数据集方式与手动实现相同,接下来实现FlattenLayer层:
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer,self).__init__()
def forward(self,x):
return x.view(x.shape[0],-1)
模型定义和参数初始化:
num_outputs = 1
num_hiddens = 256
net=nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
)
for params in net.parameters():
init.normal_(params,mean=0,std=0.01)
损失函数、sgd函数部分与手动实现相同,依次设置训练轮次、学习率和优化器:
lr=0.001
optimizer= torch.optim.SGD(net.parameters(),lr)
loss = squared_loss
训练函数部分与之前的相同,但是torch.nn实现需要设置优化器optimizer,手动实现时optimizer设置为none。
(2)二分类问题
生成与读取数据集与手动实现时方式相同,然后再实现FlattenLayer层、定义模型以及参数初始化:
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer,self).__init__()
def forward(self,x):
return x.view(x.shape[0],-1)
num_inputs = 200
num_outputs = 1
num_hiddens = 128
net=nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
)
for params in net.parameters():
init.normal_(params,mean=0,std=0.01)
损失函数、sgd函数部分与手动实现相同,不同的是需要设置优化器:
#优化器
optimizer= torch.optim.SGD(net.parameters(),lr)
训练函数部分与之前的相同。
(3)多分类问题
采用与手动实现同样的方法,先实现minist数据集的下载和读取,接着利用torch.nn实现FlattenLayer层、定义模型以及参数初始化,再定义sgd函数、准确率计算函数、设置优化器,而损失函数调用nn.CrossEntropyLoss,最后编写训练函数,输出结果。
#损失函数
loss=torch.nn.CrossEntropyLoss()
4.3 在多分类实验的基础上使用至少三种不同的激活函数
在利用torch.nn实现前馈神经网络的多分类问题的代码基础上,除了原有的relu激活函数,再增加sigmoid和leakyrelu函数,实现三种模型定义,其中,net1、net2、net3分别为使用relu函数、sigmoid和leakyrelu函数的三种模型:
(1)
#Relu激活函数
net1 = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net1.parameters():
init.normal_(params,mean=0,std=0.01)
optimizer1 = optim.SGD(net1.parameters(), lr=lr)
(2)
#Sigmoid激活函数
net2 = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.LogSigmoid(),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net2.parameters():
init.normal_(params,mean=0,std=0.01)
optimizer2 = optim.SGD(net2.parameters(), lr=lr)
(3)
#LeakyReLU激活函数
net3 = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.LeakyReLU(0.1),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net3.parameters():
init.normal_(params,mean=0,std=0.01)
optimizer3 = optim.SGD(net3.parameters(), lr=lr)
训练过程、损失函数不变,为了更好的对比,输出结果包括每一轮训练集和测试集的loss值与准确率,并分别打印四个曲线图进行对比。先分别初始化图表的参数并进行训练:
x_axis , y_train_loss, y_test_loss, y_train_acc, y_test_acc = [],[],[],[],[]
print('激活函数为relu:')
train(net1,train_iter,test_iter,loss,num_epochs,batch_size,params,lr,optimizer1)
y_train_loss_Relu, y_test_loss_Relu, y_train_acc_Relu, y_test_acc_Relu = y_train_loss, y_test_loss, y_train_acc, y_test_acc
x_axis , y_train_loss, y_test_loss, y_train_acc, y_test_acc = [],[],[],[],[]
print('激活函数为sigmoid:')
train(net2,train_iter,test_iter,loss,num_epochs,batch_size,params,lr,optimizer2)
y_train_loss_Sig, y_test_loss_Sig, y_train_acc_Sig, y_test_acc_Sig = y_train_loss, y_test_loss, y_train_acc, y_test_acc
x_axis , y_train_loss, y_test_loss, y_train_acc, y_test_acc = [],[],[],[],[]
print('激活函数为leakyrelu:')
train(net3,train_iter,test_iter,loss,num_epochs,batch_size,params,lr,optimizer3)
y_train_loss_LeakyReLU, y_test_loss_LeakyReLU, y_train_acc_LeakyReLU, y_test_acc_LeakyReLU = y_train_loss, y_test_loss, y_train_acc, y_test_acc
然后定义打印曲线的函数painting(),下边只展示一个曲线图的代码,其余三个修改参数名称即可:
def painting():
plt.figure(1, figsize=(8, 6))
plt.xlabel("epoch")
plt.ylabel("loss")
plt.title("Train Loss")
plt.figure(2, figsize=(8, 6))
plt.figure(1)
p1_1 = plt.plot(x_axis, y_train_loss_Relu, 'b-', label=u'Relu')
plt.legend()
p2_1 = plt.plot(x_axis, y_train_loss_Sig, 'r-', label=u'Sigmoid')
plt.legend()
p3_1 = plt.plot(x_axis, y_train_loss_LeakyReLU, 'y-', label=u'LeakyReLU')
plt.legend()
4.4 对多分类任务中的模型评估隐藏层层数和隐藏单元个数对实验结果的影响
(1)隐藏层层数
在实现多分类问题的代码基础上修改,设置隐藏层层数分别为1、2、3层的网络模型,并设置相应的优化器:
#1层隐藏层
net_1layer = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net_1layer.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_1layer = optim.SGD(net_1layer.parameters(), lr=lr)
#2层隐藏层
net_2layer = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net_2layer.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_2layer = optim.SGD(net_2layer.parameters(), lr=lr)
#3层隐藏层
net_3layer = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs),
).cuda()
for params in net_3layer.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_3layer = optim.SGD(net_3layer.parameters(), lr=lr)
分别输出4个曲线图,与上一个实验输出代码基本相同,修改相应的参数即可。
(2)隐藏单元个数
在实现多分类问题的代码基础上修改,设置隐藏单元个数分别为64、128、512的网络模型,并设置相应的优化器:
#64单元
net_64point = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens_64),
nn.ReLU(),
nn.Linear(num_hiddens_64,num_outputs),
).cuda()
for params in net_64point.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_64 = optim.SGD(net_64point.parameters(), lr=lr)
#128单元
net_128point = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens_128),
nn.ReLU(),
nn.Linear(num_hiddens_128,num_outputs),
).cuda()
for params in net_128point.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_128 = optim.SGD(net_128point.parameters(), lr=lr)
#512单元
net_512point = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens_512),
nn.ReLU(),
nn.Linear(num_hiddens_512,num_outputs),
).cuda()
for params in net_512point.parameters():
init.normal_(params,mean=0,std=0.01)
#优化器
optimizer_512 = optim.SGD(net_512point.parameters(), lr=lr)
分别输出4个曲线图,与上一个实验输出代码基本相同,修改相应的参数即可。
4.5 在多分类任务实验中实现momentum、rmsprop、adam优化器
# 准备数据和模型
input_data = torch.randn(100, 10) # 100个样本,每个样本10维输入
labels = torch.randint(0, 3, (100,)) # 100个样本的标签,3类分类
model = Classifier()
# 定义优化器
momentum_optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
rmsprop_optimizer = optim.RMSprop(model.parameters(), lr=0.001, alpha=0.9)
adam_optimizer = optim.Adam(model.parameters(), lr=0.001)
# 定义损失函数
criterion = nn.CrossEntropyLoss()
# 训练过程
for epoch in range(10):
momentum_optimizer.zero_grad()
rmsprop_optimizer.zero_grad()
adam_optimizer.zero_grad()
output = model(input_data)
loss = criterion(output, labels)
# 使用不同的优化器进行反向传播和参数更新
loss.backward()
momentum_optimizer.step()
rmsprop_optimizer.step()
adam_optimizer.step()
4.6 在多分类任务实验中分别手动实现和用torch.nn实现L_2正则化
1.手动实现
在实现多分类问题的代码基础上修改,添加L2范数惩罚项:
def l2_penalty(W1,W2):
w=((W1**2).sum()+(W2**2).sum())/2
return w
再修改训练函数,添加lambd参数来表示权重,并修改loss值的计算:
y_hat = net(X)
l = loss(y_hat, y) + lambd * l2_penalty(W1, W2)
最后输出W1和W2对应的参数L2范数:
print('L2 norm of W1:', W1.norm().item())
print('L2 norm of W2:', W2.norm().item())
2.用torch.nn实现
在实现多分类问题的代码基础上修改,只需修改优化器设置:
#优化器
optimizer=optim.SGD(net.parameters(),lr=lr,weight_decay=0.01)
4.7在多分类任务实验中分别手动实现和用torch.nn实现dropout
1.手动实现
在实现多分类问题的代码基础上修改,添加dropout的网络模型定义,隐藏层丢弃率设为0.3:
drop_prob=0.5
def net(X,is_training=True):
X=X.view((-1,num_inputs))
H = relu(torch.matmul(X, W1.t()) + b1)
if is_training:
H=dropout(H,drop_prob)
return torch.matmul(H,W2.t())+b2
修改计算准确率的函数定义,设置为测试时不适用dropout:
def evaluate_accuracy(data_iter, net,loss):
acc_sum, n = 0.0, 0
test_l_sum=0.0
for X, y in data_iter:
acc_sum += (net(X,is_training=False).argmax(dim=1) == y).float().sum().item()
l=loss(net(X),y).sum()
test_l_sum += l.item()
n += y.shape[0]
return acc_sum / n,test_l_sum/n
其余部分与之前相同。
2.用torch.nn实现
在实现多分类问题的代码基础上修改,添加dropout的网络模型定义,隐藏层丢弃率设为0.5:
net=nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Dropout(drop_prob),
nn.Linear(num_hiddens,num_outputs),
)
drop_prob=0.5
修改计算准确率的函数定义,用eval( )和train( )来切换模型的状态:
def evaluate_accuracy(data_iter, net,loss):
acc_sum, n = 0.0, 0
test_l_sum=0.0
for X, y in data_iter:
if isinstance(net,torch.nn.Module):
net.eval()
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
net.train()
l=loss(net(X),y).sum()
test_l_sum += l.item()
n += y.shape[0]
return acc_sum / n,test_l_sum/n
其余部分与之前相同。
4.8 对多分类任务实验中实现早停机制,并在测试集上测试
# 创建早停对象,这里设置早停的指标是误差的改变,最大迭代次数为5,容忍度为0.001
es = EarlyStopping(monitor='error_change', patience=5, min_delta=0.001)
# 在fit方法中加入早停对象
clf.fit(X_train, y_train, early_stopping=es)
其余部分与之前相同。
五、实验结果
实验结果包括程序运行结果以及对结果的分析,尽量用图表展示实验结果,并且通过结果进行相关的分析。
5.1 手动实现前馈神经网络解决上述回归、二分类、多分类问题
1.回归问题
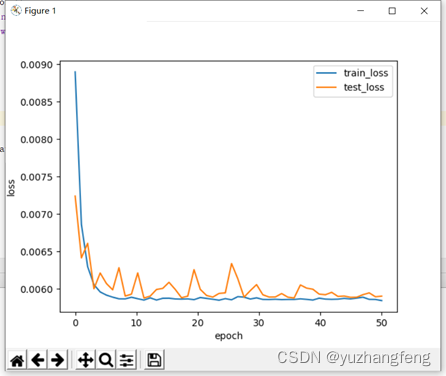
图1 loss曲线图
2.二分类问题
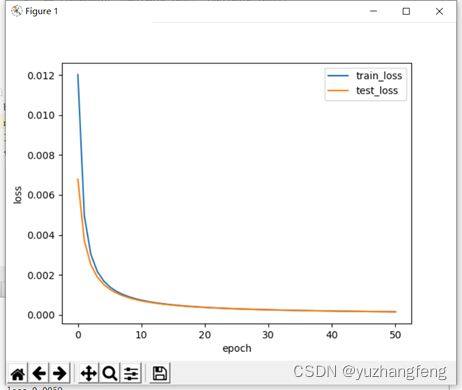
图2 loss曲线图
3.多分类问题
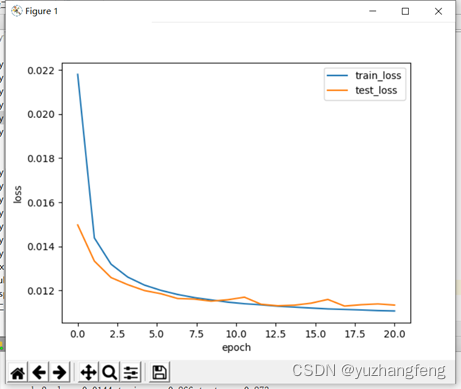
图3 loss曲线图
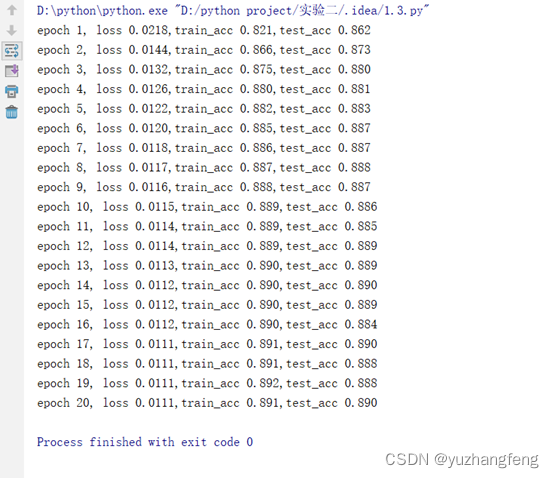
图4 每一轮输出结果
5.2 利用torch.nn实现前馈神经网络解决上述回归、二分类、多分类问题
1.回归问题
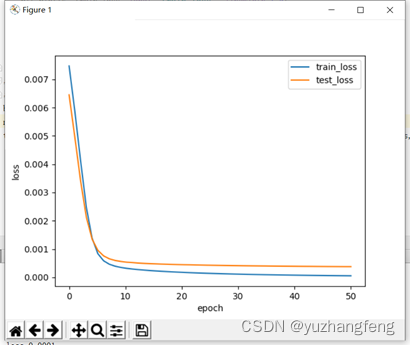
图5 loss曲线图
2.二分类问题
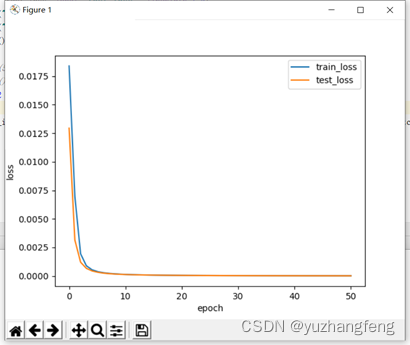
图6 loss曲线图
3.多分类问题
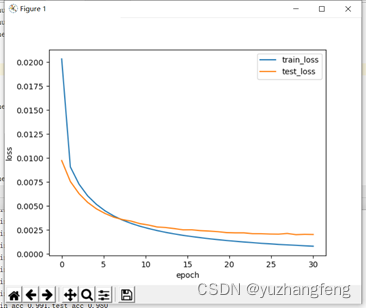
图7 loss曲线图
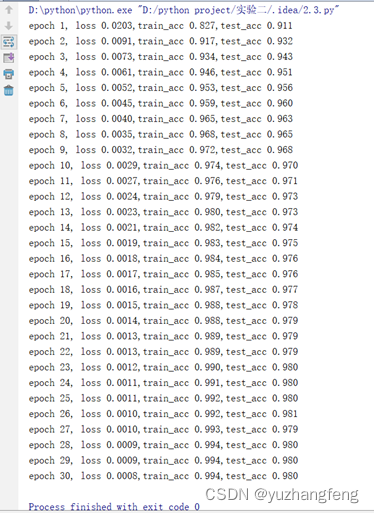
图8 每一轮输出结果
5.3 在多分类实验的基础上使用至少三种不同的激活函数
(1)由下图可以看出,使用sigmoid函数得出的train loss值明显高于其他两个,使用relu和leakyrelu得出的train loss值基本相同,曲线接近重合。
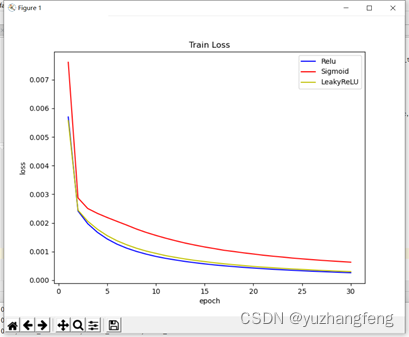
图9 三种激活函数对应train loss值
(2)由下图可以看出,使用sigmoid函数得出的test loss值明显高于其他两个,使用leakyrelu得出的train loss值略高于使用relu时。
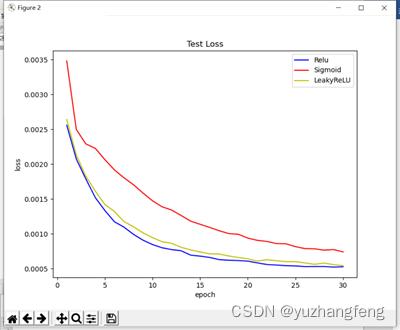
图10 三种激活函数对应test loss值
(3)由下图可以看出,使用sigmoid函数得出的train acc值明显低于其他两个,使用leakyrelu和使用relu时曲线基本重合。
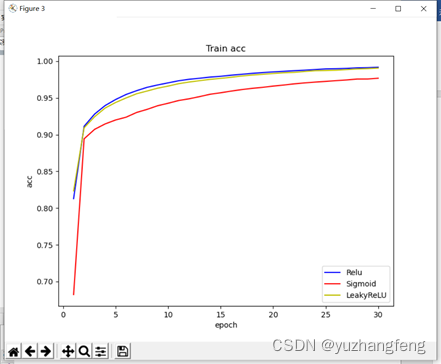
图11 三种激活函数对应train acc值
(4)由下图可以看出,使用sigmoid函数得出的test acc值明显低于其他两个,使用leakyrelu得出的test acc值略低于使用relu时。

图12 三种激活函数对应test acc值
激活函数为relu:

图13 relu函数对应每一轮输出结果
激活函数为sigmoid:

图14 sigmoid函数对应每一轮输出结果
激活函数为leakyrelu:

图15 leakyrelu函数对应每一轮输出结果
结合上述实验结果,可以看出,在解决回归问题时,使用sigmoid激活函数结果不是那么理想,使用relu和leakyrelu结果较好,而relu略好于leakyrelu。
5.4对多分类任务中的模型评估隐藏层层数和隐藏单元个数对实验结果的影响
(1)隐藏层层数分别为1、2、3时:
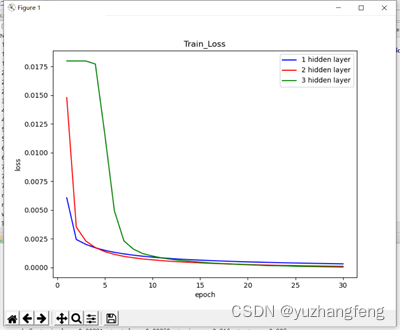
图16 不同隐藏层层数对应train loss值
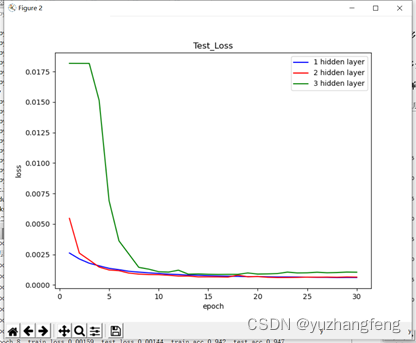
图17 不同隐藏层层数对应test loss值
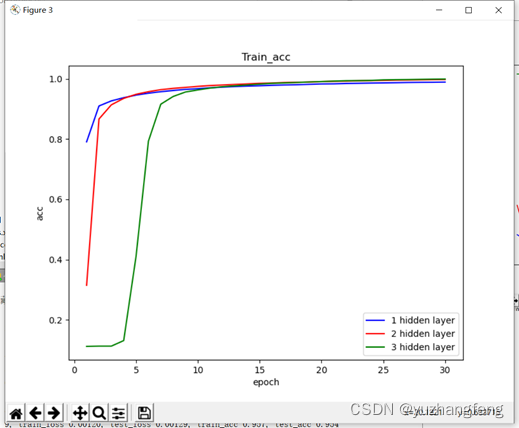
图18 不同隐藏层层数对应train acc值
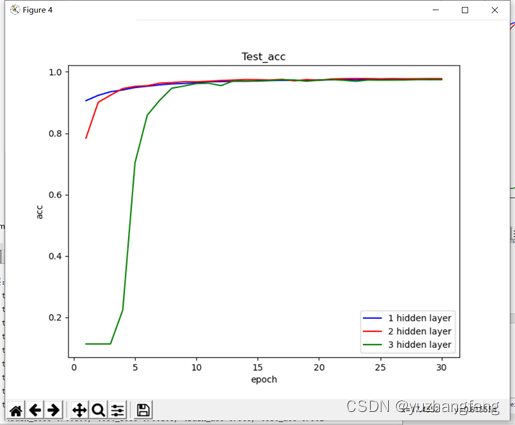
图19 不同隐藏层层数对应test acc值

图20 1层隐藏层对应每一轮输出结果
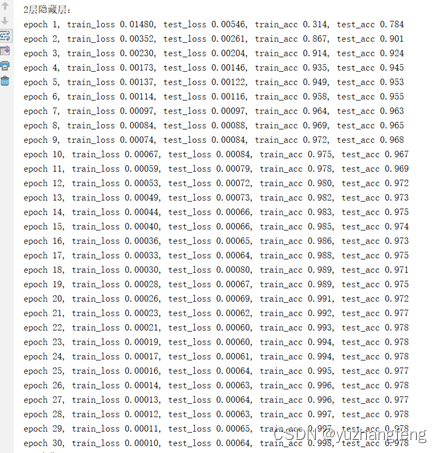
图21 2层隐藏层对应每一轮输出结果

图22 3层隐藏层对应每一轮输出结果
结合上述实验结果可以看出,在解决多分类问题中,开始时隐藏层层数越高,训练集和测试集的loss值都是越高,准确率越低,而到了后边,曲线基本相同。
(2)隐藏单元个数分别为64、128、512时:
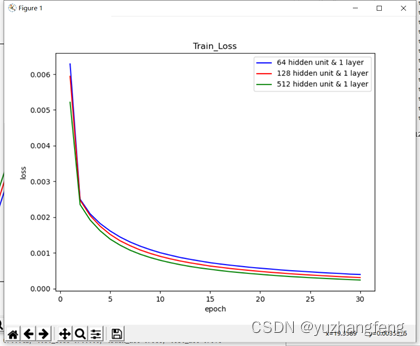
图23 不同隐藏单元个数对应train loss值
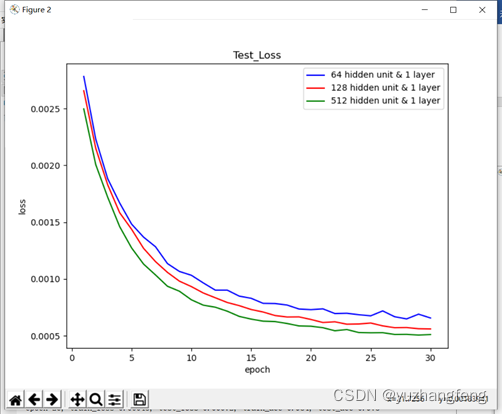
图24 不同隐藏单元个数对应test loss值
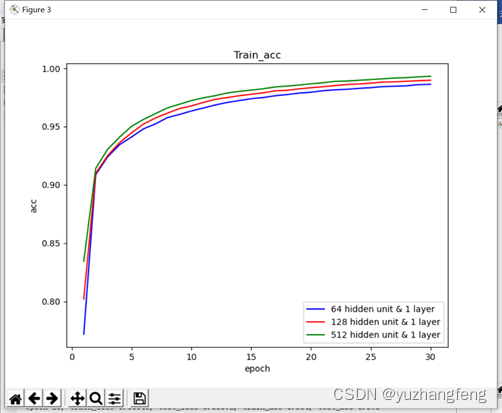
图25 不同隐藏单元个数对应train acc值
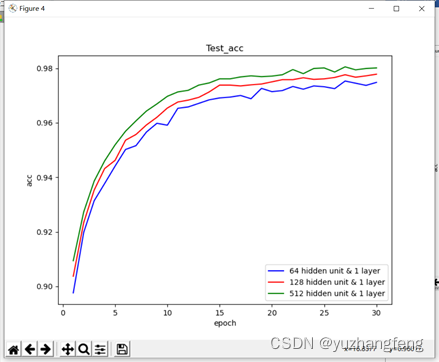
图26 不同隐藏单元个数对应test acc值

图27 64个单元对应每一轮输出结果

图28 128个单元对应每一轮输出结果

图29 512个单元对应每一轮输出结果
结合上述实验结果可以看出,隐藏单元个数越多,所得到的训练集和测试集的loss值越低,准确率越高。
5.5 在多分类任务实验中实现momentum、rmsprop、adam优化器
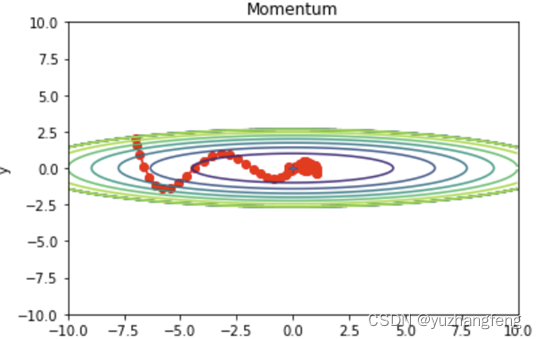
图30 momentum效果
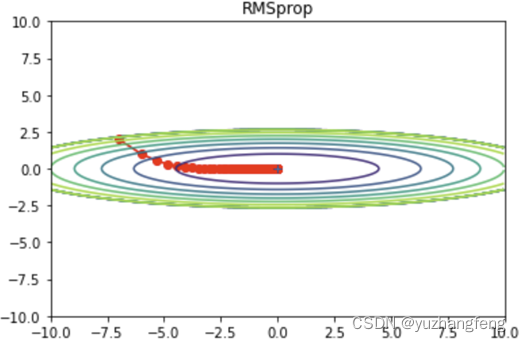
图31 rmsprop效果
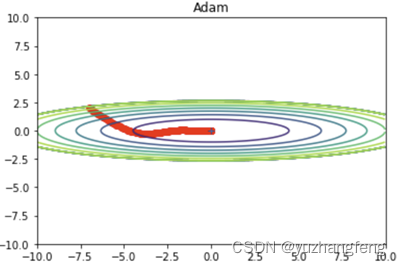
图32 Adam效果
由此可以得出,Momentum可以加速在某些方向上的更新,抑制在某些方向上的震荡,对于具有非单调、具有较多局部最小值或者优化路径曲率变化较大的问题,Momentum表现较好。但Momentum可能会在"死区"附近震荡,导致无法找到最小值。RMSProp可以自适应地调整学习率,对于具有非单调、具有较多局部最小值或者优化路径曲率变化较大的问题,RMSProp表现较好。但RMSProp对β的选择很敏感,不同的β可能会产生非常不同的结果。Adam在大多数任务中都表现优秀,它结合了Momentum和RMSProp的优点,对于非凸、非单调、具有较多局部最小值或者优化路径曲率变化较大的问题,Adam表现较好。
5.6在多分类任务实验中分别手动实现和用torch.nn实现L_2正则化
(1)手动实现
A.lambd=0(即不使用正则化)
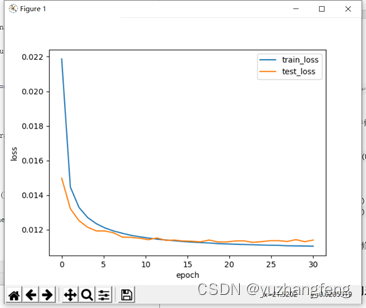
图33 loss曲线图
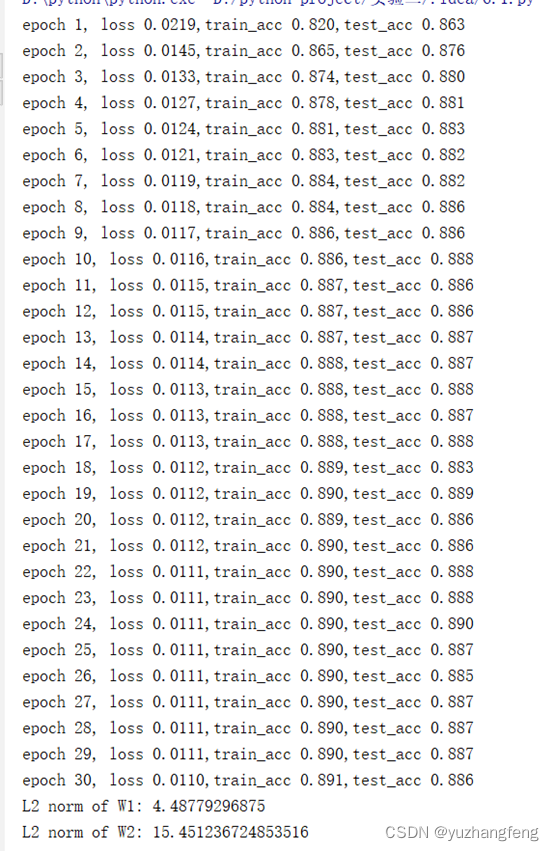
图34 每一轮输出结果
B.lambd=0.01
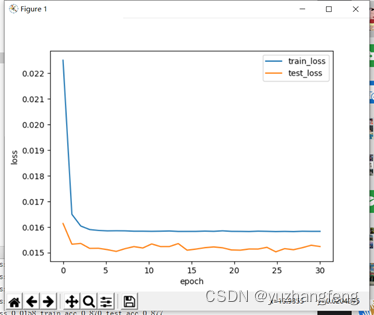
图35 loss曲线图
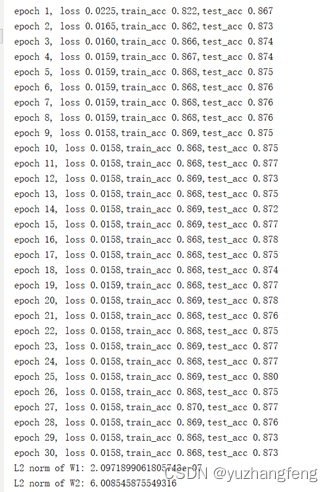
图36 每一轮输出结果
可以看到,使用正则化后,参数L2范数变小,参数更接近0。
(2)用torch.nn实现
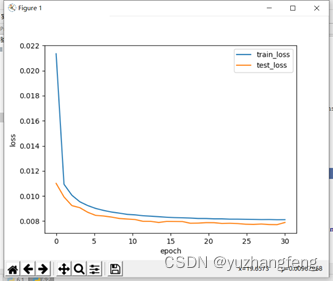
图37 loss曲线图
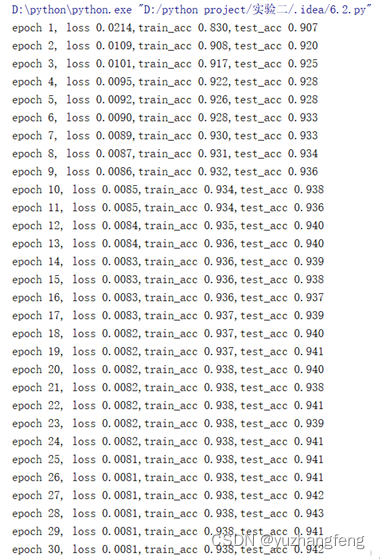
图38 每一轮输出结果
5.7 在多分类任务实验中分别手动实现和用torch.nn实现dropout
(1)手动实现
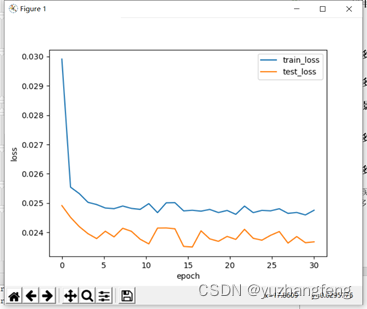
图39 loss曲线图
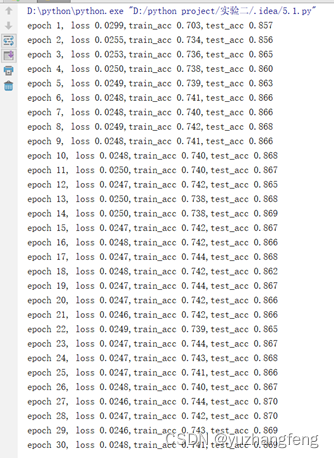
图40 每一轮输出结果
(2)用torch.nn实现
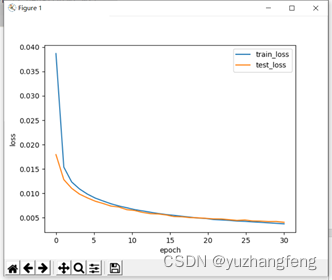
图41 loss曲线图
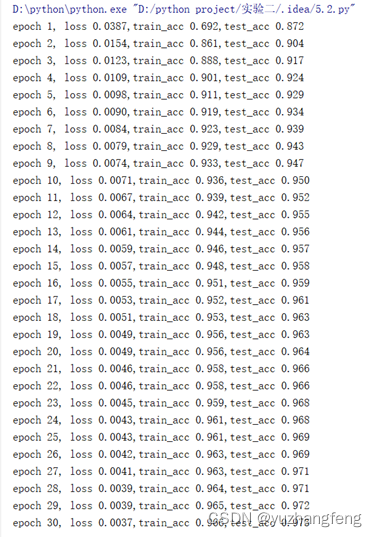
图42 每一轮输出结果
结合上述实验结果可以看出,手动实现且是在训练时使用dropout时,训练集的准确率明显低于测试集许多,而用torch.nn实现则相差不大,训练集准确率只是略低于测试集准确率。
六、实验心得体会
通过这次实验,我学习了如何处理数据、构建网络结构和选择合适的激活函数。我了解到前馈神经网络的特点,例如其信息的单向流动性和层与层之间的独立性。通过调整网络参数,如学习率、迭代次数和隐藏层数量,我观察到了网络性能的变化,并理解了如何优化这些参数。
在实验过程中,我也遇到了许多挑战。例如,对多分类任务实现L2正则化时,权重lambd需要选一个接近0的数才能得到较好的结果,因为与课件上使用的数据集不同,参考课件上所给的lambd=3,会得到很不理想的实验结果。同时在实验中,我发现我对概念和一些公式的理解不到位,比如在实现L2正则化时,因为有两个W,查了许多博客才理解要输出的新W该怎么表示等等。
这次实验使我受益匪浅,我深刻认识到神经网络的应用前景广阔。前馈神经网络可用于解决分类和回归问题,且具有强大的表征学习能力。在实际应用中,我们可以根据不同的任务需求调整网络结构,例如添加更多的隐藏层或使用不同的激活函数。希望下一次实验能做得更好。