LeetCode 1503. 所有蚂蚁掉下来前的最后一刻【脑筋急转弯】1618

news2024/9/26 3:26:09

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

有一块木板，长度为 n 个单位。一些蚂蚁在木板上移动，每只蚂蚁都以 每秒一个单位 的速度移动。其中，一部分蚂蚁向左移动，其他蚂蚁向右移动。

当两只向不同方向移动的蚂蚁在某个点相遇时，它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。

而当蚂蚁在某一时刻 t 到达木板的一端时，它立即从木板上掉下来。

给你一个整数 n 和两个整数数组 left 以及 right 。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0 时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。

示例 1：

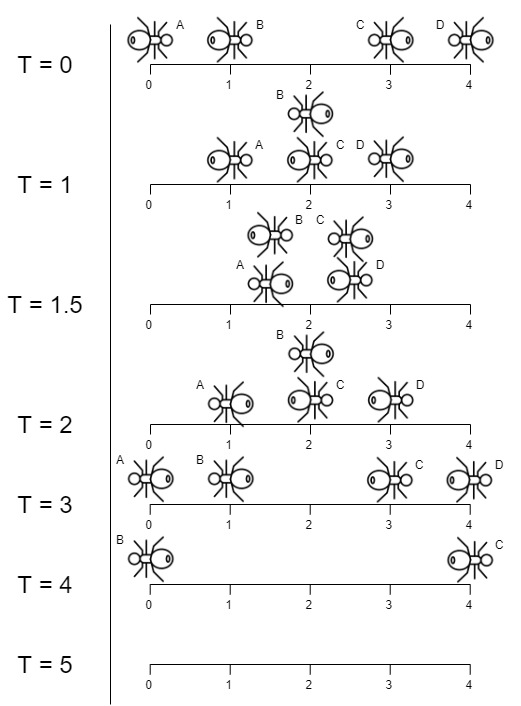
输入：n = 4, left = [4,3], right = [0,1]
输出：4
解释：如上图所示：
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意，蚂蚁在木板上的最后时刻是 t = 4 秒，之后蚂蚁立即从木板上掉下来。（也就是说在 t = 4.0000000001 时，木板上没有蚂蚁）。

示例 2：

输入：n = 7, left = [], right = [0,1,2,3,4,5,6,7]
输出：7
解释：所有蚂蚁都向右移动，下标为 0 的蚂蚁需要 7 秒才能从木板上掉落。

示例 3：

输入：n = 7, left = [0,1,2,3,4,5,6,7], right = []
输出：7
解释：所有蚂蚁都向左移动，下标为 7 的蚂蚁需要 7 秒才能从木板上掉落。

提示：

1 <= n <= 10^4
0 <= left.length <= n + 1
0 <= left[i] <= n
0 <= right.length <= n + 1
0 <= right[i] <= n
1 <= left.length + right.length <= n + 1
left 和 right 中的所有值都是唯一的，并且每个值 只能出现在二者之一 中。

解法脑筋急转弯

本题是2731. 移动机器人的前置。

当一只蚂蚁起始位置为 $x$ ，方向往左，且往左移动过程不受其他影响时，其到达左边界所需时间为 $x$ ；若方向往右，且往右移动过程不受其他影响时，其到达右边界所需时间为 $n - x$ 。

蚂蚁之间的相遇，实际上并不会影响它们到达木板边缘的时间。两只相遇的蚂蚁只是简单地交换了彼此的移动方向，并没有影响到它们的移动步数，即两只蚂蚁相遇可视为身份互换。

因此，我们只需要分别计算每只蚂蚁单独掉落到木板边缘所需的时间，然后取最大值即可得到所有蚂蚁掉落的最后时刻。

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        return max(n - 
            (right.empty() ? n : *min_element(right.begin(), right.end())),
            left.empty() ? 0 : *max_element(left.begin(), left.end())
        );
    }
};