1、傅里叶变换（FT）

傅里叶变换（连续时间傅里叶变换）是该部分内容的理论基础，回顾一下：

傅里叶变换：

        

傅里叶逆变换：

        

以上是连续时间傅里叶变换，但计算机只能处理离散的数据。因此有了离散傅里叶变换（DFT），下面进行详细推导。

---

2、离散傅里叶变换（DFT）

2.1 采样和离散时间傅里叶变换（DTFT）

使用采样可将连续域上的数据离散化。信号学科里面使用冲激序列串来对连续信号采样。

有信号，现对其采样。若采样频率为 ，则采样间隔  ，用以采样的冲激序列串定义为：

        

因此采样后的信号为：

        

此时将采样后信号  代入傅里叶变换公式：

        

交换积分与求和次序：

        

由  函数的筛选性 ，将上式中  看成， 得到离散时间傅里叶变换（DTFT）：

        

因为  表示采样的时间点，所以可令 ，因此离散时间傅里叶变换的更一般形式为：

        

---

2.2 离散傅里叶变换（DFT）

2.1中通过采样使得信号在时域离散化，但并不能保证其频域也离散化，同样不利于计算机处理。

由性质：时域离散，频域周期化；频域离散，时域周期化。因此若想让信号在频域也离散，则需要该信号在时域上为周期信号。

但原信号不一定为周期信号。解决方式是周期延拓：截取原无限长信号的个采样点，假设：

① 个采样点为原信号的一个周期；

  

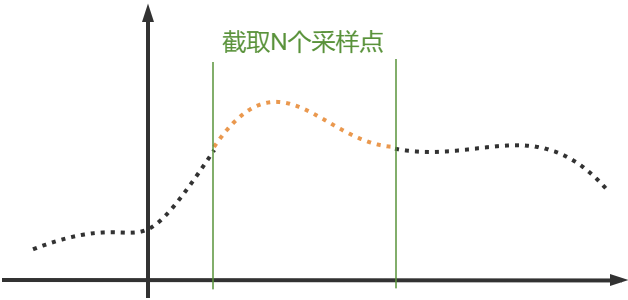
② N个采样点外为该N点的周期延拓。

 

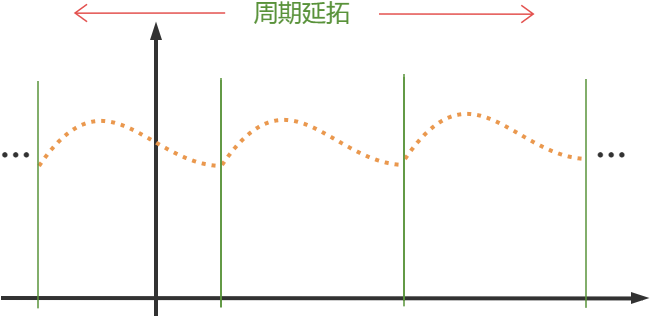
这样原先的离散非周期信号就变成离散周期信号，因此频域得以离散化。

在上述周期延拓的基础上，假设采样间隔为  ，则个采样点的采样周期 ，从连续信号中截取的个采样点的信号可表示为：

        

因为周期延拓，为是周期信号，周期函数的傅里叶级数为：​ 

         

将代入其中，得：

        

交换积分与求和次序：

        

同理，由  函数的筛选性，上式变为：

        

因为，，代入上式：

        

令，，得离散傅里叶变换（DFT）的表达式为：

        ，   且 

离散傅里叶逆变换（IDFT）的表达式为：

        

注意：为了满足正逆变换的自洽，放在正逆变换其中之一前就可以，通常放在逆变换前。

补充：令，则：

        

---

2.3 离散傅里叶变换（DFT）的C语言实现

根据上述推导出的公式，很容易编码实现。如下：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define PI 3.1415927

double realComput(double xn[], int ndft, int k);
double imageComput(double xn[], int ndft, int k);

typedef struct {
	double real;
	double image;
} Complex;

void dft(double x[], int ndft) {
	Complex* dftRes = (Complex*)malloc(ndft * sizeof(Complex));
	if (dftRes == NULL) {
		return;
	}

	for (int i = 0; i < ndft; ++i) {
		dftRes[i].real = realComput(x, ndft, i);
		dftRes[i].image = imageComput(x, ndft, i);
		printf("%lf + %lfi\n", dftRes[i].real, dftRes[i].image);
	}

	free(dftRes);
}

double realComput(double xn[], int ndft, int k) {
	double realPart = 0;
	for (int i = 0; i < ndft; ++i) {
		realPart += xn[i] * cos(2 * PI / ndft * k * i);
	}
	return realPart;
}

double imageComput(double xn[], int ndft, int k) {
	double imagePart = 0;
	for (int i = 0; i < ndft; ++i) {
		imagePart -= xn[i] * sin(2 * PI / ndft * k * i);
	}
	return imagePart;
}

int main() {
	double xn[9] = {1,2,3,4,5,0,0,0,85};
	dft(xn, sizeof(xn) / sizeof(double));
	system("pause");
	return 0;
}

运行结果：

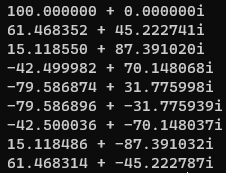
暂未发现问题。