1. 启用适用于 Linux 的 Windows 子系统和虚拟机功能
以管理员身份打开 PowerShell(“开始”菜单 >“PowerShell” >单击右键 >“以管理员身份运行”),然后依次输入执行以下命令:
dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestartdism.exe /online /enable-feature /featurename:VirtualMachinePlatform /all /norestart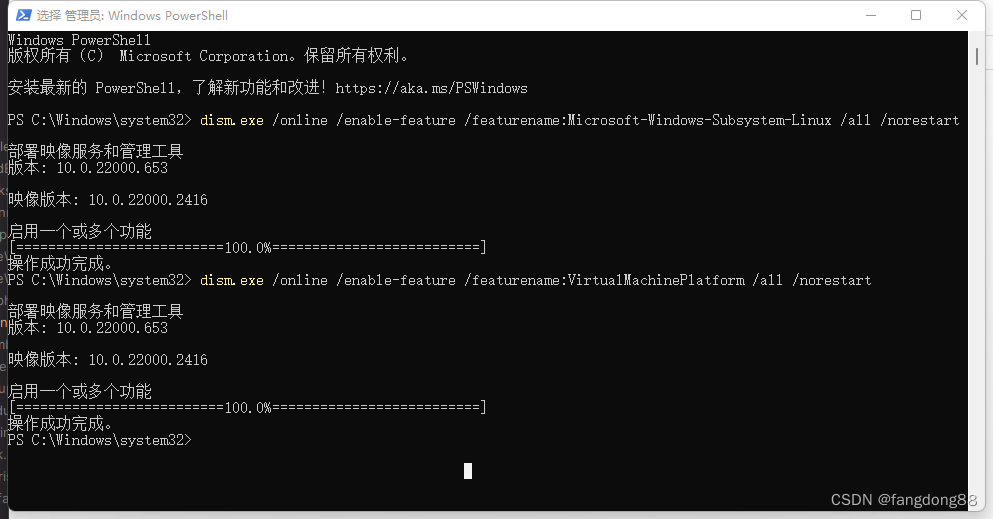
执行完后记得一定要重启!!!!
2.下载WSL Linux 发行版
打开官方网址 https://learn.microsoft.com/zh-cn/windows/wsl/install-manual#step-4---download-the-linux-kernel-update-package
找到最下方下载发行版处

这里可选择需要下载安装的版本
这里选择以 Ubuntu 20.04 为例
下载完后将文件后缀改为 .zip
解压找到 Ubuntu_2004.2021.825.0_x64.appx,将其后缀改为 .zip
然后将该压缩包放到需要安装的目录解压

解压完成后运行子系统 ubuntu.exe

如果运行有报错提示 Error: 0x800701bc WSL 2 ?????????????????? https://aka.ms/wsl2kernel
需要打开命令终端,执行以下命令:
wsl --update
wsl --shutdown再次运行 ubuntu.exe 即可
正常情况下会提示安装并要求输入新的用户名密码等,接下来就可以愉快的使用了~
官方链接:适用于 Linux 的 Windows 子系统文档 | Microsoft Learn







![[架构之路-235]:目标系统 - 纵向分层 - 数据库 - 数据库系统基础与概述:数据库定义、核心概念、系统组成](https://img-blog.csdnimg.cn/76a0d6187de341e6b14c43dc6d72e1d4.png)