一、简介
在本文中,我们重点关注一些小众但值得注意的移动平均方法。这些利基工具通常来自专门研究或开发用于解决非常特殊的交易场景。虽然不太主流,但它们提供了对市场动态的极其细致入微的见解。完整列表如下:
- 第 1 部分 — 基本技术:简单移动平均线 (SMA)、指数移动平均线 (EMA)、加权移动平均线 (WMA)、双指数移动平均线 (DEMA)、三重指数移动平均线 (TEMA)、交易量调整移动平均线 (VAMA) 、自适应移动平均线(AMA 或 KAMA)、三角移动平均线(TMA)、赫尔移动平均线(HMA)
- 第 2 部分 — 自适应和动态:分形自适应移动平均线 (FRAMA)、零滞后指数移动平均线 (ZLEMA)、可变指数动态平均线 (VIDYA)、Arnaud Legoux 移动平均线 (ALMA)、MESA 自适应移动平均线 (MAMA)、跟随自适应移动平均线 (FAMA)、自适应周期移动平均线、彩虹移动平均线、Wilders 移动平均线、平滑移动平均线 (SMMA)
- 第 3 部分 — 高级加权:顾比多重移动平均线 (GMMA)、最小二乘移动平均线 (LSMA)、韦尔奇移动平均线或修正移动平均线、正弦加权移动平均线、中位数移动平均线、几何移动平均线、弹性成交量加权移动平均线 ( eVWMA)、正则指数移动平均线 (REMA)、抛物线加权移动平均线
- 第 4 部分—从利基市场到值得注意:Jurik 移动平均线 (JMA)、端点移动平均线 (EPMA)、Chande 移动平均线 (CMA)、谐波移动平均线、McGinley 动态、锚定移动平均线、Holt-Winters 移动平均线、过滤移动平均线, Kijun Sen(基线)
2.背景和Python实现
本节从理论和实践的角度探讨了这些方法。最终目标是提供一个基于 Python 的实现,让它们全部发挥作用。
2.1 尤里克移动平均线(JMA)
Jurik 移动平均线 (JMA) 由 Mark Jurik 开发。它因其流畅性和低延迟而受到赞誉,使其成为交易者的最爱。JMA 旨在通过提供密切跟踪价格走势的平滑曲线来实现两全其美。JMA 尤为独特,因为它会根据波动性和价格走势进行实时调整。
JMA 的精确公式和计算方法是专有的。然而,有一些可用的近似值,并且许多平台都提供 JMA 作为内置函数。出于我们的目的,并为了避免任何专有问题,我不会提供确切的公式,但会提供基于可用近似值和现有库的 Python 实现。
虽然许多移动平均线要求交易者在响应性和平滑性之间做出妥协,但 JMA 巧妙地规避了这一困境。它的适应性确保它与当前的价格走势保持密切联系,提供减少滞后的见解。
# Required Libraries
import yfinance as yf
import matplotlib.pyplot as plt
from pandas import Series
from numpy import average as npAverage
from numpy import nan as npNaN
from numpy import log as npLog
from numpy import power as npPower
from numpy import sqrt as npSqrt
from numpy import zeros_like as npZeroslike
from pandas_ta.utils import get_offset, verify_series
def jma(close, length=None, phase=None, offset=None, **kwargs):
# Validate Arguments
_length = int(length) if length and length > 0 else 7
phase = float(phase) if phase and phase != 0 else 0
close = verify_series(close, _length)
offset = get_offset(offset)
if close is None: return
# Define base variables
jma = npZeroslike(close)
volty = npZeroslike(close)
v_sum = npZeroslike(close)
kv = det0 = det1 = ma2 = 0.0
jma[0] = ma1 = uBand = lBand = close[0]
# Static variables
sum_length = 10
length = 0.5 * (_length - 1)
pr = 0.5 if phase < -100 else 2.5 if phase > 100 else 1.5 + phase * 0.01
length1 = max((npLog(npSqrt(length)) / npLog(2.0)) + 2.0, 0)
pow1 = max(length1 - 2.0, 0.5)
length2 = length1 * npSqrt(length)
bet = length2 / (length2 + 1)
beta = 0.45 * (_length - 1) / (0.45 * (_length - 1) + 2.0)
m = close.shape[0]
for i in range(1, m):
price = close[i]
# Price volatility
del1 = price - uBand
del2 = price - lBand
volty[i] = max(abs(del1),abs(del2)) if abs(del1)!=abs(del2) else 0
# Relative price volatility factor
v_sum[i] = v_sum[i - 1] + (volty[i] - volty[max(i - sum_length, 0)]) / sum_length
avg_volty = npAverage(v_sum[max(i - 65, 0):i + 1])
d_volty = 0 if avg_volty ==0 else volty[i] / avg_volty
r_volty = max(1.0, min(npPower(length1, 1 / pow1), d_volty))
# Jurik volatility bands
pow2 = npPower(r_volty, pow1)
kv = npPower(bet, npSqrt(pow2))
uBand = price if (del1 > 0) else price - (kv * del1)
lBand = price if (del2 < 0) else price - (kv * del2)
# Jurik Dynamic Factor
power = npPower(r_volty, pow1)
alpha = npPower(beta, power)
# 1st stage - prelimimary smoothing by adaptive EMA
ma1 = ((1 - alpha) * price) + (alpha * ma1)
# 2nd stage - one more prelimimary smoothing by Kalman filter
det0 = ((price - ma1) * (1 - beta)) + (beta * det0)
ma2 = ma1 + pr * det0
# 3rd stage - final smoothing by unique Jurik adaptive filter
det1 = ((ma2 - jma[i - 1]) * (1 - alpha) * (1 - alpha)) + (alpha * alpha * det1)
jma[i] = jma[i-1] + det1
# Remove initial lookback data and convert to pandas frame
jma[0:_length - 1] = npNaN
jma = Series(jma, index=close.index)
# Offset
if offset != 0:
jma = jma.shift(offset)
# Handle fills
if "fillna" in kwargs:
jma.fillna(kwargs["fillna"], inplace=True)
if "fill_method" in kwargs:
jma.fillna(method=kwargs["fill_method"], inplace=True)
# Name & Category
jma.name = f"JMA_{_length}_{phase}"
jma.category = "overlap"
return jma
# Fetch data
ticker_symbol = "AAPL"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# length
n = 28
# Compute JMA
data['JMA'] = jma(data['Close'], length=n, phase=0)
# Plot
plt.figure(figsize=(20,7))
plt.title(f'{ticker_symbol} Stock Price and JMA (n = {n})', fontsize=16)
plt.plot(data['Close'], label='Stock Price', color='black', alpha=0.6)
plt.plot(data['JMA'], label='JMA', color='green', alpha=0.8)
plt.legend(loc='upper left')
plt.grid(True, alpha=0.3)
plt.xlabel('Date', fontsize=14)
plt.ylabel('Price', fontsize=14)
plt.show()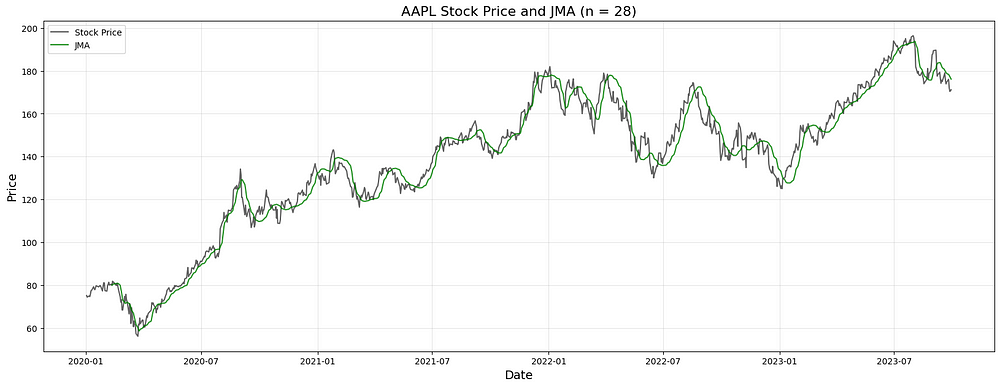
图 1: Apple Inc. (AAPL) 2020 年至 2023 年股价,辅以使用 14 天周期和 0 相位的 Jurik 移动平均线 (JMA)。JMA 以其自适应功能而闻名,可提供高效的平滑价格数据,同时对市场变动做出反应。
2.2 端点移动平均线(EPMA)
端点移动平均线(EPMA)是一种修改后的简单移动平均线,它通过计算数据集的线性回归趋势线并使用该趋势线的端点作为移动平均线,更加强调最新的数据。
其基本原理是,这种方法将更好地捕捉价格序列中的主导趋势,并提供比简单移动平均线更准确的表示。
要计算周期n的 EPMA ,步骤如下:
- 计算过去n 个收盘价的线性回归趋势线。
- 使用回归线的端点作为该期间的 EPMA。
线性回归线的公式为
![]()
方程 2.2.1。线性回归:用于计算一段时间内“n”个收盘价的趋势线,作为终点移动平均线 (EPMA) 的基础。
在哪里:
- m是直线的斜率。
- xt是时间t的 x 坐标(通常表示第一个点为 1,第二个点表示为 2,依此类推)。
- c是 y 轴截距。
终点是当xt = n时,所以
![]()
方程 2.2.2。EPMA:当xt = n时线性回归线的 y 坐标。与传统 SMA 相比,该端点更能集中地体现当前趋势。
EPMA 旨在通过关注趋势的终点,比传统 SMA 更有效地捕捉当前趋势的本质。它强调最新数据,可能比传统 SMA 更有效地捕捉主导市场趋势。
它对趋势终点的关注使其在波动的市场阶段特别有价值,可以将真正的趋势转变与市场噪音区分开来。对于交易者来说,上升趋势的 EPMA 可以预示看涨势头,而下降趋势可能暗示看跌状况。
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
def calculate_EPMA(prices, period):
epma_values = []
for i in range(period - 1, len(prices)):
x = np.arange(period)
y = prices[i-period+1:i+1]
slope, intercept = np.polyfit(x, y, 1)
epma = slope * (period - 1) + intercept
epma_values.append(epma)
return [None]*(period-1) + epma_values # Pad with None for alignment
# Fetching data
ticker_symbol = "DIS"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
close_prices = data['Close'].tolist()
# Calculate EPMA
epma_period = 28
data['EPMA'] = calculate_EPMA(close_prices, epma_period)
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label=f'{ticker_symbol} Price', color='black')
plt.plot(data.index, data['EPMA'], label=f'EPMA {epma_period}', color='green')
plt.title(f'End Point Moving Average of {ticker_symbol} (n = {epma_period})')
plt.legend()
plt.grid()
plt.show()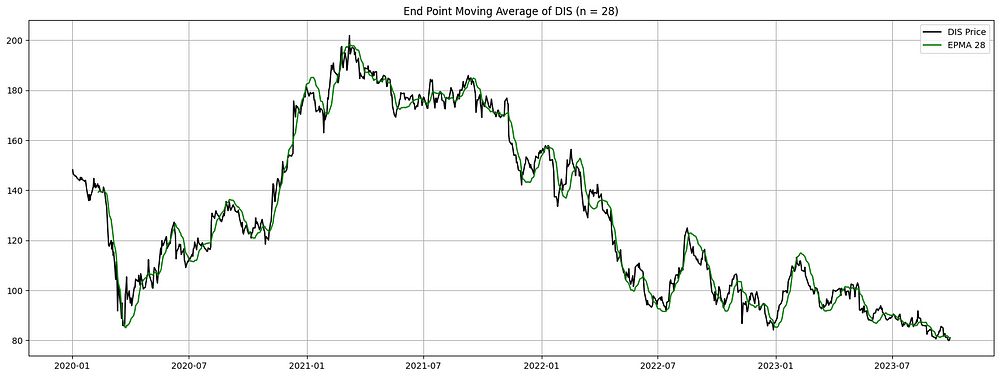
图 2. 2020 年至 2023 年华特迪士尼公司 (DIS) 的端点移动平均线 (EPMA):该图显示 DIS 的股价(黑线)及其 14 天 EPMA(绿线)。EPMA 基于线性回归计算,提供了了解价格趋势的独特方法。
2.3 钱德移动平均线(CMA)
钱德移动平均线 (CMA) 是由 Tushar Chande 开发的一种移动平均线。它与常见的简单移动平均线 (SMA) 不同,因为 SMA 在计算中仅考虑收盘价,而 CMA 则认为该期间内的所有价格都是相等的。钱德移动平均线将累计价格相加,然后除以累计价格数量。
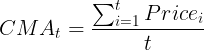
方程 2.3.1。钱德移动平均线 (CMA) 的公式:由 Tushar Chande 提出,CMA 与传统 SMA 的区别在于将其周期内的每个价格视为相等
在哪里:
- CMA_t是时间t的钱德移动平均线。
- Price_i是时间i的价格。
在交易中,钱德移动平均线 (CMA) 为价格变动提供了独特的视角,特别解决了过度依赖收盘价的潜在偏差。通过对同一时期内的每个价格给予同等的权重,CMA 促进了对市场活动的更全面的了解。这种包容性的方法在日内波动较大的市场或当收盘价可能容易受到人为操纵或日终交易异常的影响时尤其有利。
对于交易者来说,使用 CMA 可以更清晰地了解潜在趋势,并减少被不反映更广泛市场情绪的不稳定价格上涨或下跌误导的可能性。从本质上讲,CMA 是一种更民主地知情交易决策的工具,确保没有单一价格点过度影响感知趋势。
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
def calculate_CMA(prices):
cumsum = np.cumsum(prices)
cma = cumsum / (np.arange(len(prices)) + 1)
return cma
# Fetching data
ticker_symbol = "KO"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Calculate CMA
cma_period = len(data['Close'])
data['CMA'] = calculate_CMA(data['Close'])
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['CMA'], label='CMA', color='blue')
plt.title(f'Chande Moving Average (CMA) of {ticker_symbol}')
plt.legend()
plt.grid()
plt.show()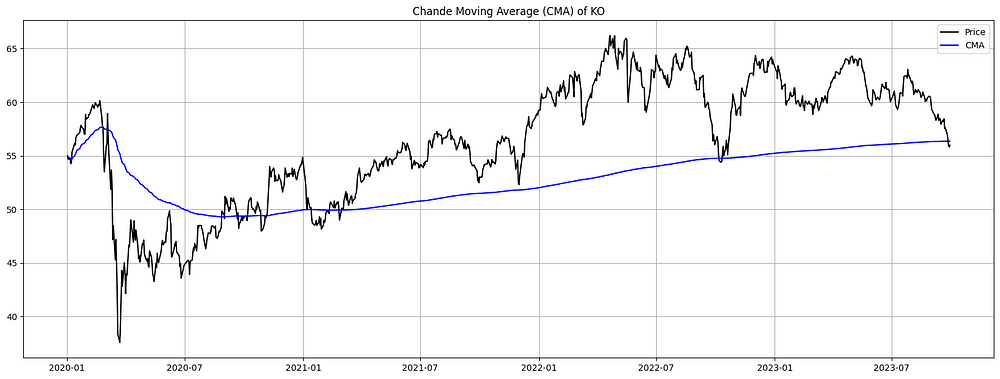
图 3. KO 的钱德移动平均线 (CMA)(2020-2023 年):CMA 本质上是收盘价的累积总和除以天数,因此它是考虑所有先前数据的移动平均线。图中显示了 Apple 的股价(黑色)和 CMA(蓝色)。CMA 给出了 AAPL 自成立以来的整体价格轨迹的平滑表示。
2.4 谐波移动平均线
谐波移动平均线是一种应用调和平均公式的移动平均线。与对数值之和进行平均的算术平均值不同,调和平均值是倒数的算术平均值的倒数。
它为较低的值提供比较高的值更多的权重。由于其独特的计算方式,HMA 可能会提供对价格趋势的不同见解,特别是当价格呈现特定模式或节奏时。
给定n 个周期的一系列价格p 1, p 2,…, pn :
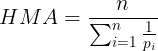
方程 2.4.1。调和移动平均线 (HMA) 公式:利用调和平均公式,HMA 通过应用倒数算术平均值的倒数来强调较低值而不是较高值。
对于交易者来说,谐波移动平均线 (HMA) 是一种有趣的工具,它强调价格较低的时期,可能比其他移动平均线更明显地突出买入机会或支撑位。这种独特的权重在价格回撤和盘整构成当前趋势重要组成部分的市场中尤其有用。
当与其他指标一起应用时,HMA 可以帮助识别价值期或抑价期。此外,在价格突然上涨可能会影响其他平均水平的波动市场中,HMA 保持相对稳定,更多地关注持续较低的价格点。
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
def calculate_HMA(prices, window):
hma_values = []
for i in range(len(prices)):
if i < window - 1:
hma_values.append(np.nan)
else:
subset_prices = prices[i - window + 1: i + 1]
harmonic_mean = window / np.sum([1/p for p in subset_prices])
hma_values.append(harmonic_mean)
return hma_values
# Fetching data
ticker_symbol = "MSFT"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Calculate HMA
hma_period = 20
data['HMA'] = calculate_HMA(data['Close'], hma_period)
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['HMA'], label=f'HMA {hma_period}', color='blue')
plt.title(f'Harmonic Moving Average (HMA) of {ticker_symbol} (n = {hma_period})')
plt.legend()
plt.grid()
plt.show()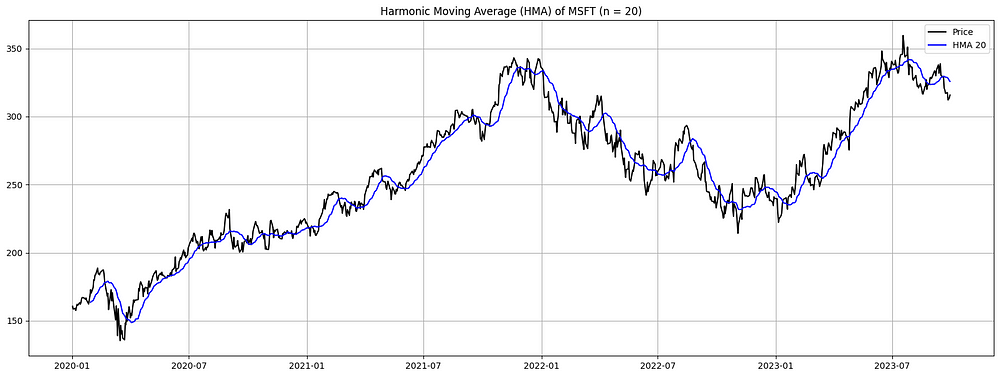
图 4. MSFT 的谐波移动平均线 (HMA)(2020-2023):HMA 由前 n 天收盘价倒数的算术平均值的倒数得出。对于此可视化,我们采用了 20 天的窗口。该图表显示了微软的股价(以黑色表示)与其 HMA(以蓝色表示)并列。HMA 通过对数据集中距离算术平均值更远的值给予更大的权重,提供对股票价格趋势的洞察,与传统平均值相比,提供了独特的视角。
2.5 麦金利动态
McGinley 动态移动平均线由 John R. McGinley 于 1990 年推出。它的设计目的是比其他移动平均线更能响应基础数据系列。其公式确保在快速变化的市场中更紧密地跟踪价格,并在变化较慢的市场中最大限度地减少价格分离。目标是避免市场波动,同时仍对市场趋势做出快速反应。
麦金利动态计算如下:

方程 2.5.1。麦金利动态移动平均线公式:这种先进的移动平均线公式由约翰·R·麦金利 (John R. McGinley) 提出,旨在通过最小化快速市场中的滞后并减少较慢趋势中的分离来更有效地跟踪价格。
在哪里:
- MD是麦金利动态值。
- 价格是当前价格。
- N是一个常数(通常与用于移动平均值的值相同,例如每日数据的 14 天)。
在交易领域,麦金利动态由于其自我调整机制而比传统移动平均线具有明显的优势。计算方法本质上考虑了市场变化的速度,使其更能适应实时条件。
这意味着交易者可以对 McGinley Dynamic 生成的信号更有信心,因为它不太可能产生错误信号或落后价格太远。无论市场速度如何,其密切跟踪资产价格的独特行为对于旨在利用短期价格差异的交易者来说可能是一个福音。
import yfinance as yf
import matplotlib.pyplot as plt
def calculate_mcginley_dynamic(prices, n):
MD = [prices[0]]
for i in range(1, len(prices)):
md_value = MD[-1] + (prices[i] - MD[-1]) / (n * (prices[i] / MD[-1])**4)
MD.append(md_value)
return MD
# Fetching data
ticker_symbol = "AAPL"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Calculate McGinley Dynamic
n = 14
data['McGinley Dynamic'] = calculate_mcginley_dynamic(data['Close'].tolist(), n)
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['McGinley Dynamic'], label=f'McGinley Dynamic {n}', color='blue')
plt.title(f'McGinley Dynamic of {ticker_symbol} (n={n})')
plt.legend()
plt.grid()
plt.show()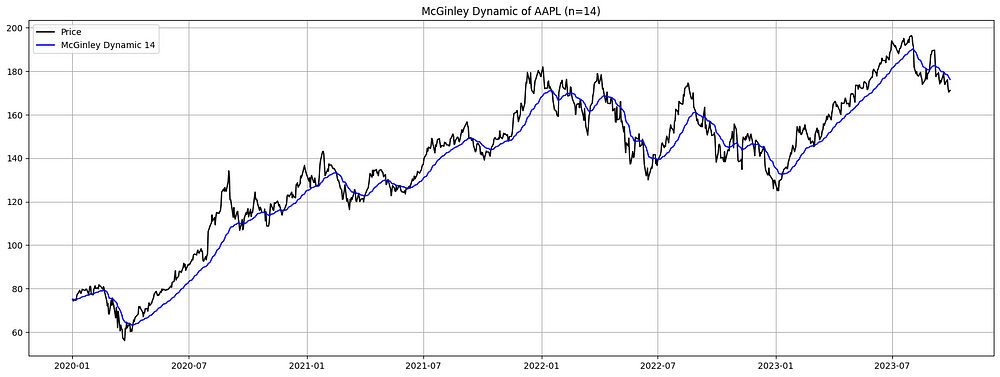
图 5. AAPL 的 McGinley Dynamic(2020-2023 年):McGinley Dynamic 旨在最大限度地减少滞后,适应 Apple 股价的快速变化。该图表显示了 14 天的时间段,将苹果的股价(黑色)与其麦金利动态(蓝色)进行了对比,展示了更平滑的价格走势。
2.6 锚定移动平均线
锚定移动平均线 (AMA) 是一种独特类型的移动平均线,它不是从系列中的第一个数据点开始计算,而是从特定的“锚定”点开始计算,通常是重要事件日期(例如,市场底部、突破、新闻发布等)。通过锚定移动平均线,重点在于该事件的重要性及其与价格走势的持续相关性。
公式:
AMA 的计算本质上是从锚定日期开始的简单移动平均线 (SMA):
![]()
方程 2.6.1。锚定移动平均线 (AMA) 的公式:AMA 通过从“锚定”点开始计算,对数据系列中的特定事件赋予重要性。
在哪里:
- AMAt是时间t的锚定移动平均线。
- 价格表示资产的价格。
- 锚定是锚定的时期。
锚定移动平均线通过强调特定事件,为交易者提供了一个观察价格相对于该重大事件如何演变的视角。收益公告、监管变化或宏观经济数据发布等事件可能会极大地改变市场情绪,AMA 会持续提醒该事件的市场影响。通过关注此类关键时刻的后果,交易者可以深入了解市场随时间对该事件的看法。
例如,如果在积极的盈利发布后价格持续保持在 AMA 上方,则表明持续的看涨情绪。相反,如果重大新闻事件发生后价格跌破 AMA,则可能表明普遍看跌观点。如果明智地使用,AMA 可以作为参考点,帮助交易者根据过去的重大事件了解最近的价格走势。
import yfinance as yf
import matplotlib.pyplot as plt
from matplotlib.dates import date2num
from datetime import datetime
def calculate_AMA(prices, anchor_date):
try:
anchor_idx = data.index.get_loc(anchor_date)
except KeyError:
# If the exact date is not found, find the nearest available date
anchor_date = data.index[data.index.get_loc(anchor_date, method='nearest')]
anchor_idx = data.index.get_loc(anchor_date)
AMA = []
for i in range(len(prices)):
if i < anchor_idx:
AMA.append(None)
else:
AMA.append(sum(prices[anchor_idx:i+1]) / (i - anchor_idx + 1))
return AMA
# Fetching data
ticker_symbol = "SIE.DE"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Define the anchor date
anchor_date = "2021-01-01"
anchor_date_num = date2num(datetime.strptime(anchor_date, '%Y-%m-%d'))
# Calculate AMA
data['AMA'] = calculate_AMA(data['Close'].tolist(), anchor_date)
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['AMA'], label='Anchored MA', color='red')
plt.axvline(x=anchor_date_num, color='blue', linestyle='--', label='Anchor Date')
plt.title(f'Anchored Moving Average (AMA) of {ticker_symbol}')
plt.legend()
plt.grid()
plt.show()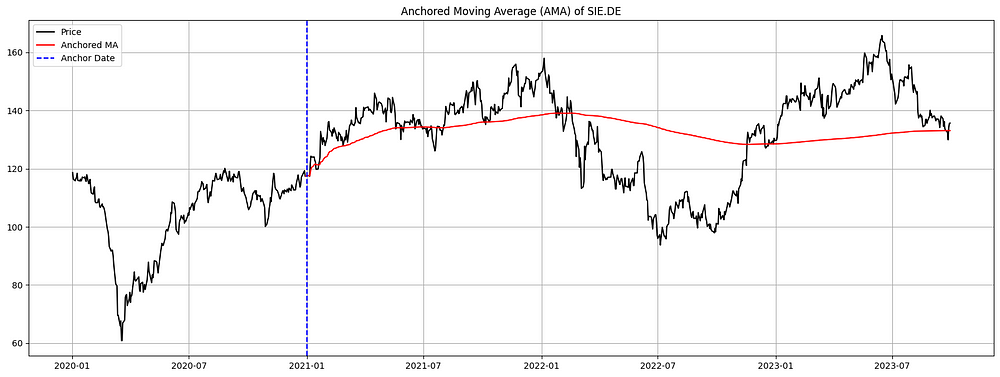
图 6. SAP.DE (2020–2023) 的锚定移动平均线 (AMA):AMA 从特定“锚定”日期开始计算,而不是滚动窗口。它将从该锚点到现在的所有数据进行平均。该图展示了 SAP 的股价(黑色)与其 AMA(红色),从蓝色虚线锚定日期开始。AMA 提供自重大事件或选定锚定日期以来价格趋势的见解。
2.7 霍尔特-温特斯移动平均线
Holt-Winters 方法包含三个方程:一个用于水平,一个用于趋势,一个用于季节性。每个方程都有一个平滑参数(alpha、beta、gamma),用于控制最近观察的权重。
级别 — 这是系列中的平均值。
![]()
方程 2.7.1。捕获平均值:水平(Lt)反映了时间序列的集中趋势,表示其平均值。平滑参数α确定最近观察的权重。
趋势 — 这是系列中增加或减少的值。
![]()
方程 2.7.2。检测方向变化:趋势 ( Tt ) 识别时间序列中随时间的一致向上或向下运动。它受到平滑参数β的影响,该参数考虑了最近的趋势演变。
季节性——这是系列中重复的短期周期。
![]()
方程 2.7.3。突出短期周期:季节性 ( St ) 表示在固定间隔内(通常在一年内)重复发生的周期性波动。它对最近循环模式的强调由平滑参数γ控制。
预报:
![]()
方程 2.7.4。预测未来值:该方程使用已确定的水平、趋势和季节性来预测时间序列的未来值。参数k指定预测提前了多少个周期。
在哪里:
- Lt是时间t时的水平。
- Tt是时间t的趋势。
- St是时间t的季节性。
- Yt是时间t的实际值。
- m是季节数。
- α、β、γ分别是水平、趋势和季节性的平滑参数。
- k是您要预测的未来周期数。
霍尔特温特斯与更基本的移动平均线的区别在于它能够动态适应趋势和季节性的变化。这种适应性正是它在时间序列数据表现出明显季节性模式的场景中受到青睐的原因,例如假期期间达到峰值的零售额或随季节变化的能源消耗。
应用 Holt-Winters 时,交易者和分析师应谨慎调整平滑参数 α、β 和 γ。这些参数决定了估计值对序列水平、趋势和季节性最近变化的响应程度。通过优化这些参数,可以在响应性和平滑性之间取得平衡。
import yfinance as yf
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# Fetching data
ticker_symbol = "INTC"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Fit the Holt-Winters model
model = ExponentialSmoothing(data['Close'], trend='add', seasonal='add', seasonal_periods=12)
fit = model.fit()
# Calculate HWMA
data['HWMA'] = fit.fittedvalues
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['HWMA'], label='HWMA', color='red')
plt.title(f'Holt-Winters Moving Average (HWMA) of {ticker_symbol}')
plt.legend()
plt.grid()
plt.show()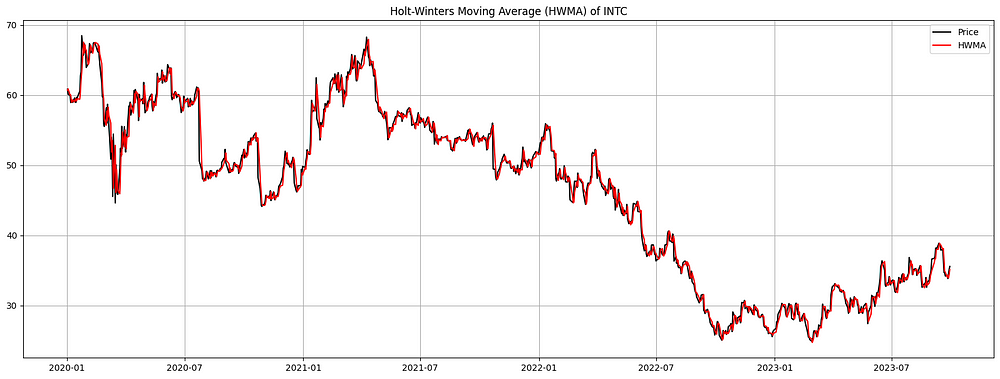
图 7. INTC 的 Holt-Winters 移动平均线 (HWMA)(2020-2023 年):HWMA(红色)采用指数平滑技术,考虑趋势和季节性,来描述 INTC 的股价变动。它根据实际收盘价(黑色)显示,提供对股票表现的基本趋势和潜在季节性的洞察。
2.8 过滤移动平均线
过滤移动平均线背后的概念是使用过滤机制(如数字或模拟过滤器)来消除数据集中的某些频率。这有助于强调特定频段(例如趋势),同时消除噪音。
FMA 定义为:
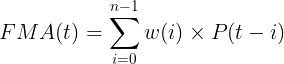
方程 2.8.1。强调趋势,减少噪音:过滤移动平均线 (FMA) 集成了一个过滤器机制,可以优先考虑某些频率,使其能够强调特定趋势并减少不需要的噪音。应用的权重w ( i ) 由所选滤波器的类型决定,而n表示移动平均周期。
在哪里:
- P ( t − i ) 是时间t − i的价格。
- w ( i ) 是时间t − i时价格的权重。具体权重取决于所应用的过滤器。
- n是移动平均线的周期。
过滤移动平均线(FMA)旨在强调数据集中的特定频段,有效增强潜在趋势的清晰度并减少短期波动的影响。这种方法通过减轻市场噪音的影响而提供了分析优势,市场噪音可能会掩盖真实的市场走势。
FMA 对优先频率的重视有助于区分市场情绪的实际变化和瞬态市场事件。FMA 的有效性取决于选择合适的滤波器和正确的周期 (n)。通过细化这些参数以匹配数据集的具体性质和战略目标,FMA 可以提供有关市场动态的更精确和可操作的见解。
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
def filtered_moving_average(prices, n=14):
# Define filter weights (for simplicity, we'll use equal weights similar to SMA)
w = np.ones(n) / n
return np.convolve(prices, w, mode='valid')
# Fetching data
ticker_symbol = "MCD"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
fma_period = 14
fma_values = filtered_moving_average(data['Close'].values, fma_period)
data['FMA'] = np.concatenate([np.array([np.nan]*(fma_period-1)), fma_values])
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['FMA'], label=f'Filtered MA {fma_period}', color='red')
plt.title(f'Filtered Moving Average (FMA) of {ticker_symbol} (n = {fma_period})')
plt.legend()
plt.grid()
plt.show()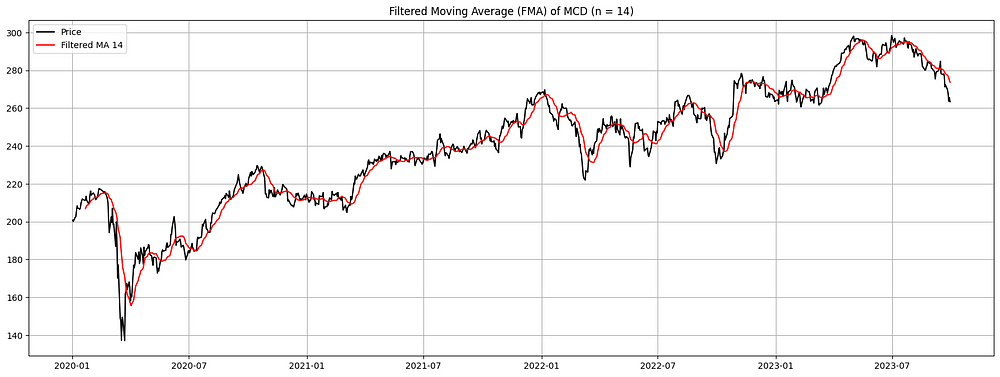
图 8. MCD (2020–2023) 的过滤移动平均线 (FMA):FMA(红色)本质上是一个简单的移动平均线,通过使用过滤器(在本例中为简单的等权重过滤器)进行了增强,以更好地强调某些数据特征。当根据麦当劳股票的实际收盘价(黑色)绘制时,FMA 可以更平滑地表示给定时期内的价格趋势,从而更容易辨别潜在的模式和走势。可以调整过滤器的选择以强调数据中的特定模式或特征。
2.9 Kijun Sen(基线)
Kijun Sen 也称为基线,代表特定时期(通常为 26 个时期)内最高点和最低点的中点。在 Ichimoku Cloud 设置中,Kijun Sen 有多种用途:
- 趋势指标:如果价格高于 Kijun Sen,则表明上升趋势,如果价格低于 Kijun Sen,则表明下降趋势。
- 支撑和阻力:Kijun Sen 充当支撑和阻力的动态水平。
- 买入或卖出信号:当移动速度较快的 Tenkan Sen(转换线)穿过 Kijun Sen 上方时,被视为看涨信号;当其穿过 Kijun Sen 下方时,则被视为看跌信号。
![]()
方程 2.9.1。Kijun Sen 或基线代表通常选择的 26 个周期跨度内的最高高点和最低低点之间的平衡
Kijun Sen 是 Ichimoku 云交易系统的一个组成部分,由于其多功能属性,在技术分析中具有非常重要的地位。它被计算为选定时间范围内最高点和最低点的中点,它本质上具有自我调整的性质,反映市场均衡和市场情绪的明确晴雨表。
此外,由于它对价格变动动态起作用,因此其提供实时支撑和阻力水平的能力对于进入和退出决策至关重要。从战略上讲,识别 Kijun Sen 和 Tenkan Sen 之间的交叉点可以帮助确定动量变化,从而指导交易策略。
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
def calculate_kijun_sen(data, period=26):
# Determine the highest high and the lowest low for the given period
high_prices = data['High'].rolling(window=period).max()
low_prices = data['Low'].rolling(window=period).min()
# Calculate Kijun Sen (Base Line)
kijun_sen = (high_prices + low_prices) / 2
return kijun_sen
# Fetching data
ticker_symbol = "WMT"
data = yf.download(ticker_symbol, start="2020-01-01", end="2024-01-01")
# Calculate Kijun Sen
data['Kijun Sen'] = calculate_kijun_sen(data)
# Plotting
plt.figure(figsize=(20,7))
plt.plot(data.index, data['Close'], label='Price', color='black')
plt.plot(data.index, data['Kijun Sen'], label='Kijun Sen (Base Line)', color='blue')
plt.title(f'Kijun Sen (Base Line) of {ticker_symbol}')
plt.legend()
plt.grid()
plt.show()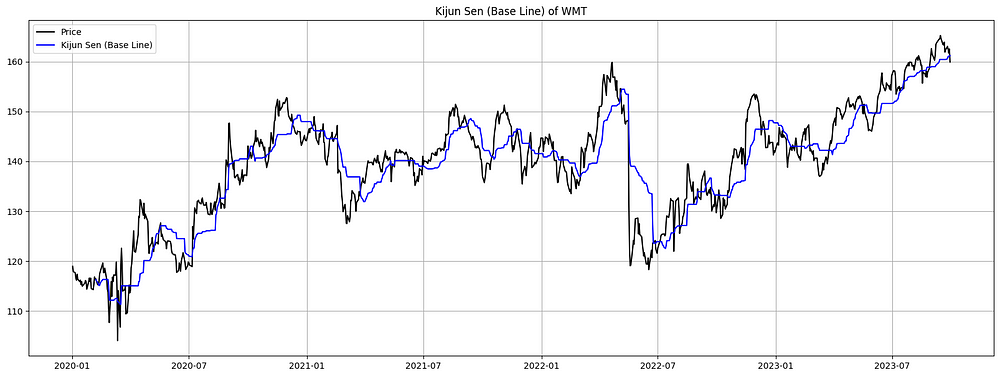
图 9. AAPL 的 Kijun Sen(基线)(2020-2023 年):Kijun Sen(蓝色)代表 26 个典型周期内最高点和最低点之间的平衡点。当根据苹果股票的实际收盘价(黑色)绘制时,Kijun Sen 充当动态参考线。高于 Kijun Sen 可能表明上升趋势,而低于 Kijun Sen 可能表明潜在的下降趋势。
3. 应用与见解
利基移动平均线技术为交易者提供了独特的市场视角,挑战他们超越传统范式的思考。例如,麦金利动态移动平均线有望成为最可靠的移动平均线,强调了对交易准确性的追求。
另一方面,霍尔特-温特斯移动平均线提供了一种预测方法,有助于预测分析。它结合使用指数平滑和季节性调整来生成对未来价格变动的预测。这使其成为寻求识别和利用市场趋势的交易者的宝贵工具。
以下是如何在交易中使用利基移动平均线技术的一些具体示例:
- 麦金利动态移动平均线可用于识别趋势和反转。它对于识别支撑位和阻力位也很有用。
- 霍尔特-温特斯移动平均线可用于生成对未来价格变动的预测。它还可用于识别市场的季节性模式。
4. 结论
每个交易者都配备了一套技术,虽然传统工具奠定了基础,但利基移动平均线通常会微调策略以接近完美。这些专业平均线因其适应性强且不易受错误信号影响而在波动的市场中表现出色,可提供独特的市场洞察。然而,它们也很复杂:复杂的计算和参数设置。
对于那些准备深入研究的人来说,这些利基技术有望增强市场理解、更好的策略制定和精细的风险管理。然而,它们并不能保证成功。当与健全的策略、情感纪律和强大的风险管理相结合时,他们的真正潜力就会被释放。