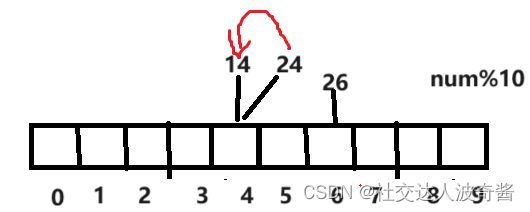
由选择器引发的疑问与思考
?想的是就让每位表示得越多,不就越能节省空间开销,从而不需要那么多的位数?
状态总量为S,R进制的N位数有S=R*N,
表示当前这个位数的进制数所能表示最多的状态总量

客观存在的数量在不同进制描述下不同,但是是同一个本质

之前理解的是,一位就是一个状态,每位上状态的不同使其记录不同的数
虽然事实确实如此
但是,但是,每位上数不是凭空产生的,而是选择出来的,即从提前记录的数字里面选出来的
如果是2进制,就需要提前记录2个,01来表示这个位上可能出现的所有情况
如果是10进制,就需要提前记录0~9来表示这个位上可能出现的情况,而不是9或8在这位上凭空产生
如果是100进制,就需要每位记录100个数
那么由S=N*R,R是进制,也是每位可能出现的所有情况,也就是计算机存储每位的代价
之前理解的是计算机存储每位的代价都是1,但实际上是R,即和进制,每位上出现的所有情况数有关
那么目的就是,用最少的计算机存储代价,来存储最多的状态总量
总代价为每位的代价*需要的位数
每位的代价越大(进制越大),需要的位数越小
代价越少(进制越小),需要的位数越大
(很像自适应逼近数组那个算法
那个是呈现代价大了,会使逼近成本小
呈现代价小了,逼近成本大)