目录

一、（leetcode 110）平衡二叉树

二、（leetcode 257）二叉树的所有路径

三、（leetcode 404）左叶子之和

---

一、（leetcode 110）平衡二叉树

力扣题目链接

状态：已AC

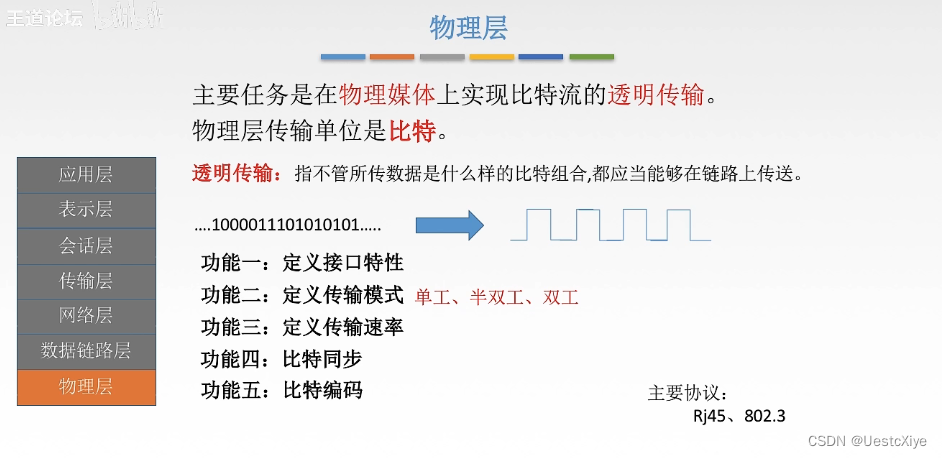
• 求深度可以从上到下去查，所以需要前序遍历（中左右）
• 高度只能从下到上去查，所以只能后序遍历（左右中）

通过这道题，对于树的「高度」和「深度」有了一些体会。高度是相对于叶子节点来说，大部分的递归都需要先走到叶子节点处再向上生长，这就有了高度的概念；而深度则是相对于根节点，在使用迭代方法计算二叉树高度的时候，程序从根节点往下走（层序），就有深度的感觉。

class Solution {
public:
    int getHeight(TreeNode* node){
        if(node == nullptr) return 0;
 
        int leftHeight = getHeight(node->left);
        if(leftHeight == -1) return -1;
        int rightHeight = getHeight(node->right);
        if(rightHeight == -1) return -1;

        return abs(leftHeight - rightHeight) > 1 ? -1 : 1+max(leftHeight, rightHeight);
    }
 
    bool isBalanced(TreeNode* root) {
        int height = getHeight(root);
        return height == -1 ? false : true;
    }
};

二、（leetcode 257）二叉树的所有路径

力扣题目链接

状态：了解思路后Debug AC。

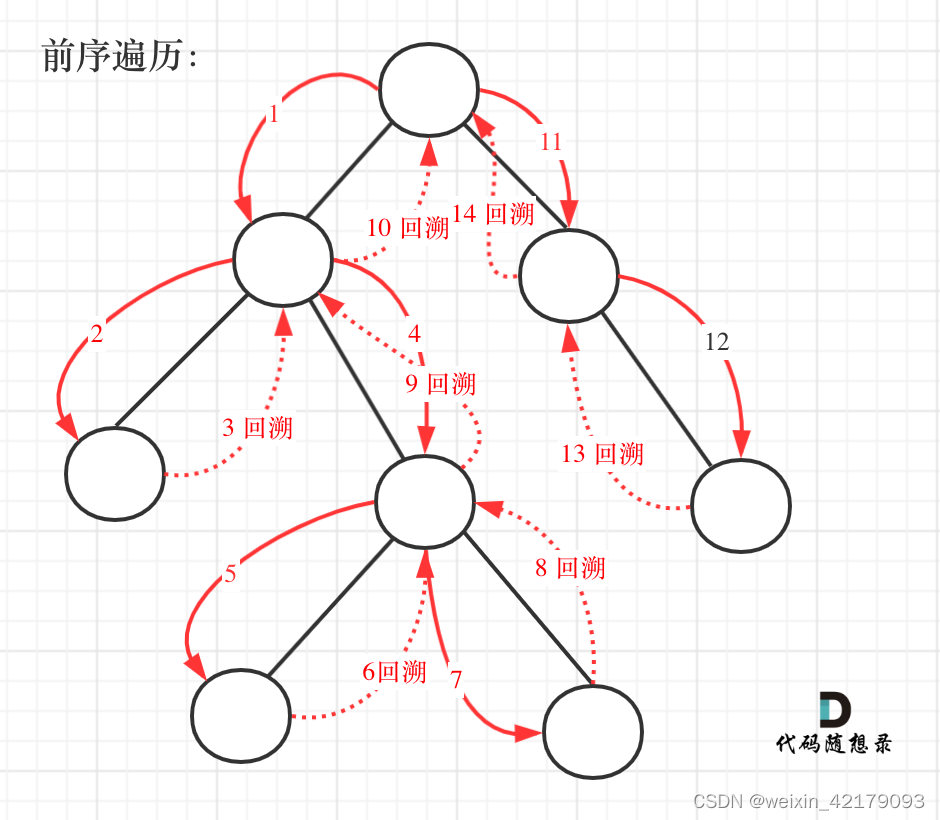
这道题用了回溯，和前两天的不一样。但是总体思路上是「确定递归终止条件」->「递归前进方式」->「回溯」。注意：「回溯和递归是一一对应的，有一个递归，就要有一个回溯」。这也是最大的收获。

class Solution {
public:
    void travelTree(TreeNode* node, vector<int>& path, vector<string>& res){
        if(node->left == nullptr && node->right == nullptr){
            string rPath = "";
            int len = path.size();
            for(int i = 0; i < len; ++i){
                rPath += to_string(path[i]);
                rPath += "->";
            }
            rPath += to_string(node->val);
            res.emplace_back(rPath);
        }
 
        path.emplace_back(node->val);
 
        if(node->left){
            travelTree(node->left, path, res);
            path.pop_back();
        }
        if(node->right){
            travelTree(node->right, path, res);
            path.pop_back();
        }
    }
 
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        vector<int> path;
 
        travelTree(root, path, res);
 
        return res;
    }
};

三、（leetcode 404）左叶子之和

力扣题目链接

状态：Debug后AC

可以继续利用回溯，回溯的关键就是要用一个数组来记录路径，然后每一次递归操作都要有一次路径的吐出操作（路径的增加在进入递归函数的时候会有）。对于本道题而言，需要注意的求的是左「叶子」节点，不是左孩子节点。

class Solution {
public:
    void travelTree(TreeNode* node, vector<TreeNode*>& path, int& lsum){
        if(node == nullptr) return;
        path.emplace_back(node);
        if(node->left){
            if(node->left->left == nullptr && node->left->right == nullptr){
                lsum += node->left->val;
            }
            travelTree(node->left, path, lsum);
            path.pop_back();
        }
        if(node->right){
            travelTree(node->right, path, lsum);
            path.pop_back();
        }
 
    }
 
    int sumOfLeftLeaves(TreeNode* root) {
        // 还是回溯的思想
        vector<TreeNode*> path;
        int lsum = 0;
        travelTree(root, path, lsum);
        return lsum;
    }
};