目录
前言
一、工作原理
二、模板
函数模板:
准备工作
三、主要应用
(一)寻找全部路径
题目描述
输入格式
输出格式
样例输入
样例输出
参考代码
思路
原题链接:1213: 走迷宫
(二)统计连通块数量
寻找连通分量
题目描述
样例输入
样例输出
参考代码
思路
原题链接:P1596 [USACO10OCT] Lake Counting S
四、易错点总结
前言
深度优先搜索,简称“深搜”,DFS,主要用于无向无权简单图的搜索工作,与广度优先搜索并称两大优先搜索算法,可以使用栈,也可以递归实现,数据量大用栈,小就用递归。
一、工作原理
深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法,它从根节点或起始节点开始,首先访问所有可到达的节点,然后对于每个可到达的节点,再递归地访问其未访问过的相邻节点,直到所有节点都被访问为止。
我们来仔细地看一下这个过程:

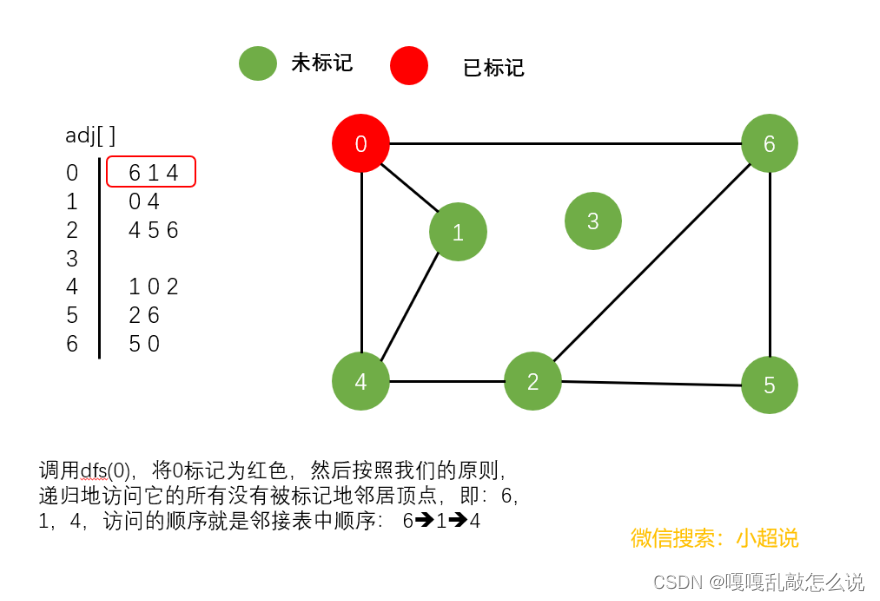








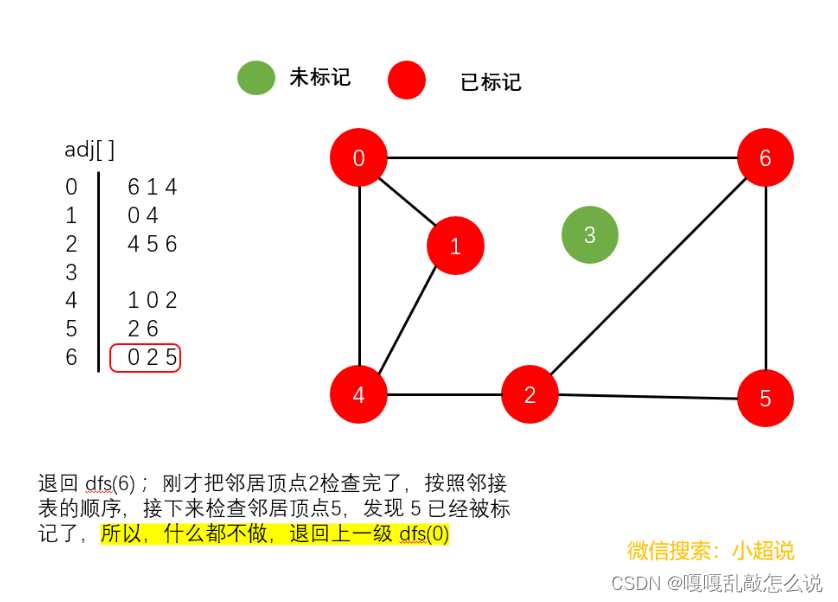

深度优先搜素大致可以这样描述:不撞南墙不回头,它沿着一条路一直走下去,直到走不动了然后返回上一个岔路口选择另一条路继续前进,一直如此,直到走完所有能够到达的地方!它的名字中深度两个字其实就说明了一切,每一次遍历都是走到最深!
注意一个细节:在我们上面的最后一个图中,顶点3仍然未被标记(绿色)。我们可以得到以下结论:
使用深度优先搜索遍历一个图,我们可以遍历的范围是所有和起点连通的部分,通过这一个结论,下文我们可以实现一个判断整个图连通性的方法。
深度优先搜索的代码实现,我是用Java实现的,其中,我定义了一个类,这样做的目的是更加清晰(毕竟,一会后面还有很多算法)
二、模板
函数模板:
void dfs(int x, int y)
{
if(出口)
{
退出或特殊操作
}
标记
for(主要是遍历所有方向 4、8...)
{
nx = x + dx[i]; //确定下一步的位置
ny = y + dy[i];
if(nx >= 0 && nx < n && ny >= 0 && ny < m && —特殊判断—)//判断下一步的位置是否合法?
{
标记数组为true
dfs(nx, ny); //递归
标记数组为false//递归结束回溯,不然会影响下一层递归的结果
}
}
}准备工作
int a[105][105]; //原数组
int dx[9] = {0, -1, 1, 0, 0, -1, -1, 1, 1}; //方向数组
int dy[9] = {0, 0, 0, -1, 1, -1, 1, -1, 1};
int vis[105][105]; //标记访问数组
int n, m; //其他变量三、主要应用
(一)寻找全部路径
我们通过深度优先搜索可以轻松地遍历一个图,如果我们在此基础上增加一些代码就可以很方便地查找图中的路径!
比如,题目给定顶点A和顶点B,让你求得从A能不能到达B?如果能,给出一个可行的路径!
据一道例题来说明一下:
题目描述
有一个n*m格的迷宫(表示有n行、m列),其中有可走的也有不可走的,如果用1表示可以走,0表示不可以走,文件读入这n*m个数据和起始点、结束点(起始点和结束点都是用两个数据来描述的,分别表示这个点的行号和列号)。现在要你编程找出所有可行的道路,要求所走的路中没有重复的点,走时只能是上下左右四个方向。如果一条路都不可行,则输出相应信息(用-1表示无路)。
请统一用 左上右下的顺序拓展,也就是 (0,-1),(-1,0),(0,1),(1,0)。
输入格式
第一行是两个数n,m( 1 < n , m < 15 ),接下来是n行m列由1和0组成的数据,最后两行是起始点和结束点。
输出格式
所有可行的路径,描述一个点时用(x,y)的形式,除开始点外,其他的都要用“->”表示方向。
如果没有一条可行的路则输出-1。
样例输入
5 6 1 0 0 1 0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 5 6样例输出
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6) (1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)参考代码
思路
这里呢,我先用vector存储每一步的路径,因为在运行时你是不确定它是否可以到达终点的,所以每一步都要存储,二维坐标系(x, y)所以需要结构体 node 搭配 vector十分的完美,print函数有一个细节大家要注意一下,在样例输入中,我们可以发现在每一条路径的结尾是没有箭头“->”的,所以要有一个小 if 判断一下,不然很有可能爆0的哦!
#include <iostream> #include <cstdio> #include <vector> #include <cstring> #define ll long long using namespace std; struct node { int x; int y; }; vector <node> v; int a[20][20], sx, sy, ex, ey, n, m; int dx[5] = {0, 0, -1, 0, 1}; int dy[5] = {0, -1, 0, 1, 0}; bool vis[20][20], vflag = false, flag = false; void print() { for(vector<node>::iterator iter = v.begin(); iter != v.end(); iter++) { if(iter + 1 == v.end()) cout<<"("<<iter->x<<","<<iter->y<<")"; else cout<<"("<<iter->x<<","<<iter->y<<")"<<"->"; } } void dfs(int x, int y) { vis[x][y] = true; node tmp; tmp.x = x; tmp.y = y; v.push_back(tmp); if(x == ex && y == ey) { flag = true; print(); cout<<endl; v.clear(); node tmp; tmp.x = sx; tmp.y = sy; v.push_back(tmp); return ; } for(int i = 1; i <= 4; i++) { int nx = x + dx[i]; int ny = y + dy[i]; if(nx >= 1 && nx <= n && ny >= 1 && ny <= m && !vis[nx][ny] && a[nx][ny] == 1) { vis[nx][ny] = true; dfs(nx, ny); vis[nx][ny] = false; for(vector<node>::iterator iter = v.begin(); iter != v.end(); ) { if(iter->x == tmp.x && iter->y == tmp.y) iter = v.erase(iter); else iter++; } } } } int main() { cin>>n>>m; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { cin>>a[i][j]; } } cin>>sx>>sy; cin>>ex>>ey; dfs(sx, sy); if(!flag) { cout<<"-1"<<endl; return 0; } return 0; }原题链接:1213: 走迷宫
感兴趣的伙伴可以去做一做,还是比较简单的!
(二)统计连通块数量
还记得我们上文讲到的dfs的一条性质吗?一个dfs搜索能够遍历与起点相连通的所有顶点。我们可以这样思考:申请一个整型数组id[0]用来将顶点分类——“联通的顶点的id相同,不连通的顶点的id不同”。首先,我对顶点adj[0]进行dfs,把所有能够遍历到的顶点的id设置为0,然后把这些顶点都标记;接下来对所有没有被标记的顶点进行dfs,执行同样的操作,比如将id设为1,这样依次类推,直到把所有的顶点标记。最后我们我们得到的id[]就可以完整的反映这个图的连通情况。
我们再举例一道题来说明一下:
题目描述
由于近期的降雨,雨水汇集在农民约翰的田地不同的地方。我们用一个 N×M (1 ≤ N ≤ 100,1 ≤ M ≤ 100) 的网格图表示。每个网格中有水(
W) 或是旱地(.)。一个网格与其周围的八个网格相连,而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图,确定当中有多少水坑。输入第 11 行:两个空格隔开的整数:N 和 M。
第 22 行到第 N+1 行:每行 M 个字符,每个字符是
W或.,它们表示网格图中的一排。字符之间没有空格。输出一行,表示水坑的数量。
样例输入
10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.样例输出
3参考代码
思路
这次是8方向遍历所以 dx 和 dy 数组需要更改,仍然还是模板直接往上套,我省去了vis标记数组,因为我们只需要把原数组s的坐标是水的位置一遍历到就改成空地,就简单轻松的做到了vis数组的全部功能。
#include <iostream> #include <cstdio> #define ll long long using namespace std; char s[105][105]; int dx[9] = {0, -1, 1, 0, 0, -1, -1, 1, 1}; int dy[9] = {0, 0, 0, -1, 1, -1, 1, -1, 1}; int n, m, ans = 0; bool flag = false; void dfs(int x, int y) { if(s[x][y] == 'W') { flag = true; } s[x][y] = '.'; int nx, ny; for(int i = 1; i <= 8; i++) { nx = x + dx[i]; ny = y + dy[i]; if((nx >= 0 && nx < n && ny >= 0 && ny < m) && s[nx][ny] == 'W') { flag = true; dfs(nx, ny); } } } int main() { scanf("%d%d", &n, &m); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { cin>>s[i][j]; } } for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { dfs(i, j); if (flag) { ans++; flag = false; } } } cout<<ans; return 0; }原题链接:P1596 [USACO10OCT] Lake Counting S
四、易错点总结
(一)方向数组
方向数组一定要写对,不然全盘乱透
//4方向,这里我是按照上、下、左、右的顺序进行的排列
int dx[5] = {0, -1, 1, 0, 0};
int dy[5] = {0, 0, 0, -1, 1};
//8方向,这里我是按照上、下、左、右、左上、右上、左下、右下的顺序进行的排列
int dx[9] = {0, -1, 1, 0, 0, -1, -1, 1, 1};
int dx[9] = {0, 0, 0, -1, 1, -1, 1, -1, 1};
//这里因为我是从1开始存储数组的,所以第一个要多垫一个0,记性好的老铁可以从0开始,但千万不要搞混!(二)一定要回溯!
除非题目已经要求每个坐标只能走一次,不然DFS一定要加回溯!!
vis[nx][ny] = true;
dfs(nx, ny);
vis[nx][ny] = false; //回溯!!假设第 i 轮你走完了,到第 i + 1轮的时候如果你不把vis[nx][ny]的true设为false的话等于你到第 i + 1轮还留着第 i 轮的标记,就会出现重大错误!!
好了,本期文章就到这里,喜欢的老铁可以给我点个小爱心鼓励一下我,你们的鼓励是我最大的动力!

你觉得这样辛苦的写博文不值得你点赞吗?