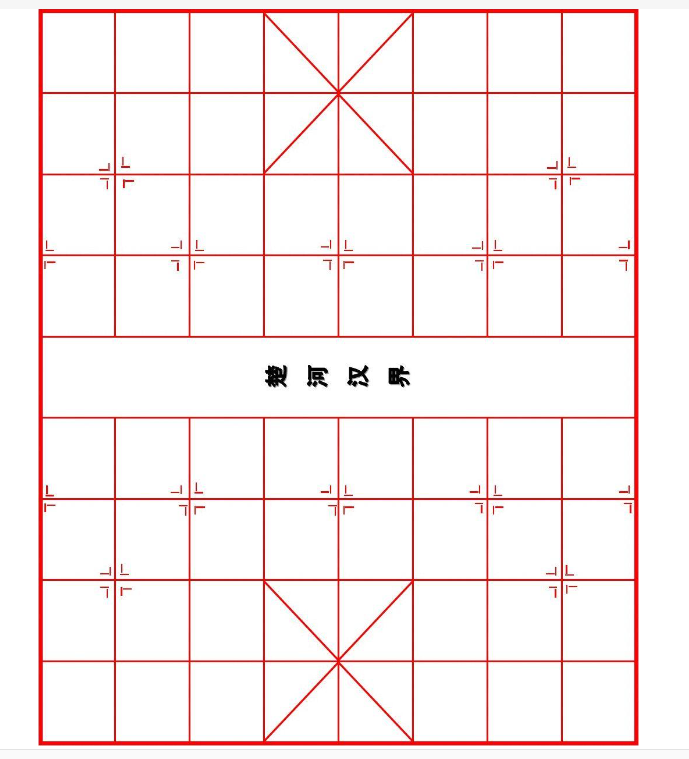
棋盘问题
将棋盘最左下角当作是平面直角坐标系的原点(0,0)位置,那么这个棋盘横坐标上就是9条线,纵坐标就是10条线,给定三个参数a、b、k,返回“马”从(0,0)位置出发,必须走K步,最后落在(a,b)上的方法数有多少种?
暴力递归
依然是先从暴力递归的方式开始分析,暴力递归方法要返回最大的方法数,而“马”在棋盘上可以向四周8个方向随意跳动,所以需要将每种方向跳动的结果集方法数进行累加。
base case:
第一个是当“马” 跳出棋盘范围。
第二个是当剩余 步数 为 0,此时如果正好落在(x,y)的位置,证明有一种方法。
//主方法,马从(0,0)位置开始跳
public static int jump(int a, int b, int k) {
return process(0, 0, k, a, b);
}
//返回最大方法数
//x,y 当前马的位置
//a,b 目标位置
//rest 剩余步数
public static int process(int x, int y, int rest, int a, int b) {
// 当马跳出棋盘范围,return 0
if (x > 8 || x < 0 || y > 9 || y < 0) {
return 0;
}
//当步数为0时,如果落在了 ab位置,说明有一种方法数
if (rest == 0) {
return (x == a) && (y == b) ? 1 : 0;
}
int ways = 0;
//马每次都可以在棋盘上向四周8个方向跳。将所有方法数累加。
//每跳一次,步数 - 1,x,y根据 象棋中 马走日的规则进行调整
ways += process(x + 2, y + 1, rest - 1, a, b);
ways += process(x - 2, y + 1, rest - 1, a, b);
ways += process(x - 1, y + 2, rest - 1, a, b);
ways += process(x + 1, y + 2, rest - 1, a, b);
ways += process(x - 2, y - 1, rest - 1, a, b);
ways += process(x + 2, y - 1, rest - 1, a, b);
ways += process(x - 1, y - 2, rest - 1, a, b);
ways += process(x + 1, y - 2, rest - 1, a, b);
return ways;
}
动态规划
继续根据暴力递归方法来改写动态规划,暴力递归方法中的可变参数为x,y和k,步数每次 - 1 ,xy是马的当前位置。所以这个dp表的构建和以往不同,是个三维数组。
接下来确定数组大小:
- k是步数,并且可以步数为0,所以k的 范围是 K + 1。
- xy是当前马的位置,并且只能在棋盘范围内跳动所以xy的大小是9,10
- 所以dp表的整体大小是 dp[9][10][K + 1]。
接下来根据暴力递归中的base case来给数组进行初始化赋值。
当rest剩余步数为0时,如果此时xy正好在ab上,则方法数为1。所以 dp[a][b][0] == 1。
因为是3维数组,所以先填充最底层的rest,根据是rest的依赖关系来确定xy的值,而根据暴力递归代码可以看出,rest是每次 - 1,所以从0开始填充。
代码
代码中需要注意的是pick方法,因为马可能会跳出棋盘,遇到这种情况不用统计,利用pick进行过滤即可。
public static int dp(int a, int b, int k) {
int[][][] dp = new int[9][10][k + 1];
dp[a][b][0] = 1;
for (int rest = 1; rest <= k; rest++) {
for (int x = 0; x < 9; x++) {
for (int y = 0; y < 10; y++) {
int ways = pick(dp,x + 2, y + 1, rest - 1);
ways += pick(dp,x - 2, y + 1, rest - 1);
ways += pick(dp,x - 1, y + 2, rest - 1);
ways += pick(dp,x + 1, y + 2, rest - 1);
ways += pick(dp,x - 2, y - 1, rest - 1);
ways += pick(dp,x + 2, y - 1, rest - 1);
ways += pick(dp,x - 1, y - 2, rest - 1);
ways += pick(dp,x + 1, y - 2, rest - 1);
dp[x][y][rest] = ways;
}
}
}
return dp[0][0][k];
}
public static int pick(int[][][] dp, int x, int y, int rest) {
if (x > 8 || x < 0 || y > 9 || y < 0) {
return 0;
}
return dp[x][y][rest];
}