代码随想录第39天 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

198.打家劫舍

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
  //dp[i]+=max(dp[i-2],dp[dp-3])
    if(nums.length===2)
    return Math.max(nums[0],nums[1])
  let dp=new Array(nums).fill(0)
  dp[0]=nums[0]
  dp[1]=Math.max(nums[0],nums[1])
  for(let i=2;i<nums.length;i++)
  {
      dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i])
  }
  return dp[nums.length-2]
};

第一想法

dp[i]代表一共有i个房子，我偷的最大数量
dp[i]=max（dp[i-1]，dp[i-2]+nums[i]）
如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）
dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出，递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1]);

213.打家劫舍II

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(arr) {

if(arr.length===1)
return arr[0]
// 情况1无头，return  nums[nums.length-1]
let a=function(nums){  
    if(nums.length===2)
    return Math.max(nums[0],nums[1])
  let dp=new Array(nums).fill(0)
  dp[0]=nums[0]
  dp[1]=Math.max(nums[0],nums[1])
  for(let i=2;i<nums.length;i++)
  {
      dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i])
  }
  return dp[nums.length-2]}

  return Math.max(a(arr),a(arr.reverse()))
};

思想

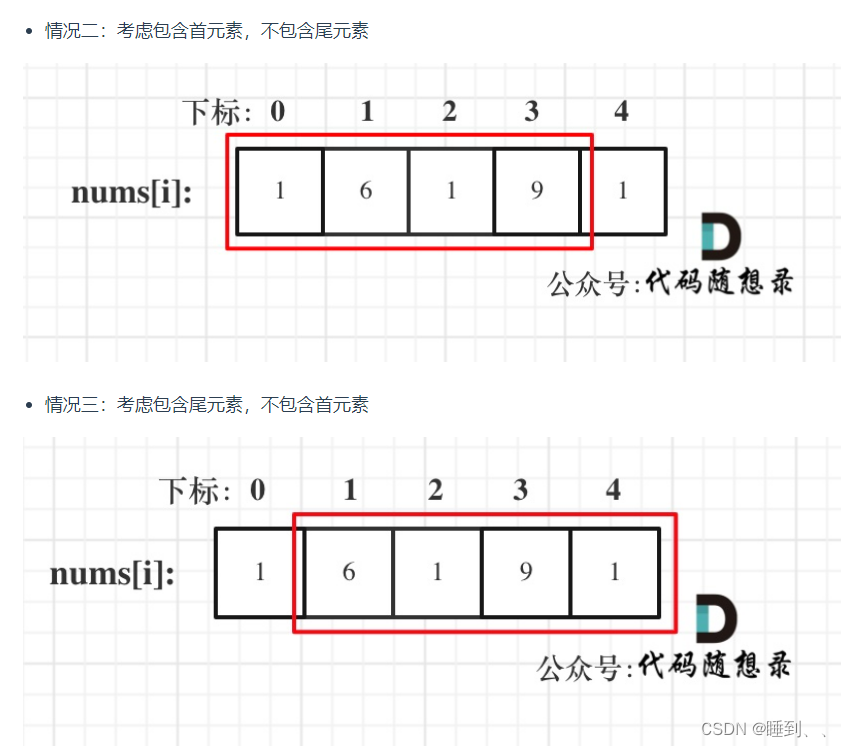
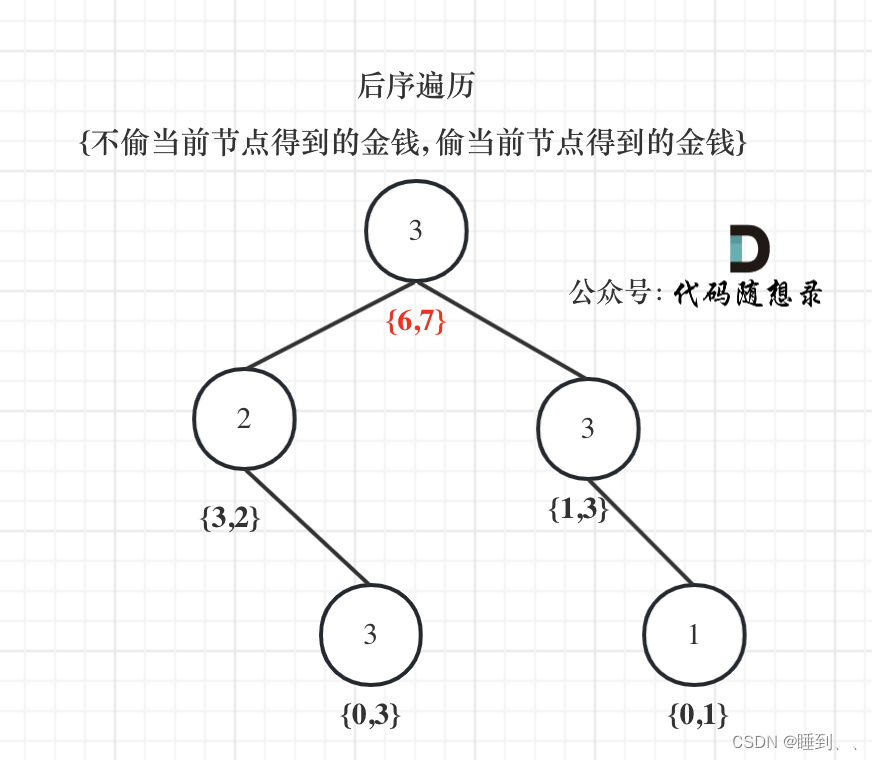
在这里插入图片描述

337.打家劫舍III

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var rob = function(root) {
//  后序遍历  左右中
const postOrder=node=>{
    // 递归出口
    if(!node) return [0,0]
    // 左
    const left=postOrder(node.left)
    // 右
    const right=postOrder(node.right)
    // 不偷当前节点，左右子节点都可以偷或不偷，取最大值
    const DoNot=Math.max(left[0],left[1])+Math.max(right[0],right[1])
    // 偷当前节点，左右子节点只能不偷
     const Do = node.val + left[0] + right[0];
        // [不偷，偷]
    return [DoNot, Do];
}
const res=postOrder(root)
// 返回最大值

return Math.max(...res)
};

思想

后序遍历+dp

确定递归函数的参数和返回值

返回数组就是dp数组,下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

确定终止条件
在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回

if(!node) return [0,0]

确定遍历顺序
后序遍历
通过递归左节点，得到左节点偷与不偷的金钱。
通过递归右节点，得到右节点偷与不偷的金钱。
中
确定单层递归的逻辑

// 不偷当前节点，左右子节点都可以偷或不偷，取最大值
const DoNot=Math.max(left[0],left[1])+Math.max(right[0],right[1])
// 偷当前节点，左右子节点只能不偷
const Do = node.val + left[0] + right[0];
// [不偷，偷]
return [DoNot, Do];