文章目录
- 1.决策树划分原理
- 1.1.特征选择1--信息增益
- 1.2.特征选择2--信息增益比
- 1.3.特征选择3--基尼系数
- 2.决策树属性划分计算题
- 2.1.信息增益计算
- 2.2.1.属性1的信息增益计算
- 2.2.2.属性2的信息增益计算
- 2.2.3.属性信息增益比较
- 2.2.信息增益比计算
- 2.3.基尼系数计算
1.决策树划分原理
在决策树的算法中,我们常用的划分属性的方法又如下三种:
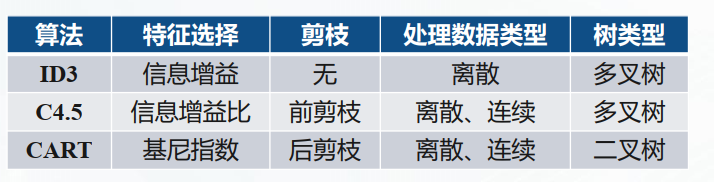
那么我们是怎么通过特征选择指标来进行属性的划分的呢,我们接下来将介绍上述三个特征选择的划分算法。
1.1.特征选择1–信息增益
“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标假定当前样本集合D中第k类样本所占的比例为
p
k
(
k
=
1
,
2
,
.
.
.
,
)
p_{k}(k = 1,2,...,)
pk(k=1,2,...,) ,则D的信息熵定义为
Ent
(
D
)
=
−
∑
k
=
1
∣
Y
∣
p
k
log
2
p
k
.
\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|}p_{k}\log_{2}p_{k}.
Ent(D)=−k=1∑∣Y∣pklog2pk.
假定离散属性a有V个可能的取值
{
a
1
,
a
2
,
a
3
,
.
.
.
.
a
v
}
\{{a^{1},a^{2},a^{3},....a^{v}}\}
{a1,a2,a3,....av},若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D 中所有在属性a上取值为
a
v
a^{v}
av的样本记为
D
v
D^{v}
Dv,我们可根据计算D信息再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重
D
v
/
D
D^{v}/D
Dv/D即样本数越多的分支结点的影响越大于是可计算出用属性a对样本D进行划分所获得的“信息增益”(information gain)。
G
a
i
n
(
D
,
a
)
=
E
n
t
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
E
n
t
(
D
v
)
\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}\mathrm{Ent}(D^{v})
Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大.因此,我们可用信息增益来进行决策树的划分属性选择。
1.2.特征选择2–信息增益比
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响著名的 C4.5 决策算法不直接使用信息增益而是使用“增益率”(gain ratio)来选择最优划分属性,增益率定义如下所示:
G
a
i
n
_
r
a
t
i
o
(
D
,
a
)
=
G
a
i
n
(
D
,
a
)
I
V
(
a
)
\mathrm{Gain}\_\mathrm{ratio}(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)}
Gain_ratio(D,a)=IV(a)Gain(D,a)
其中,
I
V
(
a
)
=
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
log
2
∣
D
v
∣
∣
D
∣
\mathrm{IV}(a)=-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}\log_{2}\frac{|D^{v}|}{|D|}
IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性a的“固有值”(intrinsic value),属性a的可能取值数目越多(即 V 越大)则IV(a) 的值通常会越大。
需注意的是,增益率准则对可取值数目较少的属性有所偏好,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性再从中选择增益率最高的.
1.3.特征选择3–基尼系数
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼值的计算公式如下所示:
G
i
n
i
(
D
)
=
∑
k
=
1
∣
Y
∣
∑
k
′
≠
k
p
k
p
k
′
=
1
−
∑
k
=
1
∣
Y
∣
p
k
2
.
\begin{aligned}\mathrm{Gini}(D)&=\sum_{k=1}^{|\mathcal{Y}|}\sum_{k^{\prime}\neq k}p_kp_{k^{\prime}}\\&=1-\sum_{k=1}^{|\mathcal{Y}|}p_k^2.\end{aligned}
Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2.
直观来说,Gini(D)反映了从数据集 D中随机抽取两个样本,其类别标记不一致的概率。因此Gini(D)越小则数据集 D的纯度越高,基尼指数定义如下所示:
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
=
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
.
G
i
n
i
(
D
v
)
\mathrm{Gini}\_\mathrm{index}(D,a)=\sum_{v=1}^{V}\frac{|D^{v}|}{|D|.}\mathrm{Gini}(D^{v})
Gini_index(D,a)=v=1∑V∣D∣.∣Dv∣Gini(Dv)
于是,我们在候选属性集合 A 中选择那个使得划分后基尼指数最小的属性作为最优划分属性。
2.决策树属性划分计算题
Iris数据集的某个特征增广版本包含7个样本,具体情况如表格示对比香气和颜色两种特征,分别依据信息增益、 信息增益比和基尼指数给出分裂特征选择结果及计算过程。
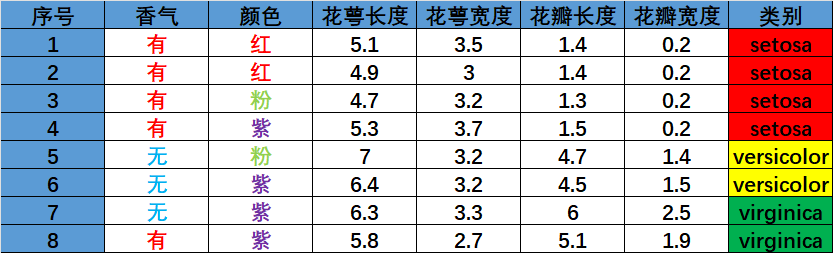
2.1.信息增益计算
2.2.1.属性1的信息增益计算
首先计算根结点的信息熵,根据类别区分出setosa有4朵,versicolor有2朵,virginica有2朵,则根节点的信息熵计算如下:
E
n
t
(
D
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
4
8
l
o
g
2
4
8
+
2
8
l
o
g
2
2
8
+
2
8
l
o
g
2
2
8
)
=
1.5
Ent(D)=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{4}{8}log_{2}\frac{4}{8}+\frac{2}{8}log_{2}\frac{2}{8}+\frac{2}{8}log_{2}\frac{2}{8} )=1.5
Ent(D)=−k=1∑3pklog2pk=−(84log284+82log282+82log282)=1.5
针对酒香类型,S={有酒香,无酒香},我们分别计算该属性的信息熵如下所示:
E
n
t
(
S
1
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
4
5
l
o
g
2
4
5
+
0
l
o
g
2
0
+
1
5
l
o
g
2
1
5
)
=
0.721
Ent(S^{1})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{4}{5}log_{2}\frac{4}{5}+0log_{2}0+\frac{1}{5}log_{2}\frac{1}{5} )=0.721
Ent(S1)=−k=1∑3pklog2pk=−(54log254+0log20+51log251)=0.721
E
n
t
(
S
2
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
0
3
l
o
g
2
0
3
+
2
3
l
o
g
2
2
3
+
1
3
l
o
g
2
1
3
)
=
0.918
Ent(S^{2})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{0}{3}log_{2}\frac{0}{3}+\frac{2}{3}log_{2}\frac{2}{3}+\frac{1}{3}log_{2}\frac{1}{3} )=0.918
Ent(S2)=−k=1∑3pklog2pk=−(30log230+32log232+31log231)=0.918
最后我们计算酒香属性的信息增益值,如下所示:
Gain
(
D
,
S
)
=
Ent
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Ent
(
D
v
)
=
1.5
−
5
8
E
n
t
(
D
1
)
−
3
8
E
n
t
(
D
2
)
=
0.705
\operatorname{Gain}(D,S)=\operatorname{Ent}(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}\operatorname{Ent}(D^v)=1.5-\frac{5}{8}Ent(D^{1})-\frac{3}{8}Ent(D^{2})=0.705
Gain(D,S)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)=1.5−85Ent(D1)−83Ent(D2)=0.705
2.2.2.属性2的信息增益计算
针对颜色类型,S={红色,粉色,紫色},我们分别计算该属性的信息熵如下所示:
E
n
t
(
S
1
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
2
2
l
o
g
2
2
2
+
0
l
o
g
2
0
)
=
0
Ent(S^{1})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{2}{2}log_{2}\frac{2}{2}+0log_{2}0 )=0
Ent(S1)=−k=1∑3pklog2pk=−(22log222+0log20)=0
E
n
t
(
S
2
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
1
2
l
o
g
2
1
2
+
1
2
l
o
g
2
1
2
)
=
1
Ent(S^{2})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{1}{2}log_{2}\frac{1}{2}+\frac{1}{2}log_{2} \frac{1}{2})=1
Ent(S2)=−k=1∑3pklog2pk=−(21log221+21log221)=1
E
n
t
(
S
3
)
=
−
∑
k
=
1
3
p
k
l
o
g
2
p
k
=
−
(
1
4
l
o
g
2
1
4
+
1
2
l
o
g
2
1
2
+
1
2
l
o
g
2
1
2
)
=
1.5
Ent(S^{3})=-\sum_{k=1}^{3}p_{k}log_{2}p_{k}=-(\frac{1}{4}log_{2}\frac{1}{4}+\frac{1}{2}log_{2}\frac{1}{2}+ \frac{1}{2}log_{2}\frac{1}{2})=1.5
Ent(S3)=−k=1∑3pklog2pk=−(41log241+21log221+21log221)=1.5
最后我们计算颜色属性的信息增益值,如下所示:
Gain
(
D
,
S
)
=
Ent
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Ent
(
D
v
)
=
1.5
−
2
8
E
n
t
(
S
1
)
−
2
8
E
n
t
(
S
2
)
−
4
8
E
n
t
(
S
3
)
=
0.5
\operatorname{Gain}(D,S)=\operatorname{Ent}(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}\operatorname{Ent}(D^v)=1.5-\frac{2}{8}Ent(S ^{1})-\frac{2}{8}Ent(S^{2})-\frac{4}{8}Ent(S^{3})=0.5
Gain(D,S)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)=1.5−82Ent(S1)−82Ent(S2)−84Ent(S3)=0.5
2.2.3.属性信息增益比较
我们分别求出了酒香和颜色两种属性的信息增益,接下来我们就根据求出的信息增益来划分属性:
Gain
(
D
,
"
酒香
"
)
>
Gain
(
D
,
"
颜色
"
)
\operatorname{Gain}(D,"酒香")>\operatorname{Gain}(D,"颜色")
Gain(D,"酒香")>Gain(D,"颜色")
所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。
2.2.信息增益比计算
由上述分析我们知道信息增益和信息增益比的关系,所以我们直接计算信息增益比的值,如下所示:
H
^
{
"
酒香
"
}
=
−
∑
k
=
1
2
N
k
N
l
o
g
2
N
k
N
=
−
(
5
8
l
o
g
2
5
8
+
3
8
l
o
g
2
3
8
)
=
0.954
\hat{H}\{"酒香"\}=-\sum_{k=1}^{2}\frac{N_{k}}{N}log_{2}\frac{N_{k}}{N} =-(\frac{5}{8}log_{2}\frac{5}{8}+\frac{3}{8}log_{2}\frac{3}{8})=0.954
H^{"酒香"}=−k=1∑2NNklog2NNk=−(85log285+83log283)=0.954
H
^
{
"
颜色
"
}
=
−
∑
k
=
1
2
N
k
N
l
o
g
2
N
k
N
=
−
(
2
8
l
o
g
2
2
8
+
2
8
l
o
g
2
2
8
+
4
8
l
o
g
2
4
8
)
=
1.5
\hat{H}\{"颜色"\}=-\sum_{k=1}^{2}\frac{N_{k}}{N}log_{2}\frac{N_{k}}{N} =-(\frac{2}{8}log_{2}\frac{2}{8}+\frac{2}{8}log_{2}\frac{2}{8}+\frac{4}{8}log_{2}\frac{4}{8})=1.5
H^{"颜色"}=−k=1∑2NNklog2NNk=−(82log282+82log282+84log284)=1.5
由此我们能够计算出对应的信息增益比如下所示:
{
R
1
=
G
r
a
i
n
(
D
,
"
酒香
"
)
H
^
{
"
酒香
"
}
=
0.705
0.954
=
0.738
R
2
=
G
r
a
i
n
(
D
,
"
颜色
"
)
H
^
{
"
颜色
"
}
=
0.5
1.5
=
1
3
\left\{\begin{matrix}R_{1}=\frac{Grain(D,"酒香")}{\hat{H}\{"酒香"\}} =\frac{0.705}{0.954}=0.738 \\R_{2}=\frac{Grain(D,"颜色")}{\hat{H}\{"颜色"\}} =\frac{0.5}{1.5}=\frac{1}{3}\end{matrix}\right.
{R1=H^{"酒香"}Grain(D,"酒香")=0.9540.705=0.738R2=H^{"颜色"}Grain(D,"颜色")=1.50.5=31
因为计算出的R1>R2,所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。
2.3.基尼系数计算
Gini系数的计算也比较简答,我们只要根据基尼系数的计算公式来进行计算即可:
计算酒香属性的Gini系数如下所示:
G
i
n
i
(
"
香气
"
=
"
有
"
)
=
1
−
∑
1
2
p
k
2
=
1
−
(
4
5
)
2
−
(
1
5
)
2
=
0.320
G
i
n
i
(
"
香气
"
=
"
无
"
)
=
1
−
∑
1
2
p
k
2
=
1
−
(
1
3
)
2
−
(
2
3
)
2
=
0.444
\begin{matrix}Gini("香气"="有")=1-\sum_{1}^{2}p^{2}_{k} =1-(\frac{4}{5} )^{2}-(\frac{1}{5} )^{2}=0.320 \\Gini("香气"="无")=1-\sum_{1}^{2}p^{2}_{k} =1-(\frac{1}{3} )^{2}-(\frac{2}{3} )^{2}=0.444\end{matrix}
Gini("香气"="有")=1−∑12pk2=1−(54)2−(51)2=0.320Gini("香气"="无")=1−∑12pk2=1−(31)2−(32)2=0.444
计算颜色属性的Gini系数如下所示:
G
i
n
i
(
"
颜色
"
=
"
红
"
)
=
1
−
∑
1
3
p
k
2
=
1
−
(
2
2
)
2
−
0
−
0
=
0
G
i
n
i
(
"
颜色
"
=
"
粉
"
)
=
1
−
∑
1
3
p
k
2
=
1
−
(
1
2
)
2
−
(
1
2
)
2
−
0
=
0.5
G
i
n
i
(
"
颜色
"
=
"
紫
"
)
=
1
−
∑
1
3
p
k
2
=
1
−
(
1
4
)
2
−
(
1
4
)
2
−
(
2
4
)
2
=
0.625
\begin{matrix}Gini("颜色"="红")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{2}{2} )^{2}-0-0=0 \\Gini("颜色"="粉")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{1}{2} )^{2}-(\frac{1}{2} )^{2}-0=0.5 \\Gini("颜色"="紫")=1-\sum_{1}^{3}p^{2}_{k} =1-(\frac{1}{4} )^{2}-(\frac{1}{4} )^{2}-(\frac{2}{4} )^{2}=0.625 \end{matrix}
Gini("颜色"="红")=1−∑13pk2=1−(22)2−0−0=0Gini("颜色"="粉")=1−∑13pk2=1−(21)2−(21)2−0=0.5Gini("颜色"="紫")=1−∑13pk2=1−(41)2−(41)2−(42)2=0.625
由此我们分别计算对应的基尼系数如下所示:
G
i
n
i
_
R
a
t
i
o
(
"
香气
"
)
=
5
8
G
i
n
i
1
+
3
8
G
i
n
i
2
=
0.37
G
i
n
i
_
R
a
t
i
o
(
"
颜色
"
)
=
2
8
G
i
n
i
1
+
2
8
G
i
n
i
2
+
4
8
G
i
n
i
3
=
0.437
\begin{matrix}Gini\_Ratio("香气")=\frac{5}{8} Gini_{1}+\frac{3}{8} Gini_{2}=0.37 \\Gini\_Ratio("颜色")=\frac{2}{8} Gini_{1}+\frac{2}{8} Gini_{2}+\frac{4}{8} Gini_{3}=0.437\end{matrix}
Gini_Ratio("香气")=85Gini1+83Gini2=0.37Gini_Ratio("颜色")=82Gini1+82Gini2+84Gini3=0.437
因为计算出的
G
i
n
i
_
R
a
t
i
o
(
"
香气
"
)
Gini\_Ratio("香气")
Gini_Ratio("香气")<
G
i
n
i
_
R
a
t
i
o
(
"
颜色
"
)
Gini\_Ratio("颜色")
Gini_Ratio("颜色"),所以我们的选择的属性就是酒香,通过酒香的分类去划分属性。