​📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：练题
🎯长路漫漫浩浩，万事皆有期待

找树左下角的值

513. 找树左下角的值 - 力扣（LeetCode）

寻找树的左下角值，这里的左下角值指的是该树的最后一行中的最靠左节点，一定不要理解错误，两个条件缺一不可，最容易的一个方法是广搜来遍历到树的最后一层然后直接取该层的第一个节点即可，也可以用深搜，不过稍显麻烦。

class Solution {
public:
    int maxDepth=INT_MIN;
    int result;
    void traversal(TreeNode* root,int depth)
    {
        if(root->left==nullptr&&root->right==nullptr)
        {
            if(depth>maxDepth)
            {
                maxDepth=depth;
                result=root->val;
            }
            return;
        }
        if(root->left)
        {
            traversal(root->left,depth+1);
        }
        if(root->right)
        {
            traversal(root->right,depth+1);
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        traversal(root,0);
        return result;
    }
};

深搜的思路是：使用递归，结束条件是碰到叶子节点即判断一下，该层是否为最深，如果不是最深那么略过去，如果是最深的话取一下当前节点。这里不需要担心我们取的当前节点是否是该层第一个，原因是首先我们定义一个全局变量来指出当前所遍历过的最深有多深，第二点我们一定会先遍历到最左侧。

class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*> q;
        int result;
        q.push(root);
        while(!q.empty())
        {
            int size=q.size();
            for(int i=0;i<size;i++)
            {
                TreeNode*cur=q.front();q.pop();
                if(i==0)result=cur->val;//存储的是每一行的第一个元素
                if(cur->left)q.push(cur->left);
                if(cur->right)q.push(cur->right);
            }
        }
        return result;
    }
};

上述代码是广搜的思路，思路具体为将头节点先加入队列中，然后根据广搜的模板代码写出剩余过程，也就是先将队列头部节点取出，把它的左右子树都加入进来，需要在模板代码内加入的新东西是，我们需要做一个判断确保每一次第一个遍历到的最左节点数值能够直接存入在变量中（由于广搜的特性，所以我们遍历的每层第一个元素一定是最左边的）。

路径总和

112. 路径总和 - 力扣（LeetCode）

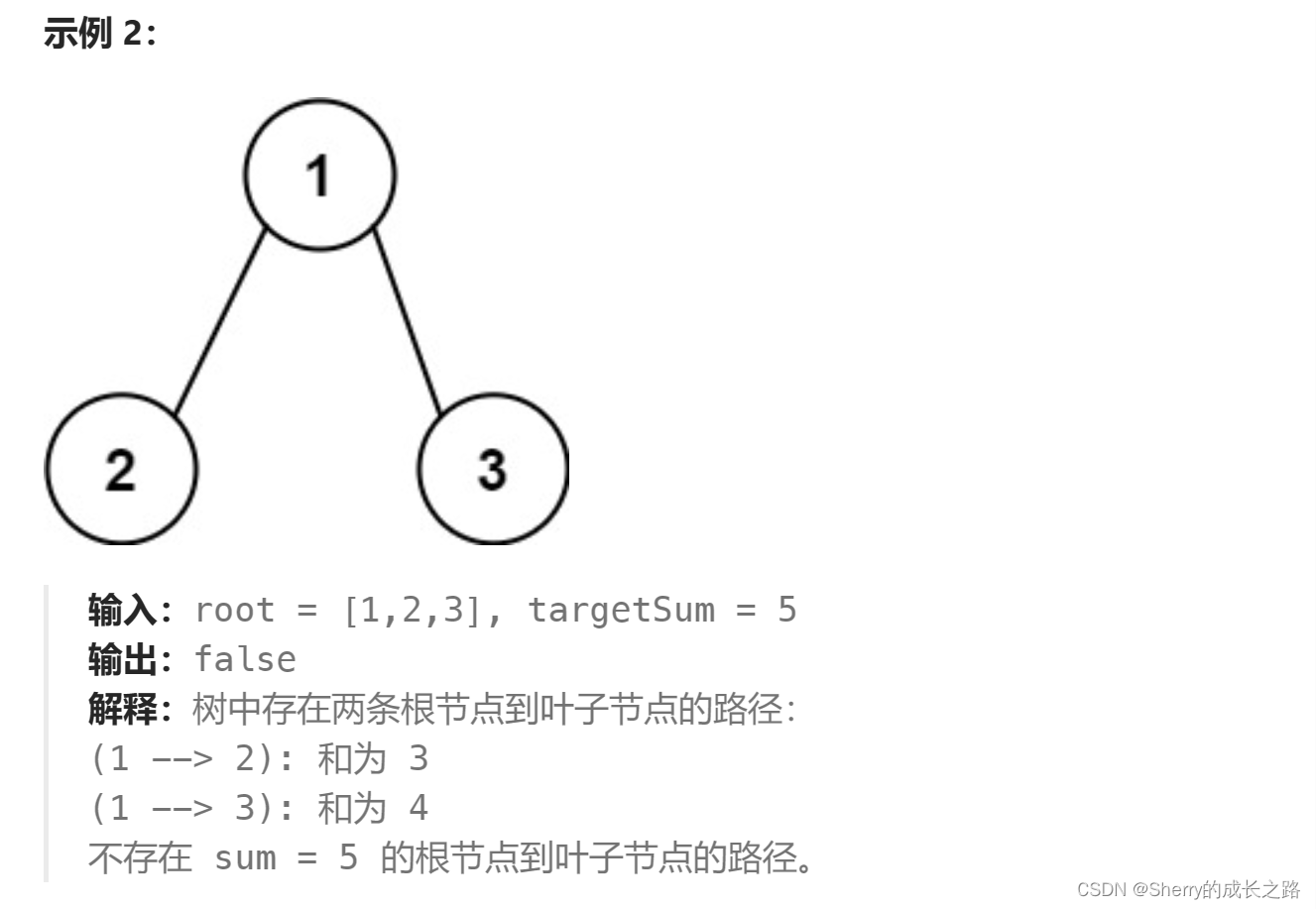
这道递归题是找到一个路径直接返回，所以我们需要注意，在单层递归逻辑中要处理当发现一条正确的路径后，如何将true向上层一次返回，尽快跳出循环，这是本题的关键所在。

class Solution {
public:
    bool traversal(TreeNode* cur,int count)
    {
        if(!cur->left&&!cur->right&&count==0)
        {
            return true;
        }
        if(!cur->left&&!cur->right)
        {
            return false;
        }
        if(cur->left)
        {
            count-=cur->left->val;
            if(traversal(cur->left,count))
            return true;
            count+=cur->left->val;
        }
        if(cur->right)
        {
            count-=cur->right->val;
            if(traversal(cur->right,count))
            return true;
            count+=cur->right->val;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr)
        {
            return false;
        }
        return traversal(root,targetSum-root->val);
    }
};

代码整体思路并不算难，用一个全局变量来保存该条路径总值等于多少，遍历到叶子节点我们做一次判断，如果总和等于目标值则向上返回true，这就是下面单层递归代码需要做的判断步骤，if上一层返回的是true，则继续向上返回直到跳出递归，这种思路在寻找一条正确答案就退出的题目来说，十分重要。

值得注意的是，我们在遍历到叶子节点时候，进入了递归的结束判断，不要忘记此时要在sum里加入当前叶子节点的值！这一点同样很重要，很容易就给落下，导致题目怎么做都是错误的，当然如果加入了还是false，那么在else里不要忘记将它减去（相当于回溯）。到全部都遍历完，如果还是不能返回true，那么直接返回false，表示无法找到。

这道题难的是递归的不同情况我们如何处理它们的返回，如果能搞得懂，那么还是可以做出来的。顺便说一句，如果在传入参数的时候传入的是目标值targetsum-头节点，再用传进来的目标值依次减去路径各节点判断到叶子节点时候是否等于0，那么在递归函数的结束判断代码部分会省一点力，当然递归部分代码目标值也要减去它下一个子树对应的val。

从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

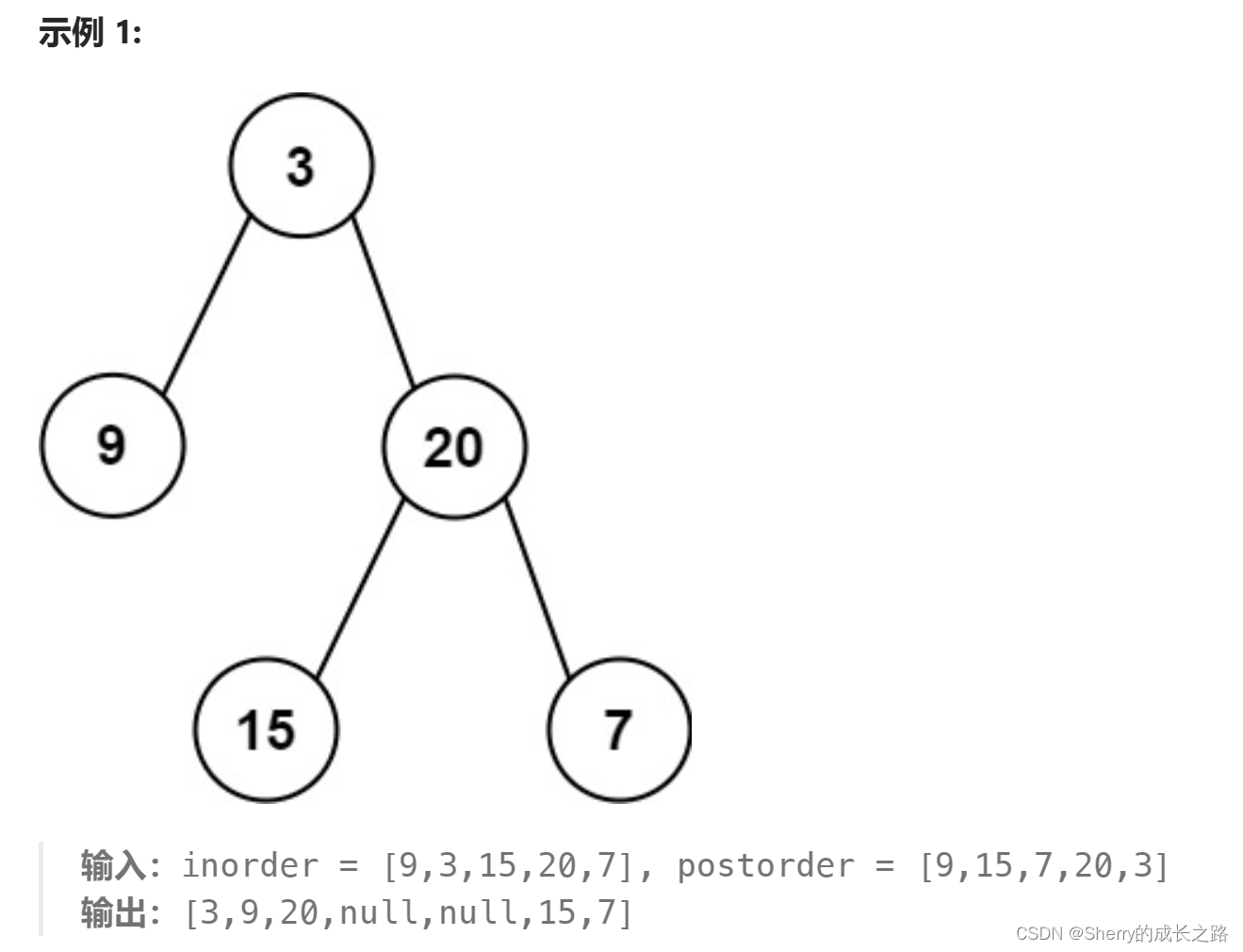
这道题是给一个中序遍历二叉树的数组和后序遍历二叉树的数组，用这两个数组，构造出来它实际想要表示的唯一的二叉树，并返回该二叉树的头部节点。

这道题的具体思路是：后序遍历的每次最后一个节点是每一个子树的中间节点。因为后序遍历左右中的遍历特点，它的最后一个节点首先应该是头部节点，也就是所谓的根节点，我们找到根节点了之后，在中序遍历数组中找到中节点所在的位置，将该数组分成左右两部分，左部分是左子树，右部分则是右子树所组成的节点，在做完这些的时候不要忘记将后序遍历的最后一个节点删除，以免重复进行数组的分割。

然后我们再进行后序数组的分割，我们之前已经说了后序数组是用来确定哪些节点此时应该做中节点的，我们按照中序数组左右部分的大小来切割后序数组，使它们能够左右部分一样大，然后在链接root->left和root->right时调用递归传进中序数组左部分（右部分）和后序数组左部分（右部分）即可。分为左右部分子树后，我们传进来的后续数组的部分就显得相当的重要了，他们的最后一个数据即是中间节点，重复以上步骤，直到节点全部插入，最重要的结束判断语句不要忘记，如果传进来的后序数组没有元素，则说明此时该侧子树节点全部安放完毕，不要漏掉这一步。主要是为了防止新节点存入没有必要的空指针，以及后来的遍历进入死循环，在全部递归完成return root即可。

class Solution {
public:
    TreeNode* traversal(vector<int>&inorder,vector<int>postorder)
    {
        if(postorder.size()==0)
        {
            return nullptr;
        }
        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue=postorder[postorder.size()-1];
        TreeNode* root=new TreeNode(rootValue);

        if(postorder.size()==1)
        {// 叶子节点
            return root;
        }
		// 找到中序遍历的切割点
        int delimiterIndex;
        for(delimiterIndex=0;delimiterIndex<inorder.size();delimiterIndex++)
        {
            if(inorder[delimiterIndex]==rootValue)
            {
                break;
            }
        }
        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInoder(inorder.begin(),inorder.begin()+delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInoder(inorder.begin()+delimiterIndex+1,inorder.end());
		// postorder 舍弃末尾元素
        postorder.resize(postorder.size()-1);
		// 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInoder.size());
        // [leftInorder.size(), end)
        vector<int> rightPostoder(postorder.begin()+leftInoder.size(),postorder.end());

        root->left=traversal(leftInoder,leftPostorder);
        root->right=traversal(rightInoder,rightPostoder);

        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0||postorder.size()==0)
        {
            return nullptr;
        }
        return traversal(inorder,postorder);

    }
};

总结：

今天我们完成了找树左下角的值、路径总和、从中序与后序遍历序列构造二叉树三道题，相关的思想需要多复习回顾。接下来，我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~