1、简述

        积分是微积分的一个主要部分。它是求和概念的延伸。事实上，积分符号源自一个拉长的字母S，最初由莱布尼茨使用（也有人说是牛顿），代表Summa，在拉丁语中意为“和”，对切片进行求和的想法。

        积分可用于查找面积、体积、中心点和许多有用的东西。但最好理解的简单的方法是从查找函数和 x 轴之间的面积开始，如下所示：

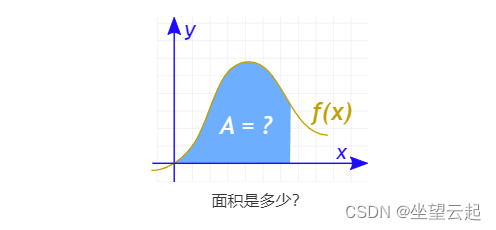
        我们可以在几个点计算函数并将宽度Δx的切片相加，如下图所示（但答案不会很准确）。

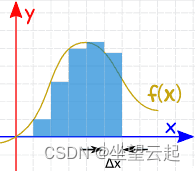
        但是我们可以使Δx变得更小，并 添加许多小切片（答案越来越接近）：  

        当切片宽度接近零时，答案就接近真实答案。我们现在写 dx表示Δx切片的宽度接近零。

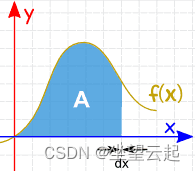
        如果熟悉求和符号，不熟悉可以参考下面的链接。

有趣的数学 求和符号Σ (sigma)简述_sigma求和符号-CSDN博客符号∑（sigma）通常用于表示多个项的总和。这个符号通常伴随着一个索引，该索引变化以包含总和中必须考虑的所有术语。例如，݊第一个整数的和可以用以下方式表示：或者，这两种表示意思都是一样的。更一般地说，表达式表示n项的总和。_sigma求和符号https://skydance.blog.csdn.net/article/details/131254446        然后得到黎曼和定义了曲线下的面积（定积分中还区分左黎曼和、右黎曼和、中点黎曼和、梯形法等等，这里提一下）

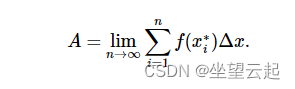
         于是人们定义定积分如下，积分符号闪亮登场。

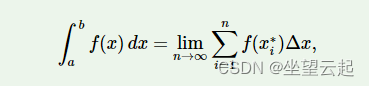
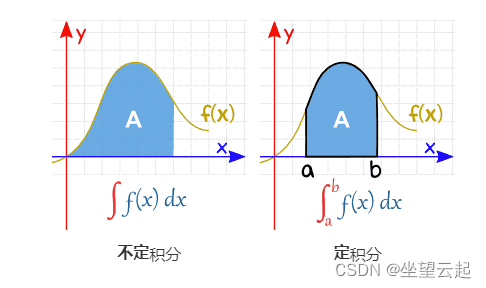
2、定积分

        积分符号有时在积分符号旁边有数字或其他字母。这些称为积分的极限，顶部的称为上限，底部的称为下限。 定积分具有要计算的实际值。

3、不定积分

        如果积分符号没有限制，则积分称为不定积分，这意味着没有特定值。相反，结果是一系列函数。积分以相同的方式执行，但我们必须记住添加一个称为积分常数的任意常数。

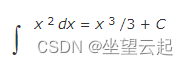
        一个更直观的图像