从零开始的Transformers第二篇:代码解析transformer架构

代码解析transformer架构

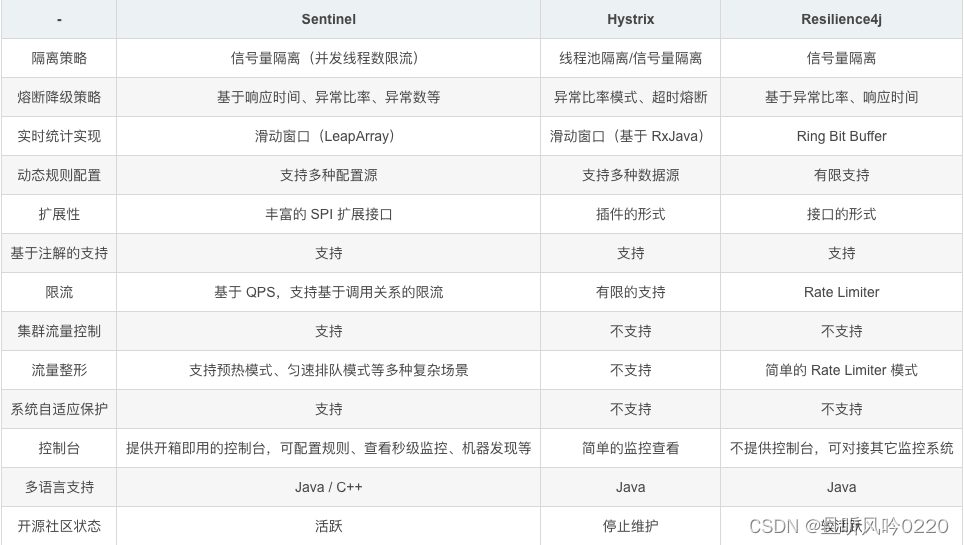
总体解析
输入部分
- 词向量
- Input Embedding
位置编码
编码器
- 自注意力机制
- 掩码
- 多头自注意力机制
- Feed Forward
- Layer Norm
- 残差链接
- Encoder Layer
解码器
输出头
总体模型
所有代码

总体解析

在这里插入图片描述

上面是 transformer 的论文中的架构图，从上面拆分各个模块的话，我们可以得到

Input Embedding : 对输入的词向量的表示方法进一步压缩其维度，使得其表示方法具备可学习性、压缩维度紧凑性等特点。
Positional Encoding ：使用正弦/余弦等位置编码方式，给不具备位置属性的编码之后的词向量加上位置编码。
Encode -> N 个 Encode Layer 组成：通过不断地对 Q、 K、V 进行自注意力操作，来提取文本中所蕴含的信息，最后输出提取到特征图给解码器使用。
Decode -> N 个 Decode Layer 组成：在掩码注意力层不断对已经输出的信息进行自注意力，获得蕴含的信息，再和编码器的输出做注意力，获得最终的输入输出文本中蕴含的信息。
Generator -> Linear Layer + Softmax Layer 组成：将输入和已经输出的信息压缩之后的信息，转化到合适的输出的维度，进行输出。

各个模块之间的任务是比较清楚的，通过大量的自注意力机制、注意力机制、掩码注意力机制，使得以文本输入或者以 “patch” 输入的的各个部分之间均有机会注意到 ”远端“ 那些 ”位置上不相关” 的信息，增加信息的 ”互动性“。

下面将详细的介绍各个模块的作用，并使用代码实现。

输入部分

Input Embedding : 对输入的词向量的表示方法进一步压缩其维度，使得其表示方法具备可学习性、压缩维度紧凑性等特点。

词向量

将字符串转化为计算机能够看懂的“数字形式”，如 ‘i’ 可以表示为 $[1, 0, 0]$ 或者就表示为 $1$ ，这样表示可以吗，可以的，但是：

$[1, 0, 0]$ 这样表示的话，有多少个词语，你向量的长度就为多少，想想我们世界上有那么多的词语，这个维度就很恐怖，再想想还要做注意力计算，就更恐怖了。其次是 $[1, 0, 0]$ 一种绝对的硬编码，忽略了相近词语之间的“相似性”。
$1$ 这样表示虽然没有了维度上的灾难，但是使用 $1....100.... N$ 这样表示词语，词语感觉好像具备了 “大小”。这样容易使得网络 “带歪”。

上述的办法虽然具备缺点，但是还是具备可行性的。如果我们采用 $[1, 0, 0]$ + $N$ 的方式，是不是即解决了 $[1, 0, 0]$ 的稀疏性，又解决了 $N$ 大小性。把词向量变成 $[0.8, 0.11, 0.09]$ ，这样的话，是不是合理起来了。

但实际上有个问题，你怎么知道 ’i’ 的词向量应该为 $[0.8, 0.11, 0.09]$ ? 那么多的词语，我们该怎么获得他们的词向量呢？再说吗，即便我们设定对应的稠密词向量，网络认不认？网络想要的是不是我们设定的这种呢？既然我们设定麻烦且不合适，那让网络自己去设定。

Input Embedding

Input Embedding 层就是这样干的。假设我们输入原始稀疏词向量为 10000 维的，我们想要将其压缩，变成 512 维的稠密的。我们是不是可以加上一个变换矩阵就可以了。公式如下：
$Y = W * X 或者 Y = W^T * X$
表示形式大差不差，只要 $W$ 为 $10000 * 512$ 的，或者 $512 * 10000$ ，看你设定。因为 $W$ 在网络中，是可以训练的，这样网路需要什么， $W$ 就是什么。

下面是代码实现：
头文件

import torch.nn as nn

class Embedding(nn.Module):
    def __init__(self, d_vocab, d_model):
        super().__init__()
        self.d_model = d_model
        # 直接调用的 torch 里面存在好的模块
        self.emb = nn.Embedding(d_vocab, d_model)
    
    def forward(self, x):
        # 其中 math.sqrt(self.d_model) 为缩放因子 
        return self.emb(x) * math.sqrt(self.d_model)

测试代码。


if __name__ == "__main__":
    d_model = 512
    d_vocab = 1024
    x = Variable(torch.LongTensor([[100, 2, 421, 50], [300, 60, 2, 19]]))
    emb = Embedding(d_vocab, d_model)
    embx = emb(x)
    # 原本是 onehot 的话， embx.size() == (2, 4, max(x))
    # 现在是 [2, 4, 512]， 所以 nn.Embedding == W == onehot(x) * [(max(x), d_model])
    # 将原本稀疏的变量变成稠密变量，和 word2vec 是一个样子，将 num_embeddings 理解为onehot 维度，也就是
    # 词向量的个数
    print("embr : ", embx.size())

位置编码

为什么需要位置编码呢？解析一下：
简单来说，”you love china“ 和 ”china love you“，”you“ 在这两个短句中的意思是不一样的，但如是我们采用自注意力的话，”you“ 在获得的注意力的结果是一样的(因为都是和 ”love“ 和 ”china“ 做自注意力)，那这样就没区别了。那不行，需要你有区别，位置编码闪亮产生。
位置编码一般有两种方式：

采用稀疏的位置向量表示。 $[1, 0, 0]$ 表示位置0， $[0, 1, 0]$ 表示位置1，将这种稀疏表示加到编码过的稠密词向量中即可。
采用余弦/正弦的方式，具体公示如下：
$\begin{aligned} P E_{(p o s, 2 i)} & =\sin \left(\text { pos } / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)} & =\cos \left(\text { pos } / 10000^{2 i / d_{\text {model }}}\right) \end{aligned}$

公式看上去可能有点麻烦，其实很简单。
其中 $p os$ 代表词在句子中的位置，2i 代表词向量中的位置。假设句子 ”I love you“中 ‘I’ 的 pos 为 0，词向量的维度为 512 -> $[0, .... n .., 511]$ 。
我们在 n = 2i 也就是偶数的时候，采用 $E_{(0, n)} = \sin \left(\text { 0 } / 10000^{ n / d_{\text {model }}}\right) = 0$
我们在 n = 2i + 1 的时候，采用 $E_{(0, n)} =\cos \left(\text { 0 } / 10000^{n - 1 / d_{\text {model }}}\right) = 1$

上面的公式次幂是比较的，我们可以加以简化，看起来更清楚。
$\begin{aligned} 1 / 10000^{2 i / d_{\text {model }}} = exp(log^{(1 / 10000^{2 i / d_{\text {model }}})}) \\ = exp({2i/d_{\text {model }}} * log^{10000^{-1}}) =exp^{(2i/ d_{\text {model }} * (- log10000))} \end{aligned}$
简化之后，防止出现10000幂次的计算，实现代码也一般采用这种方式。下面将使用代码实现这种方式。
我们也可以看到，无论是 $cos$ 还是 $s in$ ，计算位置编码的时候，我们只需要计算 2i 位置上的 $exp^{(2i/ d_{\text {model }} * (- log10000))}$ ，所以计算量也少了一半。
下面是代码的实现。

import math
import torch
import torch.nn as nn
from torch.autograd import Variable

import numpy as np
from matplotlib import pyplot as plt

class PositionEmbedding(nn.Module):
    def __init__(self, d_model=512, p_dropout=0.1, max_len=5000):
        super().__init__()
        # 对输入进行随即丢弃
        self.dropout = nn.Dropout(p=p_dropout)
        
        # 先初始化一个全为 0 的位置编码
        pe = torch.zeros((max_len, d_model))
        position = torch.arange(0, max_len).unsqueeze(1) # => (max_len, 1)
        # 进行正弦和余弦的位置编码
        # pe(pos, 2i)     = sin(pos/10000^(2i/d_model)) = sin(pos * e^(2i * -log(10000.0)/ d_model ))
        # pe(pos, 2i + 1) = cos(pos/10000^(2i/d_model)) = cos(pos * e^(2i * -log(10000.0) / d_model ))
        # 怎么理解 pos 和 i， ==》 pos 代表第输入中单词在pos位置， 而 i 代表词向量中的位置
        # torch.arange(0, d_model, 2) 对应 2i
        div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        
        # 此时 pe = (max_len, d_model)，因为我们的输入为三维，带有 batch_size
        pe = pe.unsqueeze(0)
        
        # 最后将 pe 注册为模型的 buffer，什么是 buffer 呢？
        # 我们把它认为是对模型有帮助的,但是却不是模型中的超参数,不需要随着优化步骤进行更新增益对象
        # 注册之后,我们就可以在模型保存后重加载时和模型结构参数一同被记载,
        # 可以被认为是绑定到我们的模型的一些不优化的参数 -> state_dict() 中
        # 解释 : https://blog.csdn.net/weixin_46197934/article/details/119518497
        self.register_buffer('pe', pe)
    def forward(self, x):
        # 将当前输入的[batch, word_len, d_model] + pe
        # 为什么 :x.size(1),因为我们提前算好 max_len,方便一点
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)

为了更好的理解位置编码，我们采用可视化的方式，将这种位置编码可视化出来。代码如下：

if __name__ == "__main__":
# 绘制位置编码
	# d_model = 512 绘制的图太密集了，这里改为 20 理解一下就行。
    pe = PositionEmbedding(d_model=20)
    # squeeze 的原因是因为我们在类中对位置编码添加了 batch 的维度，这里拿出来
    y = pe.squeeze(0).numpy()
    
    plt.figure(figsize=(20, 10))
    # 显示 d_model 的随着 d_model 的不同的直的变化范围
    plt.plot(np.arange(20), y[0, :])
    # 绘制相同位置的i在不同的单词位置的上的变化范围
    plt.plot(np.arange(100), y[:100, 4:8])
    plt.legend(["word site", *["dim %d" % p for p in [4, 5, 6, 7]]])
    # plt.savefig("./位置编码显示.png")
    plt.show()

结果如下：
在这里插入图片描述
也可以比较以下加入了位置编码和没有加入位置编码区别：
代码如下：

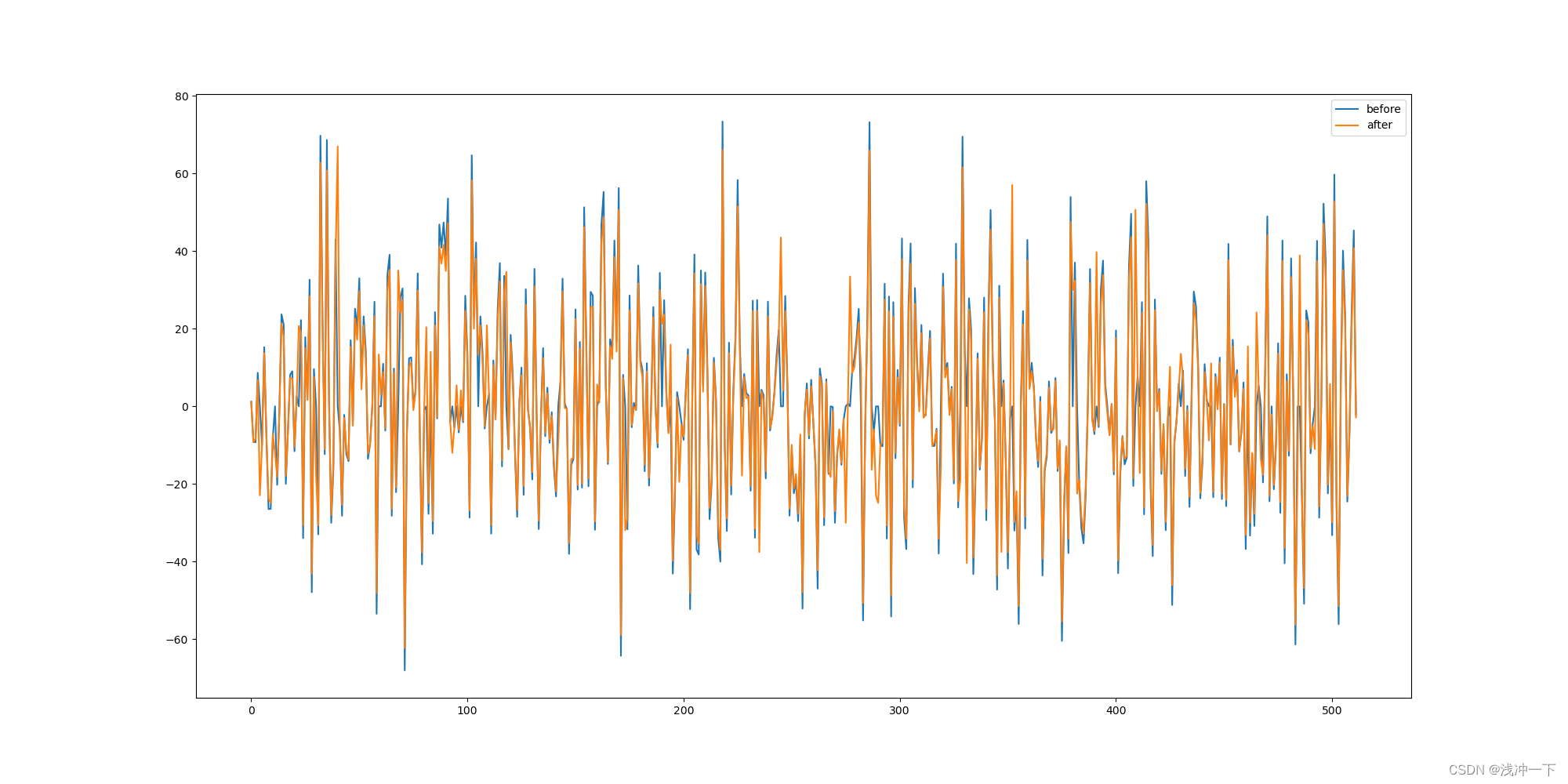
if __name__ == "__main__":
	x = Variable(torch.LongTensor([[100, 2, 421, 50]]))
    emb = Embedding(d_model=512, d_vocab=1024)
    pe = PositionEmbedding(d_model=512)
    embx = emb(x)
    np_embx = embx[0][0].detach().numpy()
    pe_embx = pe(embx)
    
    np_pe_embx = pe_embx[0][0].detach().numpy()
    
    plt.figure(figsize=(20, 10))
    # 显示 d_model 的随着 d_model 的不同的直的变化范围
    # plt.plot(np.arange(20), pe_embx[0, :])
    # 绘制相同位置的i在不同的单词位置的上的变化范围
    plt.plot(np.arange(512), np_pe_embx[:])
    plt.plot(np.arange(512), np_embx[:])
    plt.legend(["%s" % s for s in ["before", "after"]])
    plt.show()

固定单个 $p os$ ，看 $i$ 的影响，结果如下：
在这里插入图片描述
看 $p os$ 从 0 变成 100 对词向量的影响如下：

if __name__ == "__main__":
    x = Variable(torch.LongTensor([[100, 2, 421, 50] * 100]))
    emb = Embedding(d_model=512, d_vocab=1024)
    pe = PositionEmbedding(d_model=512)
    embx = emb(x)
    np_embx = embx[0][0].detach().numpy()
    pe_embx = pe(embx)
    
    np_pe_embx0 = pe_embx[0][0].detach().numpy()
    np_pe_embx100 = pe_embx[0][99].detach().numpy()
    
    plt.figure(figsize=(20, 10))
    # 显示 d_model 的随着 d_model 的不同的直的变化范围
    # plt.plot(np.arange(20), pe_embx[0, :])
    # 绘制相同位置的i在不同的单词位置的上的变化范围
    plt.plot(np.arange(512), np_embx[:])
    plt.plot(np.arange(512), np_pe_embx0[:])
    plt.plot(np.arange(512), np_pe_embx100[:])
    plt.legend(["%s" % s for s in ["before", "after pos = 0", "after pos = 100"]])
    plt.savefig("./位置编码显示.png")
    plt.show()

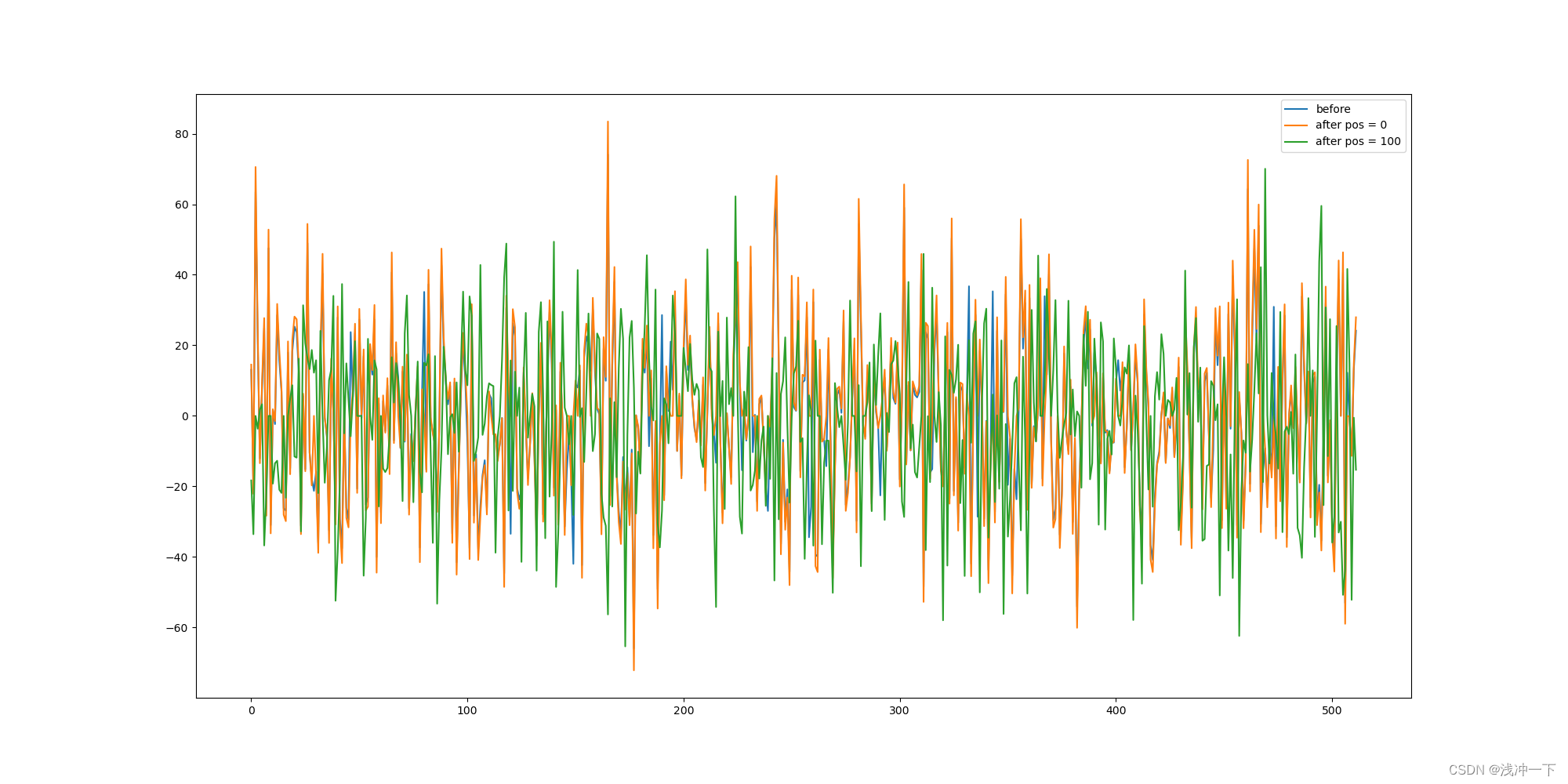
在这里插入图片描述
看的出来，加入位置编码之后，相同的词向量发生了比较大变化，也代表着我们加入的位置编码起了作用。

编码器

要想聊编码器和解码器，需要先聊一下自注意力机制和多头自注意力机制

自注意力机制

关于注意力的公式，这里采用 tansformer 文中的公式
$\operatorname{Attention}(Q, K,V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V$
关于其他采用 $co n c a t$ 和 $so f t ma x$ 结合的注意力公式，这里不再赘述。
注意力如图示所示：
在这里插入图片描述

关于注意力和自注意力的区别，这里简述如下：

注意力： $Q == K == V$ 。
自注意力： $Q == K == V$ 。

根据上面公式理解如下，使用已知的 $Q$ 先和关键词 $K$ ，进行计算，得到了得分，这个时候，从 $V$ 中以 $Q K^{T}$ 结果为得分权重从 $V$ 中拿出对应的值。自不自注意力的，关键看 $Q$ 有没有带来外界新的信息进行交互。
代码实现如下：

import math
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np
from matplotlib import pyplot as plt
from copy import deepcopy as c

def attention(query, key, value, mask=None, dropout=None):
    """
    计算公式为： ans = softmax(Q * K_T / sqrt(d_k)) * V
    """
    # 计算注意力机制的分数
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)

    # 是否存在掩码张量
    if mask is not None:
        # 将 mask 为 0 的地方设置为 -1e9
        scores = scores.masked_fill(mask == 0, -1e9)

    # 计算 softmax
    p_attn = F.softmax(scores, dim=-1)
    
    # 是否存在 dropout
    if dropout is not None:
        p_attn = dropout(p_attn)
    
    # 返回注意力机制的值和注意力机制的分数, 并返回注意力机制的值
    return torch.matmul(p_attn, value), p_attn

测试代码如下：

if __name__ == "__main__":
    # 测试注意力机制
    x = Variable(torch.LongTensor([[1, 2, 3, 4], [4, 13, 2, 1]]))
    emb_x = Embedding(d_model, 1024)(x)
    pe_emb_x = PositionEmbedding(d_model)(emb_x)
    
    query = key = value = pe_emb_x
    socres, attn = attention(query, key, value)
    print(socres.size(), attn.size())

掩码

上面的代码中，我们使用一个mask，在 encoder 中一般为None。一般被使用在 decoder 中。主要是防止网络提前看到最终输出的信息。
为什么会看到最终输出的信息呢？
因为我们在训练网路的时候，会一次性将最终的所有预测的答案送给网络。便与并行计算和计算损失函数。
但是这样的话，做自注意力机制的时候，网络还没有输出的部分就会被网络计算注意力的时候计算到，这样不是我们想看到的，于是乎我们想要网络已经输出的部分才能被看到，其他剩余部分不能被看到。
代码和图示如下：

def subsequent_mask(size=512):
    """
    生成向后的掩盖的掩码张量， 参数 size 是掩码张量的最后两个维度的大小，
    它的最后两维形成一个方阵
    1 0 0 0
    1 1 0 0
    1 1 1 0
    1 1 1 1
    可以理解为前面的输入没必要和后面还没有输入的地方做注意力机制，
    """
    # 先形成全1矩阵，再变换为上三角矩阵，最后1减去就变成了下三角矩阵了
    subsequent_mask = np.triu(np.ones((1, size, size)), k = 1).astype(np.int8)
    return torch.from_numpy(1 - subsequent_mask)

也可以画图展示如下：

if __name__ == "__main__":
    x = subsequent_mask(size=20)
    plt.figure(figsize=(6, 6))
    plt.imshow(x[0])
    # print(x)
    plt.show()

在这里插入图片描述

多头自注意力机制

聊完自注意力机制，还需要聊一下多头自注意力机制：
在这里插入图片描述

先说原因：在多个子空间里计算一方面可以降低计算量，另一方面可以增加特征表达的性能
假设 8 个头。 $d_{model} = 512$ ，则每个头 64 维的词向量。
1、可以降低计算量：
一个头时候的计算量为 n * 512 * 512 * n * n * 512 -> 八个头的时候的计算量 n * 64 * 64 * n * n * 64 * 8
计算量是减少了一些。
2、增加特征表达的性能
一个头中的注意力可能会一直偏执向某个方向，这个方向，万一出现错误，整个注意力将很难偏执回来。多个头有多种捕捉信息的能力。
$\operatorname{MutilHeadAttention}(Q, K,V)=\operatorname{concat(\operatorname{softmax}\left(\frac{Q^h K^{hT}}{\sqrt{d_{k}^h}}\right) V^h)} \\ 其中 {(Q, K, V)}^h 表示原始 Q,K,V 的同位置 h 分之一$

代码如下：

import math
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np
from matplotlib import pyplot as plt
from copy import deepcopy as c

def clone_modules(module, N):
    """
    克隆 N 个 module
    """
    return nn.ModuleList([c(module) for _ in range(N)])

class MultiHeadedAttention(nn.Module):
    """
    实现多头注意力机制
    """
    def __init__(self, head=8, embedding_dim=512, p_dropout=0.1):
        super().__init__()
        #  确定多头的head需要整除词嵌入的维度
        assert embedding_dim % head == 0
        
        # 确认每个头的词嵌入的维度
        self.d_k = embedding_dim // head
        self.head = head
        self.embedding_dim = embedding_dim
        
        # 获得线性层， 需要获得4个，分别是 Q、K、V 和最后的输出
        self.linears = clone_modules(nn.Linear(embedding_dim, embedding_dim), 4)
        
        # 初始化注意力张量
        self.attn = None
        
        # 初始化 dropout 对象
        self.dropout = nn.Dropout(p=p_dropout)
    
    def forward(self, query, key, value, mask=None):
        # 是否存在 mask 
        if mask is not None:
            # 因为是多头注意力机制，所以这里需要将 mask 扩展维度
            mask = mask.unsqueeze(0)
            
        # 接着，我们获得一个batch_size的变量， 代表有多少条样本
        batch_size = query.size(0)
        
        # view 是为了让 Q、K、V变成多头注意力的形式， 但是这样的形式，是没有办法输入到attention 中
        # 进行并行处理的， 如果把 head 和 词数量 的位置变化一下，就是每个头单独进行注意力计算
        query, key, value = \
            [model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
             for model, x in zip(self.linears, (query, key, value))]
        
        # 将多个头的输出送入到 attention 中一起并行计算注意力即可
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
        
        # 得到多头注意力的结果之后，我们还需要转化一下维度，拼凑为原始的 d_model 的注意力机制
        x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.embedding_dim)
        
        # 最后输出的时候，再经过一个线性变换层即可
        return self.linears[-1](x)

测试代码如下：

if __name__ == "__main__":
    head = 8
    d_model = 512
    p_dropout = 0.1
    
    # 测试注意力机制
    x = Variable(torch.LongTensor([[1, 2, 3, 4], [4, 13, 2, 1]]))
    emb_x = Embedding(d_model, 1024)(x)
    pe_emb_x = PositionEmbedding(d_model)(emb_x)
    query = key = value = pe_emb_x
	mask = subsequent_mask(size=4)
	# 测试多头注意力机制
    mha = MultiHeadedAttention(head, d_model, p_dropout)
    mha_result = mha(query, key, value, mask)
    print("mha_result :", mha_result.size())

Feed Forward

为了增强网络的提取能力和非线性能力，transformer 引入了一个 两层全连接线性层，来增加网络的能力。如下图红色框中所示：
在这里插入图片描述
代码实现如下;

class PositionwiseFeedForward(nn.Module):
    """
    前馈全连接层，d_ff 为隐藏层单元数量
    return linear(dropout(relu(linear(x))))
    """
    def __init__(self, d_model, d_ff, p_dropout=0.1):
        super().__init__()
        self.f1 = nn.Linear(d_model, d_ff)
        self.f2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(p=p_dropout)
        
    def forward(self, x):
        return self.f2(self.dropout(F.relu(self.f1(x))))

测试代码如下：

if __name__ == "__main__":
    head = 8
    d_model = 512
    p_dropout = 0.1
    
    # 测试注意力机制
    x = Variable(torch.LongTensor([[1, 2, 3, 4], [4, 13, 2, 1]]))
    emb_x = Embedding(d_model, 1024)(x)
    pe_emb_x = PositionEmbedding(d_model)(emb_x)
    query = key = value = pe_emb_x
    mask = subsequent_mask(size=4)
    
    # 测试多头注意力机制
    mha = MultiHeadedAttention(head, d_model, p_dropout)
    mha_result = mha(query, key, value, mask)
    print("mha_result :", mha_result.size())
    
    # 测试前馈全连接层
    ff = PositionwiseFeedForward(d_model, 64, p_dropout)
    ff_result = ff(mha_result)
    print("ff result size : ", ff_result.size())

Layer Norm

我们可以注意到。无论是多头注意都存在一个 Layer Norm，
在这里插入图片描述

其主要作用是在 batch * num_word * d_model 的中 d_model 的维度上进行归一化操作。防止网络经过多层之后，网络权值出现漂移发散等问题。

也就是使用训练所得的均值和方差替换掉原有的均值和方差。

代码如下：

class LayerNorm(nn.Module):
    """
    对单个batch、单个样本中的最后特征维度进行归一化操作，
    解决NLP中 BN 中输入样本长度不一致的问题
    """
    def __init__(self, features_size, eps=1e-6):
        super().__init__()
        self.train_mean = nn.Parameter(torch.ones(features_size))
        self.train_std = nn.Parameter(torch.zeros(features_size))
        self.eps = eps
    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return (x - mean) / (std + self.eps) * self.train_mean + self.train_std

残差链接

根据网络架构来说，我们每一个 block 的输出和输出之间还要进行一个残差链接，可以缓解网路深度所带来的过拟合和权值更新过慢的问题。在这里插入图片描述

代码如下：

class SublayerConnection(nn.Module):
    """
    对照着模型进行残差连接
    """
    def __init__(self, size, p_dropout=0.1):
        super().__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(p=p_dropout)
        
    def forward(self, x, sublayer):
        # 在论文复现的时候发现 self.norm 放在 里面 比放在 外面 好
        return x + self.dropout(sublayer(self.norm(x)))

Encoder Layer

Encoder 是由一层一层的下图所示的结构所构成，所以我们需要先将 MultiHeadedAttention 、PositionwiseFeedForward、LayerNorm、SublayerConnection进行组成成一个大的层。组装代码如下：
在这里插入图片描述

class EncoderLayer(nn.Module):
    def __init__(self, d_model, attn_layer, feed_forward_layer, dropout):
        super().__init__()
        self.d_model = d_model
        self.attn = attn_layer
        self.feed_forward = feed_forward_layer
        
        # 还需要初始化两个残差连接
        self.subLayers = clone_modules(SublayerConnection(d_model, dropout), 2)
        
    def forward(self, x, mask):
        # 经过多头注意力层，然后残差，然后前馈层，然后再残差
        x = self.subLayers[0](x, lambda x : self.attn(x, x, x, mask))
        return self.subLayers[1](x, self.feed_forward)

最后N 个 Encoder Layer 组装以下可以形成我们的 Encoder 了。
代码如下

class Encoder(nn.Module):
    def __init__(self, layer, N):
        super().__init__()
        self.norm = LayerNorm(layer.d_model)
        self.layers = clone_modules(layer, N)
        
    def forward(self, x, mask):
        for layer in self.layers:
            x = layer(x, mask)
        return  self.norm(x)

解码器

由于我们在上面讲完了MultiHeadedAttention、PositionwiseFeedForward、LayerNorm、 SublayerConnection。再对比 encoder 的图示，我们再聊一下其中的注意力层就欧克了。
在这里插入图片描述
我们可以注意到，decoder layer，先经过一个自注意力机制，然后需要从和 encoder 出来的压缩的信息进行注意力机制，所以说此时的Q != K == V。多传入一个encoder的输出即可。代码如下;

class DecoderLayer(nn.Module):
    def __init__(self, d_model, self_attn, src_attn, feed_forward, p_dropout) -> None:
        super().__init__()
        # self_attn 为自注意力机制 src_attn 为原始的多头注意力机制
        self.d_model = d_model
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.ff = feed_forward
        self.subLayers = clone_modules(SublayerConnection(d_model, p_dropout), 3)
        
    def forward(self, x, m, src_mask, tgt_mask):
        """
        x: 上一层的输入， m(memory): 来自编码器的输出， src_mask: 原数据掩码，tgt_mask: 目标数据掩码
        """
        # 第一步，是解码器的输入自己和自己作注意力机制，这个时候哦，我们不希望前面已经输出的和后面的词作注意力机制
        # 因为解码器端口的输入是我们一次给完整的，方便我们计算损失和并行化
        x = self.subLayers[0](x, lambda x : self.self_attn(x, x, x, tgt_mask))
        # 第二步：是解码器输入得到的注意力结果之后，和我们编码器的最终的输出进行注意力的操作，
        # 这里的 src_mask 并不是因为抑制信息泄漏，而是屏蔽对结果没有意义的字符而产生的注意力的值，以此提升模型效果和训练速度（输入中无用的字符？）
        x = self.subLayers[1](x, lambda x : self.self_attn(x, m, m, src_mask))
        
        return self.subLayers[2](x, self.ff)
        
class Decoder(nn.Module):
    def  __init__(self, layer, N):
        super().__init__()
        self.norm = LayerNorm(layer.d_model)
        self.layers = clone_modules(layer, N)
        
    def forward(self, x, m, tgt_mask, src_mask):
        for layer in self.layers:
            x = layer(x, m, tgt_mask, src_mask)
            
        return self.norm(x)

输出头

在这里插入图片描述
输出头的结构比较简单，主要承担的是维度变化和最终概率的输出。

class Generator(nn.Module):
    def __init__(self, d_model, vocab_size) -> None:
        super().__init__()
        self.project = nn.Linear(d_model, vocab_size)
        
    def forward(self, x):
        # log_softmax 和 softmax 对于最终的输出是没有影响的，
        # 但是可以解决 softmax 数值不稳定的现象
        return F.log_softmax(self.project(x), -1)

总体模型

class EncoderDecoder(nn.Module):
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator
    
    def forward(self, src, tgt, src_mask, tgt_mask):
        return self.generator(
                self.decode(
                    self.encode(src, src_mask), src_mask, tgt, tgt_mask))
    
    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)
    
    def decode(self, m, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), m, src_mask, tgt_mask)
    
# 构建用于 transformer 的模型
def make_model(src_vocab, tgt_vocab, N=6, 
                d_model=512, d_ff=2048, head=8, p_dropout=0.1):
    # 初始化一些需要公用的层,后面使用deepcopy,
    attn = MultiHeadedAttention(head, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, p_dropout)
    pos_layer = PositionEmbedding(d_model, p_dropout)
    
    # 初始化我们的模型
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), p_dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), p_dropout), N),
        nn.Sequential(Embedding(d_model, src_vocab), c(pos_layer)),
        nn.Sequential(Embedding(d_model, src_vocab), c(pos_layer)),
        Generator(d_model, tgt_vocab)
    )
    
    # 初始化那些参数维度大于一的，将其初始化为服从均匀分布的矩阵。显示的设置模型参数
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform(p)
    
    return model

最后打印测试一下模型如下：

if __name__ == "__main__":
    src_vocab = 100
    tgt_vocab = 100
    N = 6
    
    x = Variable(torch.LongTensor([[1, 2, 3, 4], [4, 13, 2, 1]]))
    decode_mask = subsequent_mask(4)
    transformer = make_model(src_vocab, tgt_vocab, N)
    print(transformer(x, x, decode_mask, decode_mask).size())
    torch.onnx.export(transformer, (x, x, decode_mask, decode_mask), "temp.onnx")