双指针,顾名思义就是指针的指针。
在此之前我们需要先理解单指针 (简称为指针)。指针很简单,直接上例子:例:现有两个变量,a=10,b=20.
要求:交换他们的值,输出的结果应为a=20,b=10。
#include <bits/stdc++.h>
using namespace std;
void swap(int a, int b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int a = 10, b = 20;
swap(a, b);
cout << a << " " << b << endl;
return 0;
}
乍一看没问题,结果:
交换失败。失败的原因是在函数swap(int a,int b)中,接收的a和b是两个整型的值而不是指针(换句话说,这里交换的是形式参数而非实际参数)。int a=10;int b=10;定义的是两个实际参数,swap(int a,int b)中的a和b是形式参数,形参的交换对实参的交换是没有影响的。因此要将void swap(int a, int b)修改为void swap(int &a, int &b)
#include <bits/stdc++.h>
using namespace std;
void swap(int &a, int &b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int a = 10;
int b = 20;
swap(a, b);
cout << a << " " << b << endl;
return 0;
}
成功。这里的void swap(int &a, int &b)是引用传递,当你调用这个函数时交换操作会直接修改变量a和b的值。这意味着函数外部的变量a和b的值也会发生交换。
当你使用swap(int *a, int *b)函数时得出的结果和上述的引用传参是一样的,但是原理不同:此时参数a和b是指向整型的指针,函数内部通过指针操作来交换变量的值。
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
它们的运行结果相同。总结:引用方式和指针方式的交换两个变量的值的区别:
1、语法:
引用方式:使用引用作为形式参数,在函数内部直接操作引用所绑定的变量。
指针方式:使用指针作为形式参数,在函数内部通过引用指针所指向的地址来修改变量的值。因此引用方式的执行效率更高。
2、调用方式:
引用方式直接将变量作为实际参数传递给函数,无需取地址操作。
指针方式:将变量的地址作为实际参数传递给函数,在调用时取地址操作符&。
3、影响范围:
引用方式通过引用传递,函数内部的修改会直接影响到函数外部的变量。
指针方式:通过指针传递,函数内部的修改只影响指针所指向的内存地址,不会修改指针外部的变量。注意:在函数内部修改指针指向的值,则会影响函数外部的变量。
4、错误处理:
**引用方式的引用必须绑定到一个已存在的对象,**所以在使用引用方式交换值时不需要考虑空指针或者野指针的可能性。
指针方式:指针可以为NULL或者指向未知的内存地址,所以在使用指针交换值时需要注意指针的有效性,避免空指针或者野指针的访问。
因此:我们明白了:引用方式更为简洁和安全;指针方式更加灵活,可以处理更多的特殊情况,但是相对复杂。
接下来就可以开始介绍:双指针
#include <bits/stdc++.h>
using namespace std;
void swap(int **a, int **b) {
int *temp = *a;
*a = *b;
*b = temp;
}
int main() {
int a = 10;
int b = 20;
int *str1 = &a;
int *str2 = &b;
swap(&str1, &str2);
cout << *str1 << " " << *str2 << endl;
return 0;
}
和单指针对比着看就很直观了!swap的形式参数的a和b各多了一颗“*”,整型变量temp多了一颗*。其余的没有变化。因此双指针就是给指针又套上了一个指针,并没有很复杂。学完了双指针,我们来做一题对应的习题:LeetCode102 二叉树的层次遍历
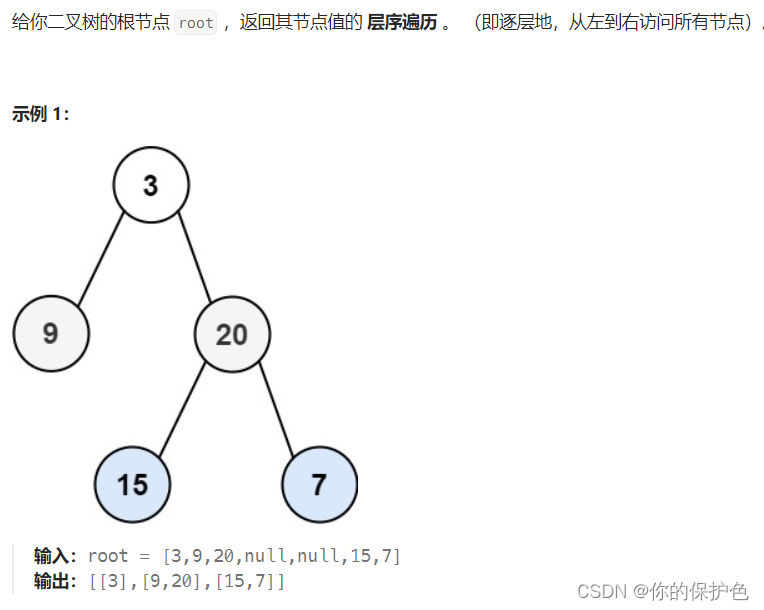
核心代码:
int **levealOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes) { //层序遍历函数
int **ans = (int **)malloc(sizeof(int *) * 2000); //动态创建一个二维数组ans用于存储层序遍历的结果
*returnSize = 0; //所在层数
if (!root)
return NULL;
int columnSizes[2000];//存所在层的结点
struct TreeNode *queue[2000];//用于存储结点的队列
int rear = 0, head = 0; //表示队头和队尾的索引
queue[rear++] = root; //将结点进入队列
while (rear != head) {
ans[(*returnSize)] = (int *)malloc(sizeof(int) * (rear - head)); //存储当前结点
columnSizes[(*returnSize)] = rear - head; //存储当前层的结点数量
int start = head; //当前层在队列中的起始位置
head = rear; //头部索引变为尾部索引,表示将要开始遍历下一层
for (int i = start; i < head; i++) { //遍历当前层的所有结点
ans[(*returnSize)][i - start] = queue[i]->val;
if (queue[i]->left)
queue[rear++] = queue[i]->left;
if (queue[i]->right)
queue[rear++] = queue[i]->right;
}
(*returnSize)++;
}
*returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize));
for (int i = 0; i < *returnSize; i++)
(*returnColumnSizes)[i] = columnSizes[i];
return ans;
}
该算法是一个层序遍历算法.层序遍历的过程用大白话描述就是:
if 无根结点,结束
else 有根结点
(1)先遍历根结点;
(2)若有左孩子,将左结点放入队列数组中;
(3)若有右孩子,将右结点放入队列数组中;
重复上述过程直到结点为NULL。
关于这个算法核心部分的解释:首先levealOrder函数的形式参数有3个,第一个是单指针指向(或者说引用)根结点root,
第二个是单指针指向层序遍历的初始层数,
第三个是双指针指向每层结点数量的数组。
该函数最终要返回一个存储层序遍历结果的二维数组ans[][].
int **ans指向一个动态创建的二维数组,用于存储层序遍历的结果:
行代表所在层,列代表所在层的结点位置。即ans[returnSize][rear-head].
(rear-head)是当前层的结点的位置。head和rear分别是队头和队尾的索引。
queue[]用于存储结点以方便遍历。
columnSize用于存储每层结点的数量;
完整代码:
#include <bits/stdc++.h>
using namespace std;
typedef struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
TreeNode *createNode(int val) {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode ->val = val;
newNode ->left = NULL;
newNode ->right = NULL;
return newNode;
}
int **levealOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes) { //层序遍历函数
int **ans = (int **)malloc(sizeof(int *) * 2000); //动态创建一个二维数组ans用于存储层序遍历的结果
*returnSize = 0; //所在层数
if (!root)
return NULL;
int columnSizes[2000];//存所在层的结点
struct TreeNode *queue[2000];//用于存储结点的队列
int rear = 0, head = 0; //表示队头和队尾的索引
queue[rear++] = root; //将结点进入队列
while (rear != head) {
ans[(*returnSize)] = (int *)malloc(sizeof(int) * (rear - head)); //存储当前结点
columnSizes[(*returnSize)] = rear - head; //存储当前层的结点数量
int start = head; //当前层在队列中的起始位置
head = rear; //头部索引变为尾部索引,表示将要开始遍历下一层
for (int i = start; i < head; i++) { //遍历当前层的所有结点
ans[(*returnSize)][i - start] = queue[i]->val;
if (queue[i]->left)
queue[rear++] = queue[i]->left;
if (queue[i]->right)
queue[rear++] = queue[i]->right;
}
(*returnSize)++;
}
*returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize));
for (int i = 0; i < *returnSize; i++)
(*returnColumnSizes)[i] = columnSizes[i];
return ans;
}
int main() {
TreeNode *root = createNode(3);
root->left = createNode(9);
root->right = createNode(20);
root->right->left = createNode(15);
root->right->right = createNode(20);
int returnSize;//记录当前层数
int *returnColumnSizes;//存放当前层结点的数组
int **result = levealOrder(root, &returnSize, &returnColumnSizes);
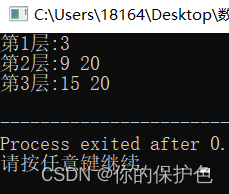
for (int i = 0; i < returnSize; i++) {
cout << "第" << (i + 1) << "层:";
for (int j = 0; j < returnColumnSizes[i]; j++)
cout << result[i][j] << " " ;
cout << endl;
}
for (int i = 0; i < returnSize; i++)
free(result[i]);//动态创建的空间用完之后要释放掉,避免内存泄漏的风险。
free(result);
free(returnColumnSizes);
return 0;
}
结果: