介绍
最近我们被客户要求撰写关于混合效应模型的研究报告,包括一些图形和统计输出。本教程对多层回归模型进行了基本介绍 。
相关视频:线性混合效应模型(LMM,Linear Mixed Models)和R语言实现
线性混合效应模型(LMM,Linear Mixed Models)和R语言实现案例
时长12:13
本教程期望:
- 多层回归模型的基础知识 。
- R中编码的基础知识。
- 安装R软件包
lme4,和lmerTest。
步骤1:设定
如果尚未安装所有下面提到的软件包,则可以通过命令安装它们 install.packages("NAMEOFPACKAGE")。
library(lme4) # 用于分析
library(haven) # 加载SPSS .sav文件
library(tidyverse) # 数据处理所需。
受欢迎程度数据集包含不同班级学生的特征。本教程的主要目的是找到模型和检验关于这些特征与学生受欢迎程度(根据其同学)之间的关系的假设。 我们将使用.sav文件,该文件可以在SPSS文件夹中找到。将数据下载到工作目录后,可以使用read_sav() 命令将其打开 。
GitHub是一个平台,允许研究人员和开发人员共享代码,软件和研究成果,并在项目上进行协作。
步骤2:数据清理
数据集中有一些我们不使用的变量,因此我们可以选择将要使用的变量,并查看前几个观察值。
# 我们只选择将要使用的变量
head(populardata) # 我们来看一下前6个观察样本## # A tibble: 6 x 6
## pupil class extrav sex texp popular
## <dbl> <dbl> <dbl> <dbl+lbl> <dbl> <dbl>
## 1 1 1 5 1 [girl] 24 6.3
## 2 2 1 7 0 [boy] 24 4.9
## 3 3 1 4 1 [girl] 24 5.3
## 4 4 1 3 1 [girl] 24 4.7
## 5 5 1 5 1 [girl] 24 6
## 6 6 1 4 0 [boy] 24 4.7步骤3:绘制数据
在开始分析之前,我们可以绘制外向性和受欢迎程度之间的关系,而无需考虑数据的多层结构。
ggplot(data = populardata,
aes(x = extrav,
y = popular))+
geom_point(size = 1.2,
alpha = .8,
position = "jitter")+# 为绘图目的添加一些随机噪声
theme_minimal()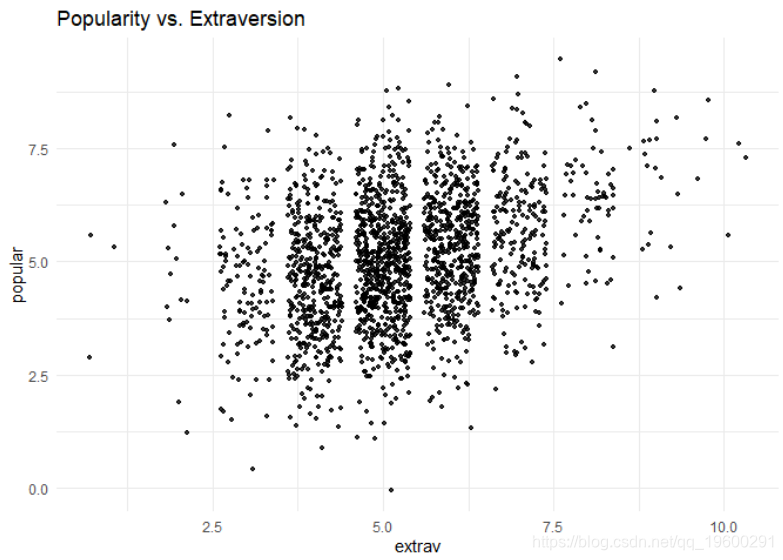
现在我们可以向该图添加回归线。
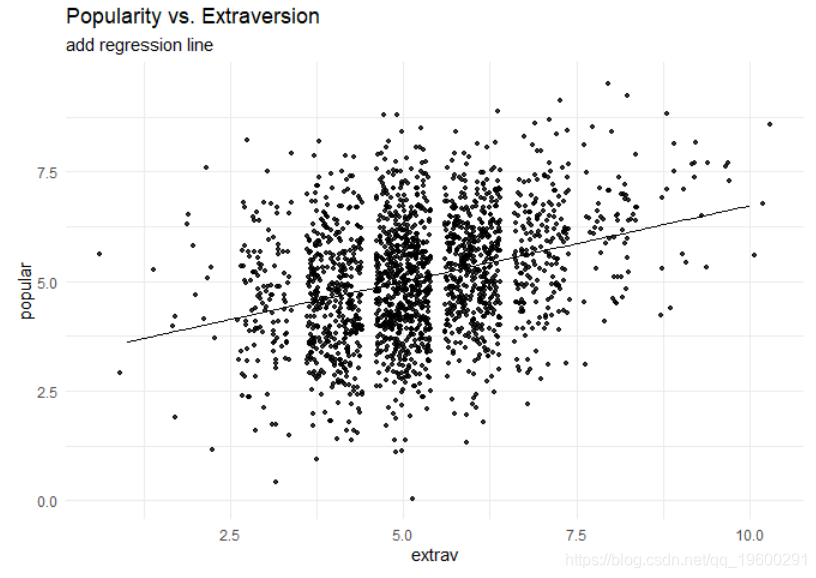
到目前为止,我们已经忽略了数据的嵌套多层结构。我们可以通过对不同类进行颜色编码来显示这种多层结构。
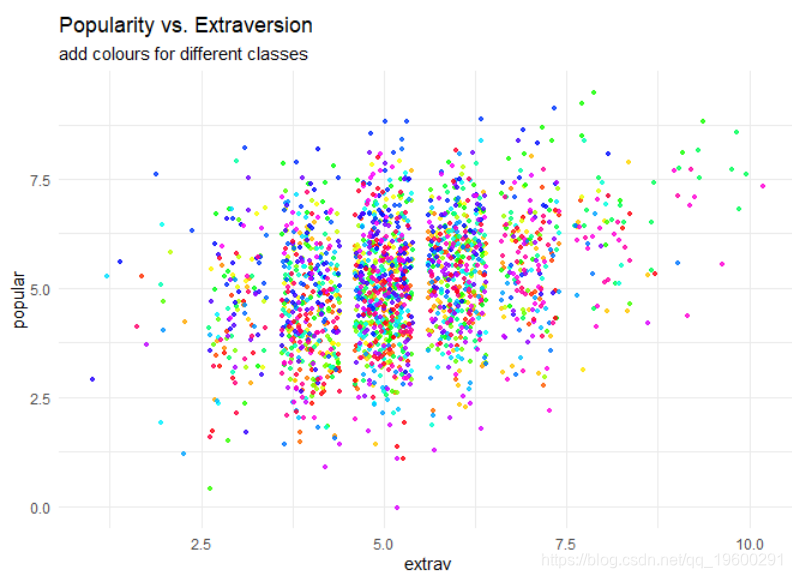
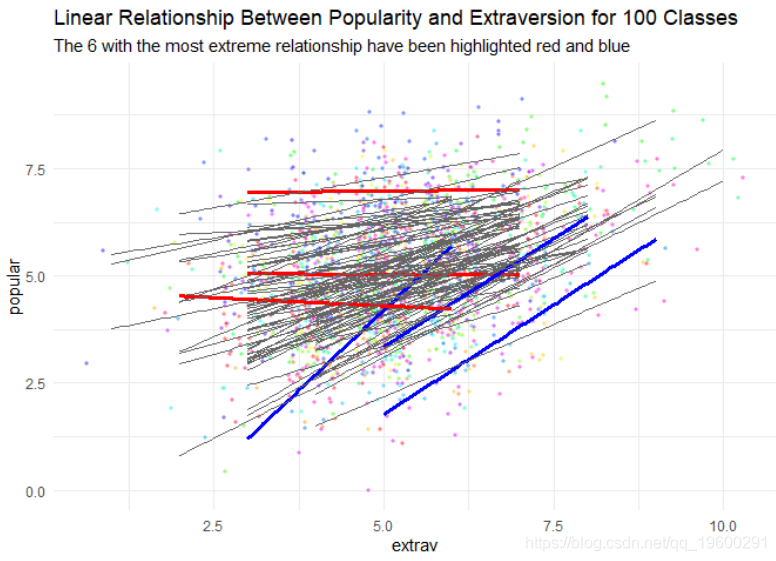
现在我们可以为数据中的100个不同类别绘制不同的回归线
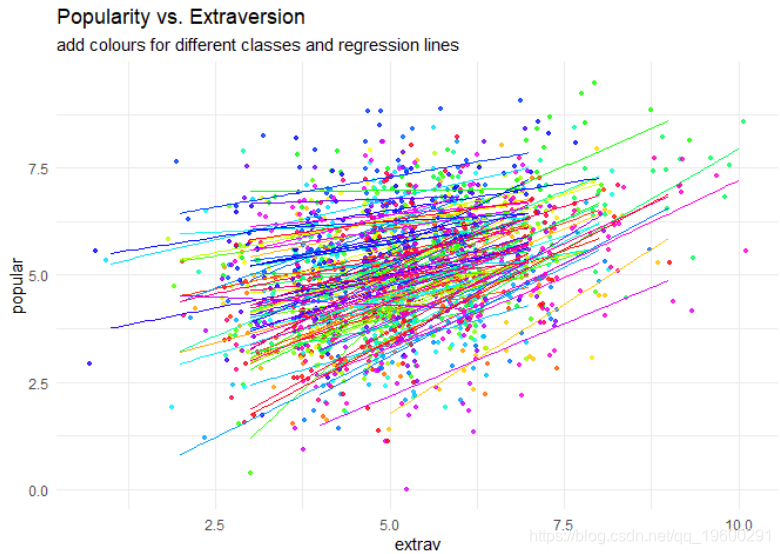
我们清楚地看到,外向性和受欢迎程度之间的关系在所有层级中并不相同,但平均而言,存在明显的正向关系。在本教程中,我们将显示这些不同斜率的估计值(以及如何解释这些差异)。
我们还可以对最极端的回归线进行颜色编码。
人气数据:
f1(data = as.data.frame(popular2data),
x = "extrav",
y = "popular",
grouping = "class",
n.highest = 3,
n.lowest = 3) %>%
ggplot()+
geom_point(aes(x = extrav,
y = popular,
fill = class,
group = class),
size = 1,
alpha = .5,
position = "jitter",
shape = 21,
col = "white")+
geom_smooth(aes(x = extrav,
y = popular,
col = high_and_low,
group = class,
size = as.factor(high_and_low),
alpha = as.factor(high_and_low)),
method = lm,
se = FALSE)+
步骤4:分析数据
截距模型
我们第一个模型是截距模型。
如果我们查看LMER函数的不同输入,则:
- “受欢迎程度”,表示我们要预测的因变量。
- 一个“〜”,用于表示我们现在给出了其他感兴趣的变量。(与回归方程式的'='相比)。
- 公式中表示截距的“ 1”。
- 由于这是仅截距模式,因此我们在这里没有任何其他自变量。
- 在方括号之间,我们具有随机效果/斜率。同样,值1表示垂直“ |”的截距和变量右侧 条用于指示分组变量。在这种情况下,类ID。因此,因变量“受欢迎程度”是由截距和该截距的随机误差项预测的。
- 最后,我们在
data =命令后指定要使用的数据集
summary(interceptonlymodel) #得到参数估计.## 通过REML进行线性混合模型拟合。 t检验使用Satterthwaite的方法
## REML criterion at convergence: 6330.5
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.5655 -0.6975 0.0020 0.6758 3.3175
##
## Random effects:
## Groups Name Variance Std.Dev.
## class (Intercept) 0.7021 0.8379
## Residual 1.2218 1.1053
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 5.07786 0.08739 98.90973 58.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1如果查看汇总输出,则在“随机效应”下可以看到,类别层0.7021上的残差和第一层(学生层)上的残差为1.2218。这意味着类内相关性(ICC)为0.7021 /(1.2218 + 0.7021)=.36。
在“固定效果”下,报告截距的估计值为5.078。
我们还可以输出计算ICC。
## # Intraclass Correlation Coefficient
##
## Adjusted ICC: 0.365
## Conditional ICC: 0.365一层预测变量
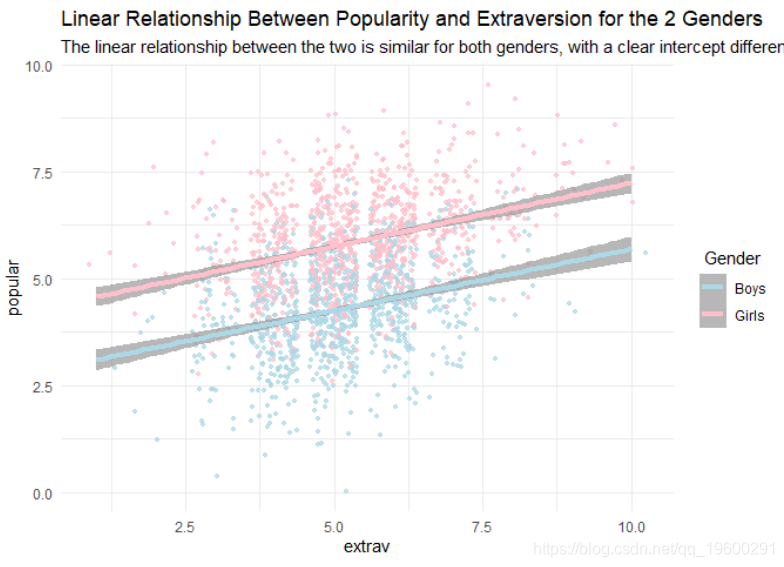
现在我们可以首先添加第一层(学生)水平的预测变量。一层预测因子是性别和外向性。现在,我们仅将它们添加为固定效果,而不添加为随机斜率。在此之前,我们可以绘制两种性别在效果上的差异。我们发现性别之间可能存在平均差异,但斜率(回归系数)没有差异。
summary(model1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Data: popular2data
##
## REML criterion at convergence: 4948.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.2091 -0.6575 -0.0044 0.6732 2.9755
##
## Random effects:
## Groups Name Variance Std.Dev.
## class (Intercept) 0.6272 0.7919
## Residual 0.5921 0.7695
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 2.141e+00 1.173e-01 3.908e+02 18.25 <2e-16 ***
## sex 1.253e+00 3.743e-02 1.927e+03 33.48 <2e-16 ***
## extrav 4.416e-01 1.616e-02 1.957e+03 27.33 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) sex
## sex -0.100
## extrav -0.705 -0.085现在的截距为2.14,性别的回归系数为1.25,外向回归系数为0.44。在输出的固定效果表的最后一列中,我们看到了P值,这些值表示所有回归系数均与0显着不同。
一层和二层预测变量
现在,我们(除了重要的1层变量)还在第2层(教师经验)添加了预测变量。
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Data: popular2data
##
## REML criterion at convergence: 4885
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1745 -0.6491 -0.0075 0.6705 3.0078
##
## Random effects:
## Groups Name Variance Std.Dev.
## class (Intercept) 0.2954 0.5435
## Residual 0.5920 0.7694
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 8.098e-01 1.700e-01 2.264e+02 4.764 3.4e-06 ***
## sex 1.254e+00 3.729e-02 1.948e+03 33.623 < 2e-16 ***
## extrav 4.544e-01 1.616e-02 1.955e+03 28.112 < 2e-16 ***
## texp 8.841e-02 8.764e-03 1.016e+02 10.087 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) sex extrav
## sex -0.040
## extrav -0.589 -0.090
## texp -0.802 -0.036 0.139结果表明,层1和层2变量均显着。但是,我们尚未为任何变量添加随机斜率 。
现在,我们还可以与基础模型相比,计算出第1层和第2层的解释方差。
- 对于1层,这是(1.2218 – 0.592)/1.2218 = 0.52
- 对于2层,这是(0.7021 – 0.2954)/0.7021 = 0.58
具有随机斜率的一层和二层预测模型(1)
现在我们还想包括随机斜率。第1层的两个预测变量(性别和外向性)均具有随机斜率。要在LMER中完成此操作,只需将随机斜率的变量添加到输入的随机部分。 (1|class)变成 (1+sex+extrav |class)。
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Data: popular2data
##
## REML criterion at convergence: 4833.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1643 -0.6555 -0.0247 0.6711 2.9571
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## class (Intercept) 1.341820 1.15837
## sex 0.002395 0.04894 -0.39
## extrav 0.034738 0.18638 -0.88 -0.10
## Residual 0.551448 0.74260
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 7.585e-01 1.973e-01 1.811e+02 3.845 0.000167 ***
## sex 1.251e+00 3.694e-02 9.862e+02 33.860 < 2e-16 ***
## extrav 4.529e-01 2.464e-02 9.620e+01 18.375 < 2e-16 ***
## texp 8.952e-02 8.617e-03 1.014e+02 10.389 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) sex extrav
## sex -0.062
## extrav -0.718 -0.066
## texp -0.684 -0.039 0.089
## convergence code: 0
## Model failed to converge with max|grad| = 0.026373 (tol = 0.002, component 1)我们可以看到所有固定的回归斜率仍然很显着。然而,没有给出对随机效应的显着性检验,但是,可变性别的斜率的误差项(方差)估计很小(0.0024)。这可能意味着类别之间的SEX变量没有斜率变化,因此可以从下一次分析中删除随机斜率估计。由于没有针对此方差的直接显着性检验,我们可以使用 软件包的 ranova() 函数 lmerTest,提供类似于ANOVA的随机效果表。它检查如果删除了某种随机效应(称为似然比检验),则模型是否变得明显更差,如果不是这种情况,则随机效应不显着。
ranova(model3)## ANOVA-like table for random-effects: Single term deletions
##
## Model:
## npar logLik AIC LRT Df
## <none> 11 -2416.6 4855.3
## sex in (1 + sex + extrav | class) 8 -2417.4 4850.8 1.513 3
## extrav in (1 + sex + extrav | class) 8 -2441.9 4899.8 50.506 3
## Pr(>Chisq)
## <none>
## sex in (1 + sex + extrav | class) 0.6792
## extrav in (1 + sex + extrav | class) 6.232e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1我们看到性别的随机影响确实不显着(P = 0.6792),外向的随机影响也很显着(P <.0001)。
具有随机斜率的一层和二层预测模型
我们在忽略性别的随机斜率之后继续。
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Data: popular2data
##
## REML criterion at convergence: 4834.8
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1768 -0.6475 -0.0235 0.6648 2.9684
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## class (Intercept) 1.30296 1.1415
## extrav 0.03455 0.1859 -0.89
## Residual 0.55209 0.7430
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 7.362e-01 1.966e-01 1.821e+02 3.745 0.000242 ***
## sex 1.252e+00 3.657e-02 1.913e+03 34.240 < 2e-16 ***
## extrav 4.526e-01 2.461e-02 9.754e+01 18.389 < 2e-16 ***
## texp 9.098e-02 8.685e-03 1.017e+02 10.475 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) sex extrav
## sex -0.031
## extrav -0.717 -0.057
## texp -0.688 -0.039 0.086我们看到:
- 截距是0.736
- 性别的固定影响是1.252
- 老师经验的影响是0.091
- 外向的平均影响为0.453
- 外向斜率的随机效应为0.035
- 一层残差为0.552
- 二层的残差为1.303
具有随机斜率和跨水平交互作用的一层和二层预测
作为最后一步,我们可以在教师的经验和外向性之间添加跨层的交互作用。换句话说,我们要调查的是,班上外向与受欢迎程度之间关系的差异是否可以由该班老师的老师经验来解释。 我们添加了Extraversion和Teacher体验之间的层级交互项。这意味着我们必须添加TEXP作为EXTRAV系数的预测因子。外向性和教师经验之间的跨层级交互作用可以通过“:”符号或乘以符号来创建。
如果将所有这些都以公式形式表示,则得到:
受欢迎程度ij =β0j+β1* genderij +β2j* extraversionij + eij
受欢迎程度ij =β0j+β1* genderij +β2j* extraversionij + eij。
其中β0j=γ00+γ01∗ experiencej +u0jβ0j=γ00+γ01∗ experiencej + u0j和β2j=γ20+γ21∗ experiencej +u2jβ2j=γ20+γ21∗ experiencej + u2j
合并得到:
受欢迎程度ij =γ00+γ10∗ sexij +γ20∗ extraversionij +γ01∗经验j +γ21∗ extraversionij ∗经验j + u2j ∗ extraversionij + u0j + eij
受欢迎程度ij =γ00+γ10∗ sexij +γ20∗ extraversionij +γ01∗经验j +γ21∗ extraij u2j * extraversionij + u0j + eij
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Data: popular2data
##
## REML criterion at convergence: 4780.5
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.12872 -0.63857 -0.01129 0.67916 3.05006
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## class (Intercept) 0.478639 0.69184
## extrav 0.005409 0.07355 -0.64
## Residual 0.552769 0.74348
## Number of obs: 2000, groups: class, 100
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) -1.210e+00 2.719e-01 1.093e+02 -4.449 2.09e-05 ***
## sex 1.241e+00 3.623e-02 1.941e+03 34.243 < 2e-16 ***
## extrav 8.036e-01 4.012e-02 7.207e+01 20.031 < 2e-16 ***
## texp 2.262e-01 1.681e-02 9.851e+01 13.458 < 2e-16 ***
## extrav:texp -2.473e-02 2.555e-03 7.199e+01 -9.679 1.15e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) sex extrav texp
## sex 0.002
## extrav -0.867 -0.065
## texp -0.916 -0.047 0.801
## extrav:texp 0.773 0.033 -0.901 -0.859交互项用extrav:texp 表示, Fixed effects 并估计为-0.025。
从这些结果中,我们现在还可以通过使用教师经验作为第二层变量来计算解释的外向斜率方差:(0.03455-0.005409)/0.03455 = .843。因此,外向斜率回归系数的方差的84.3%可以由老师的经验来解释。
外向系数在受欢迎程度上的截距和斜率均受教师经验的影响。一名具有0年经验的老师的班级中,外向得分为0的男学生(SEX = 0)的预期受欢迎度为-1.2096。一名类似的(男)学生,每增加1分外向度,就将获得0.8036分,以提高其知名度。当教师经验增加时,每年经验的截距也增加0.226。因此,同一个没有外向性的男学生与一个有15年经验的老师一起上课,其预期受欢迎度得分为-1.2096 +(15 x .226)= 2.1804。教师的经验也减轻了外向性对普及的影响。对于具有15年经验的教师,外向的回归系数仅为0.8036 –(15 x .0247)= 0.4331(相比之下,具有0年经验的教师班级为0.8036)。
我们还可以清楚地看到,多年的教师经验既影响截距,又影响外向度的回归系数。
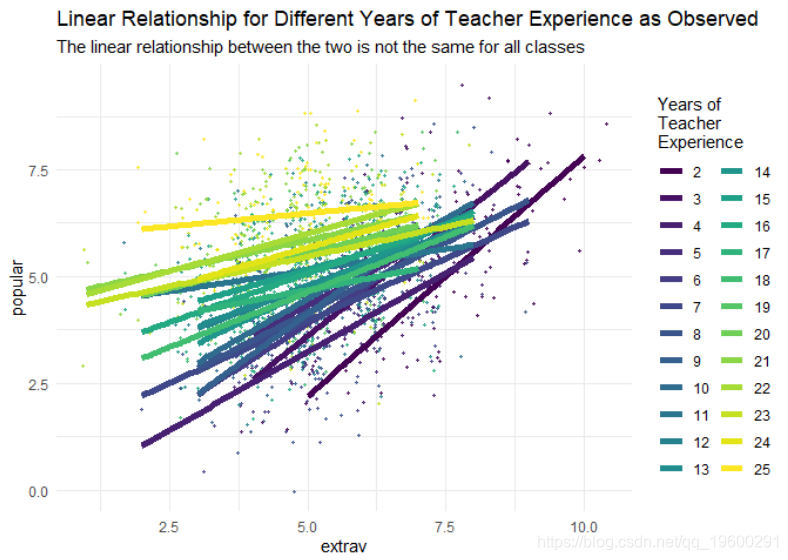
最后
在本教程结束,我们将检查模型的残差是否正态分布(在两个层级上)。除了残差是正态分布的之外,多层模型还假设,对于不同的随机效应,残差的方差在组(类)之间是相等的。确实存在跨组的正态性和方差相等性的统计检验。
首先,我们可以通过比较残差和拟合项来检查均方差。
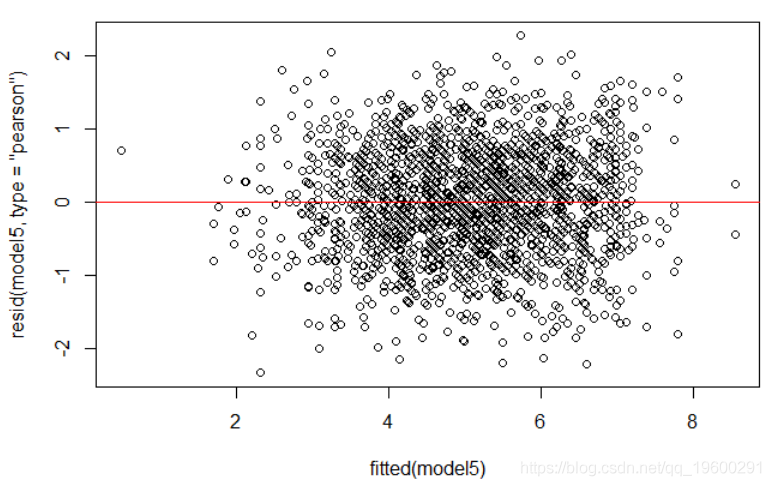
我们还可以使用QQ图检查残差的正态性。该图确实表明残差是正态分布的。
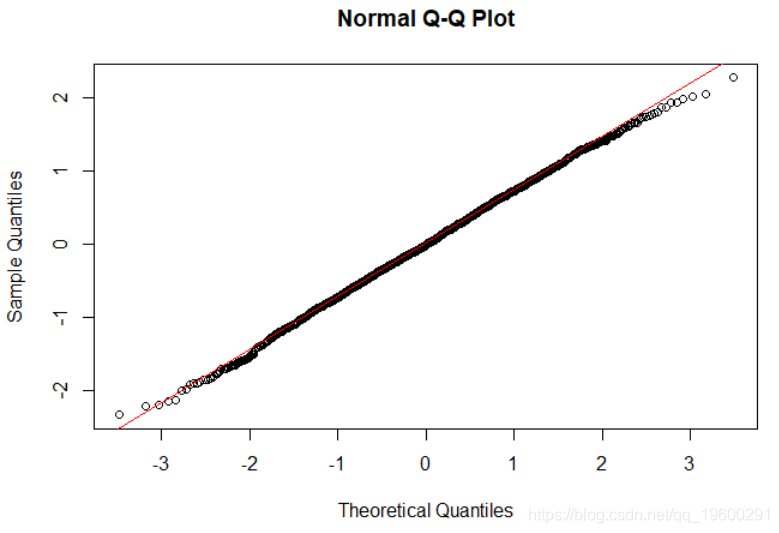
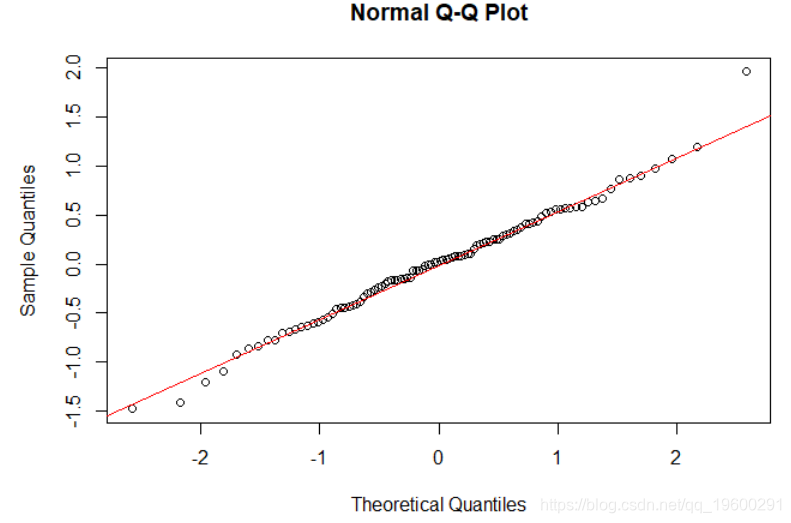
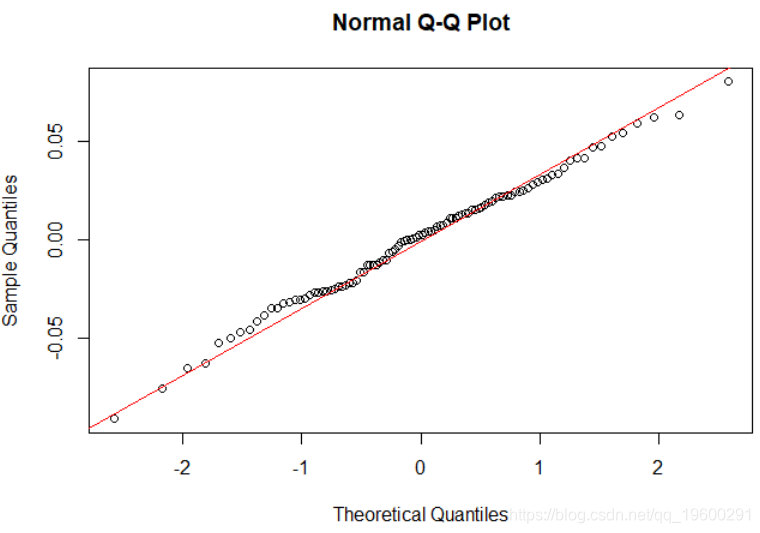
现在,我们还可以检查100个班级的两个随机效果。同样,可以看到符合正态分布。






![[UE5]在多个固定摄像机视角间切换,切换多个摄像机,显示不同摄像机所看内容](https://img-blog.csdnimg.cn/ccc18f7c0faa483d9add9d897f4d0752.png)