0-1背包理论基础详解

news2025/1/16 2:53:09

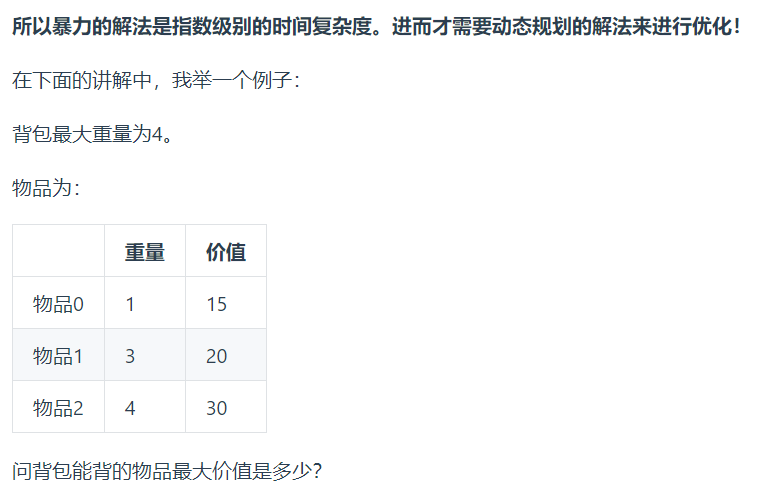
0-1背包问题：有 n 种物品，每种物品只有1个，求解将哪些物品装入背包里物品价值总和最大。

图片来自：代码随想录

0-1背包问题举例：

题目描述：

使用二维dp数组解决背包问题

动规五部曲：

dp[i][j]： [0,i] 0~i 之间物品任取放入容量为 j 的背包

不放物品 i：dp[i-1][j] 不放物品 i,就是从0~（i-1）
放物品 i：dp[i-1][j - weight[i]] + value[i] 如果放物品 i，则需要从背包中减掉物品 i 的重量，然后再加上物品 i 的价值
- 解释：dp[i-1][j - weight[i]] ：表示背包中不放物品 i ，并且背包的容量减去物品 i 的重量后，此时背包所能放的最大价值。
- 此时再加上物品 i 的重量，则此时背包的最大价值为在刚才的基础之上再加上 value[i]。

根据不放物品和放物品的情况，则递推公式为：dp[i][j]=Math.max(dp[i-1][j] , dp[i-1][j - weight[i]] + value[i])
初始化：初始化第一行和第一列，dp[0][0]=
遍历顺序：一般是有2层for循环，一层遍历背包，一层遍历物品，有时候for循环
对于dp数组是二维数组时，即2层for循环的0-1背包问题，则2层for循环遍历顺序是可以颠倒的！
但是对于一维dp数组，即滚动数组，情况需另行分析。

1.1、使用一维dp数组解决背包问题

代码实现：

package bag_problem;

import java.util.Arrays;

/**
 * @author: Arbicoral
 * @Description: 二维dp数组实现 0-1背包问题
 */
public class Bag01 {
    public static void main(String[] args) {
        int n = 3;// 共有 3个物品
        int bagSize = 4;// 背包的最大重量是 4
        int[] weight = new int[]{1, 3, 4};// 物品重量
        int[] value = new int[]{15, 20, 30};// 物品价值
        bagProblemSolution(n, bagSize, weight, value);
    }

    private static void bagProblemSolution(int n, int bagSize, int[] weight, int[] value) {
        // 1. 定义dp[][]
        int[][] dp = new int[n][bagSize + 1];
        // 2. 初始化dp[][]
        // 初始化第一列为 0 ，默认都是 0
        // 初始化第一行
        for (int i = 1; i <= bagSize; i++) {
            if (i >= weight[0]) {
                dp[0][i] = value[0];
            }
        }
        // 打印初始化后的dp数组
        System.out.println("打印初始化后的dp数组:");
        for (int[] i : dp) {
            System.out.println(Arrays.toString(i));
        }
        // 3. 遍历：填充dp[][]
        for (int i = 1; i < n; i++) {// 放置物品的个数
            for (int j = 1; j <= bagSize; j++) {// 遍历 背包
                if (j < weight[i]) {
                    // 如果背包的容量 < 物品i的重量，则dp[i][j]和上面的保持一致
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 如果背包的容量 >= 物品i的重量，按照递推公式即可
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                    // System.out.println("dp[" + i + "][" + j + "] = " + dp[i][j]);
                }
            }
        }
        System.out.println("--------------");
        // 打印dp数组
        System.out.println("填充后的dp数组:");
        for (int[] i : dp) {
            System.out.println(Arrays.toString(i));
        }
    }
}

输出结果：

1.2、使用一维dp数组解决背包问题

本质：将二维dp数组降为一维dp数组，每次将二维dp数组的行复制后再更新复制后的行。（可能有点绕）

动规五部曲：

dp[j] ：背包为 j 的容量最多能装的物品价值；
递推公式：dp[j]=Math.max(dp[j]，dp[j - weight[i]] + value[i]) 不放物品 i ：dp[j] 放物品 i ：dp[j - weight[i]] + value[i]
初始化：dp[0]=0; dp[1]=
遍历顺序：倒序遍历，因为一维dp数组中是重复利用的，旧值和当前需要的值会有冲突；
先遍历物品，再遍历背包。

代码实现：

package bag_problem;

import java.util.Arrays;

/**
 * @author: Arbicoral
 * @Description: 一维dp数组实现 0-1背包问题
 */
public class Bag01OneDimension {
    public static void main(String[] args) {
        int n = 3;// 共有 3个物品
        int bagSize = 4;// 背包的最大重量是 4
        int[] weight = new int[]{1, 3, 4};// 物品重量
        int[] value = new int[]{15, 20, 30};// 物品价值
        bagProblemOneDimensionSolution(n, bagSize, weight, value);
    }

    private static void bagProblemOneDimensionSolution(int n, int bagSize, int[] weight, int[] value) {
        // 1. 定义dp[]
        int[] dp = new int[bagSize + 1];
        // 2. 初始化dp[]
        // 初始化第一列为 0 ，默认都是 0
        // 打印初始化后的dp数组
        System.out.println("打印初始化后的dp数组:");
        System.out.println(Arrays.toString(dp));

        System.out.println("填充后的dp数组:");
        // 3. 遍历：填充dp[]
        for (int i = 0; i<n; i++) {
            for (int j = bagSize; j >= weight[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
            // 打印dp数组
            System.out.println(Arrays.toString(dp));
        }
    }
}