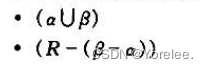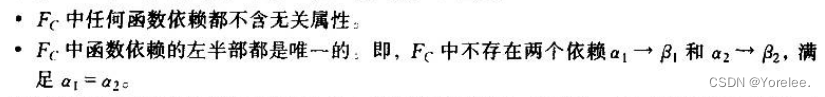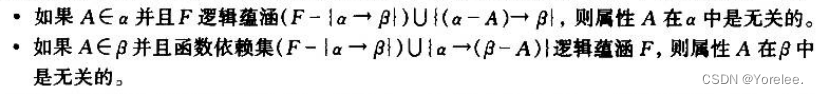一、范式
一、BC范式(BCNF)
(1)定义
BC范式可以消除所有利用函数依赖发现的冗余
范式是对于关系模式而言的,即可以说关系模式R是一个范式。
因此对于BC范式,它需要满足的条件是,对于它的所有函数依赖α→β至少有以下之一:
(2)分解不属于BC范式的模式
如果R中存在一个非平凡的函数依赖α→β,且α不是超码。则我们需要用以下两个模式取代R
①由于α可以决定β,我们提取出一个以α为超码的关系,它包含α和β的属性。
②原来的R保留α中的不同于β的部分,其余β部分去掉,我们想保留另一个关系的主码。以便于自然连接无损。
这种分解是无损连接分解,因为②中保留了①中的超码,因此自然连接时可以有足够的信息。但是①和②都不一定是BC范式,可能需要进一步分解,但最终不能分解时则全都是BC范式。(比如①中若仍然有非平凡依赖β→γ,而超码是α,不是β)。
缺点:可能在分解的过程中可能不能保持依赖,即分解后两个关系的依赖 重新合并在原关系下 也推导不出原来的全部函数依赖。
(3)How good is BCNF?
如下关系模式:
(employee_id,dname,phone_number),若一个id为999-99-9999的雇员,有两个亲属分别为“David”和“William”,有两个电话号码。可以发现这是一个只有平凡依赖的关系模式,因此是BCNF范式,但是这样的合并相当的冗余。比如我们要为其加入一个新电话,那么需要加两个元组,分别包含两个亲属的名字。
因此我们需要更高的函数依赖。
(4)保持依赖
只能降低规范化标准:第三范式
二、第三范式(3NF)
(1)定义
对于第三范式,它需要满足的条件是,对于它的所有函数依赖α→β至少有以下之一:
可以看出BC范式一定满足前两个,所以BC范式一定是第三范式,但是第三范式不一定是BC范式,第三范式属于是BC范式为了保持原来的函数依赖降低了要求。
第三个条件是BC范式保持函数依赖的最小松弛(放宽)
二、函数依赖理论
一、函数依赖集的闭包
(1)定义
对于给定关系模式R,R上的依赖集F,F所逻辑蕴含的(F所能推导出的)所有函数依赖的集合
,称为F的闭包。
(2)计算(用函数依赖 推导 其蕴含的函数依赖)
①阿姆斯特朗公理
注意:αβ指的是α∪β(属性集的并集),所以αα=α
阿姆斯特朗公理可以推导出F的闭包,但是相当麻烦。(不会要求计算F的闭包)
②更简化规则
要求证明
1°合并律:
增补律:由α→β,可得α→βα
由α→γ,可得βα→βγ
传递律:由α→βα和βα→βγ,可得α→βγ
2°分解律:
自反律:由β、γ均包含于βγ,可得βγ→β,βγ→γ
传递律:由α→βγ,及βγ→β,βγ→γ,可得α→β、α→γ
3°伪传递律:
增补律:由α→β,可得αγ→βγ(βγ=γβ 并集!)
传递律:由αγ→βγ,γβ→δ,可得αγ→δ。
注:
左边→右边,左右两边同时包含的,右边的可以去掉,因为自己一定知道自己。另外,右边直接加上左边的也是可以的(满足增补律,也满足自己知道自己)。
并且左边→右边,在左边加上任何属性,仍然有左右∪{**}→右边,因为对于一个元组而言已知这个左边的信息就已经确定了它这个右边的信息,再加上一些信息,它还是可以确定这个右边的信息。(实际上是自反律和传递律,左右∪{**}→左边→右边)
比如A→B, 则可以有 A→AB,AG→B。
③枚举所有属性集,求其闭包,列出所有函数依赖求解
二、属性集的闭包
(1)定义
在函数依赖集F下由α函数确定的所有属性的集合为F下α的闭包,记作
。
F是能确定关系R所有函数依赖的函数依赖集,这样才有意义。所以α的闭包是α在R中,一旦一个元组的α确定,它所能确定的R中的属性。
(2)计算方法
具体来说就是,首先α属性进入result集合,扫描函数依赖集F,对于每一条函数依赖,若其左部的属性包含在result中,则将右部的新属性加入result,依此下去,循环扫描直至没有更新。
(3)属性集闭包的用途
对于关系R中的属性集α的闭包
1°可以判定α是否是超码,只要它的闭包包含了所有属性,则α是超码。(候选码需要再判断)
2°检验是否有α→β成立,只要β包含于
即可。
3°用于计算函数依赖集F的闭包:
对于R的任意非空属性集,计算其闭包,然后即可得到以该属性集为左部的所有函数依赖。
由于左部包含了任意R的非空属性集,则所有R的函数依赖都包含了,即F的闭包求出来了。
三、正则覆盖
(1)定义
F的正则覆盖Fc是一个依赖集,并且他们互相蕴含。满足:
即Fc是关系R上的最简化函数依赖集,不包含冗余部分,F和Fc具有相同的闭包。
正则覆盖不一定唯一。
(2)无关属性
对于F中的函数依赖α→β:
去掉要检验的属性A后,得到的新依赖集F',
若A在左部,判断F是否蕴含F' (即F能否推出α-{A}→β)
若A在右部,判断F'是否蕴含F (即F’能否推出α→A)
计算方法:
(3)正则覆盖的计算方法
删除后若为空,则删除该函数依赖,换句话说如果一个函数依赖的右部只有一个属性,它也可能是无关属性。
在检验时用的是当前Fc上的函数依赖,本质就是Fc当做F,Fc删除后的当做F',没什么区别。
四、无损连接分解
如果R1和R2是R的无损连接分解,如果以下函数依赖中至少有一个属性F的闭包:
即分解时,分解后的共同部分是某一个关系的超码,那么在自然连接时就可以通过这个超码唯一确定元组。(BC范式就满足这样的分解)
注:这是一个充分非必要条件,无损连接分解不一定满足该条件,只有当所有约束都是函数依赖的时候才是一个充要条件。
没有保持依赖的性质。
五、保持依赖
(1)定义
即分解后的属性集合R1,R2……,Rn,在F闭包上只包含Ri的所有函数依赖集F1,F2……,Fn,它们的并集在R上能够蕴含F。
例如:
inst_dept(ID,name,salary,dept_name,building,budget)的函数依赖F集有{ID->R,dept_name->building,budget};
分解为
instructor(ID,name,salary,dept_name) F1={ID->ID,name,salary,dept_name}
department(dept_name,building,budget) F2={dept_name->building,budget}
F1∪F2 的闭包显然蕴含F,即F1∪F2的闭包与F的闭包相同
则该分解是保持依赖的,同时这分解后也是两个BC范式。
(2)计算方法
对于F上的每一个α→β使用:
本质上求的是α在F'上的闭包,判断其闭包是否包含β,包含的话则α→β是被保持的。
但是计算时并未求F',而是利用其等价方式求解:
result表示到目前为止α能够推导出的属性集合,
对于每一个Ri,求result∩Ri在F上的闭包 ,其闭包再与Ri相交得到t,t并入result继续求解,这个求解过程和求result∩Ri在Fi上的闭包是一样的。
考虑如下(乱):求result∩Ri在F上的闭包 无异于 求result∩Ri在F闭包 上的闭包,求解时把F闭包分为两部分,一部分函数依赖左部只包含result∩Ri的属性(这一部分求解的闭包∩Ri和 result∩Ri在Fi上的闭包是是一样的),另一部分左部不止包含这些属性(这一部分求解出的另外的闭包若不是Ri中的属性其实可以由后续循环得到)