前置知识

今天的三道题都聚焦完全背包问题, 关于完全背包, 基础性的思路可以参考上一篇文章
本文的很多操作就是在完全背包的基础上进行修改.

参考文章：
LeetCode刷题笔记【29】：动态规划专题-1（斐波那契数、爬楼梯、使用最小花费爬楼梯）
LeetCode刷题笔记【30】：动态规划专题-2（不同路径、不同路径 II）
LeetCode刷题笔记【31】：动态规划专题-3（整数拆分、不同的二叉搜索树）
LeetCode刷题笔记【32】：动态规划专题-4（二维背包问题、一维背包问题、分割等和子集）
LeetCode刷题笔记【33】：动态规划专题-5（最后一块石头的重量 II、目标和、一和零）
LeetCode刷题笔记【34】：动态规划专题-6（完全背包、零钱兑换II、组合总合IV）

70. 爬楼梯 （进阶）

题目描述

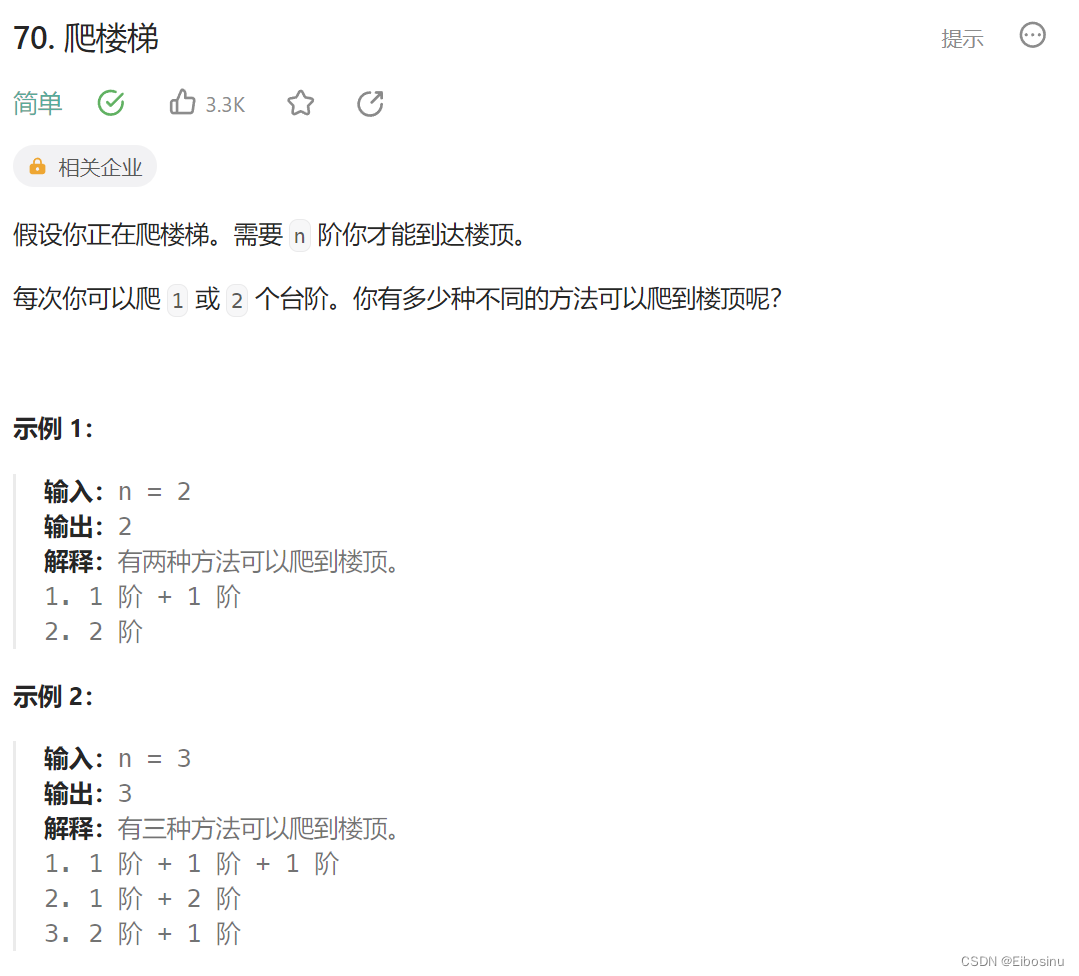
LeetCode链接：https://leetcode.cn/problems/climbing-stairs/description/

解题思路

这道题我们之前有做过, 用的是简单动态规划的思想, 可以参考前文(点击文字跳转).

但是现在用完全背包的视角来看, 可以视为背包大小为n, 有大小为1和2的两种数量不限的物品, 要让我们求有多少种方法可以装满背包.

需要注意的点为:

1. 递推公式为dp[j] = dp[j] + dp[j-i];
2. dp[0] = 1;
3. 因为要求的是排列, 所以外层遍历背包容量j, 内层遍历物品i

代码

动态规划代码:

class Solution {
public:
    int climbStairs(int n) {
        if(n==0 || n==1)
            return 1;
        int first=1, second=1;
        for(int i=2; i<=n; ++i){
            int tmp = first + second;
            first = second;
            second = tmp;
        }
        return second;
    }
};

完全背包代码:

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n+1, 0);
        dp[0] = 1;
        for(int j=1; j<=n; ++j){
            for(int i=1; i<=2; ++i){
                if(j-i>=0)
                    dp[j] = dp[j] + dp[j-i];
            }
        }
        return dp.back();
    }
};

可以看出: 完全背包解法的代码和注意事项都和<377. 组合总和 Ⅳ>很像.

322. 零钱兑换

题目描述

LeetCode链接：https://leetcode.cn/problems/coin-change/description/

解题思路

如果之前不了解动态规划和完全背包的话, 这道题难度是比较高的.
但是经历过之前这一波的毒打, 我们可以一眼看出这一定要用完全背包做(给无限量的xx, 需要凑齐xx量).

前面遇到过<518. 零钱兑换II>, 我们要注意对比这两道题, 会发现无论是初始化方式, 递推公式, 判断条件, 还有是否需要注意内外层顺序, 二者都有差别.

关键就是, <518. 零钱兑换II>要求的是"有多少种方法凑够", 而本题要求的是"凑够给定的数额最少需要多少"

需要注意的有这几点:

1. 初始化时dp数组其他元素为INT_MAX, dp[0]=0;
2. 递推公式为: dp[j] = min(dp[j], 1+dp[j-coins[i]]);
3. 因为有无法填满背包的情况, 所以在过程中要加判断if(dp[j-coins[i]]!=INT_MAX)
4. 要求的是"最少需要的硬币个数", 而不是"需要最少的硬币个数的组合/排列", 所以不用考虑内外层先遍历物品i还是背包容量j的问题, 怎么遍历结果都一样.

以题目中示例1为例, dp数组更新过程如下:

可以看到, 当时推导的时候还在右上角纠结了一下内外层, 其实没有必要, 都一样.

PS: 尤其需要注意的是第3点, 因为可能会有凑不齐的情况, 比如题目给的示例2和示例3, 以实例2为例:

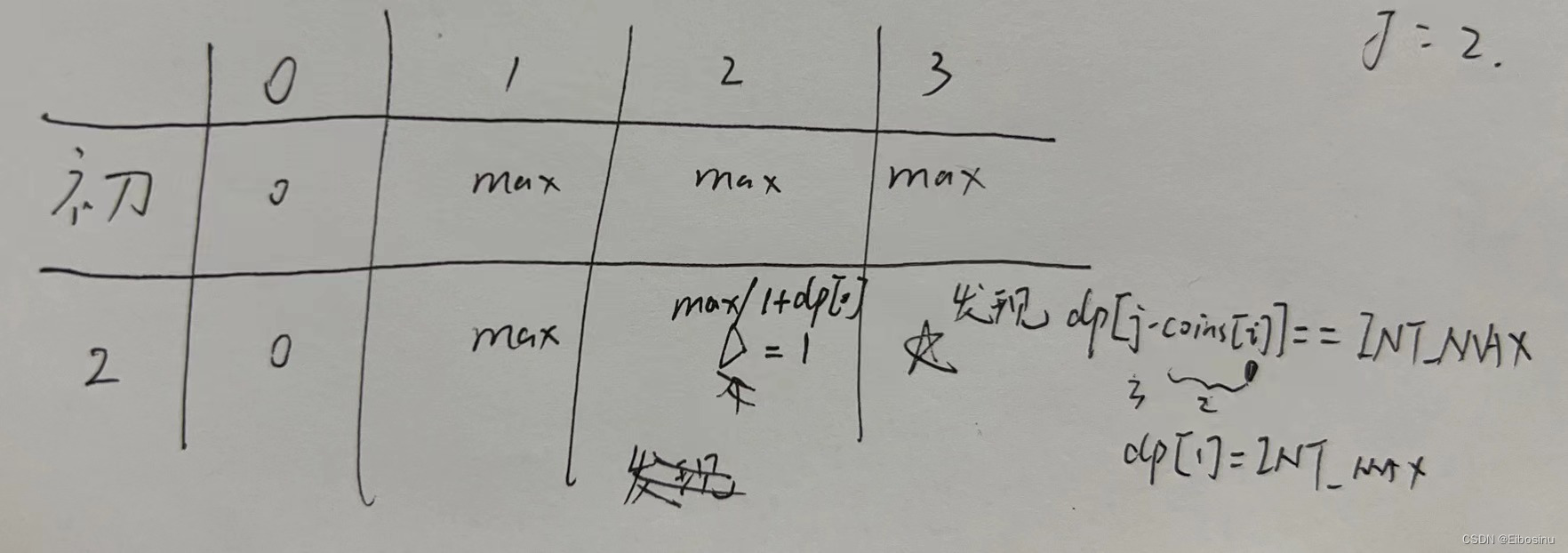
只有加了if(dp[j-coins[i]]!=INT_MAX)的判断, 才可以将这种凑不齐的情况找出来, 并return -1

代码

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1, INT_MAX);
        dp[0] = 0;
        for(int i=0; i<coins.size(); ++i){
            for(int j=1; j<=amount; ++j){
                if(j-coins[i]>=0 && dp[j-coins[i]]!=INT_MAX){
                    dp[j] = min(dp[j], 1+dp[j-coins[i]]);
                }
            }
        }
        if(dp[amount]==INT_MAX)
            return -1;
        return dp[amount];
    }
};

// 优化了一下
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1, INT_MAX);
        dp[0] = 0;
        for(int i=0; i<coins.size(); ++i){
            for(int j=coins[i]; j<=amount; ++j){
                if(dp[j-coins[i]]!=INT_MAX){
                    dp[j] = min(dp[j], 1+dp[j-coins[i]]);
                }
            }
        }
        if(dp[amount]==INT_MAX)
            return -1;
        return dp[amount];
    }
};

279.完全平方数

题目描述

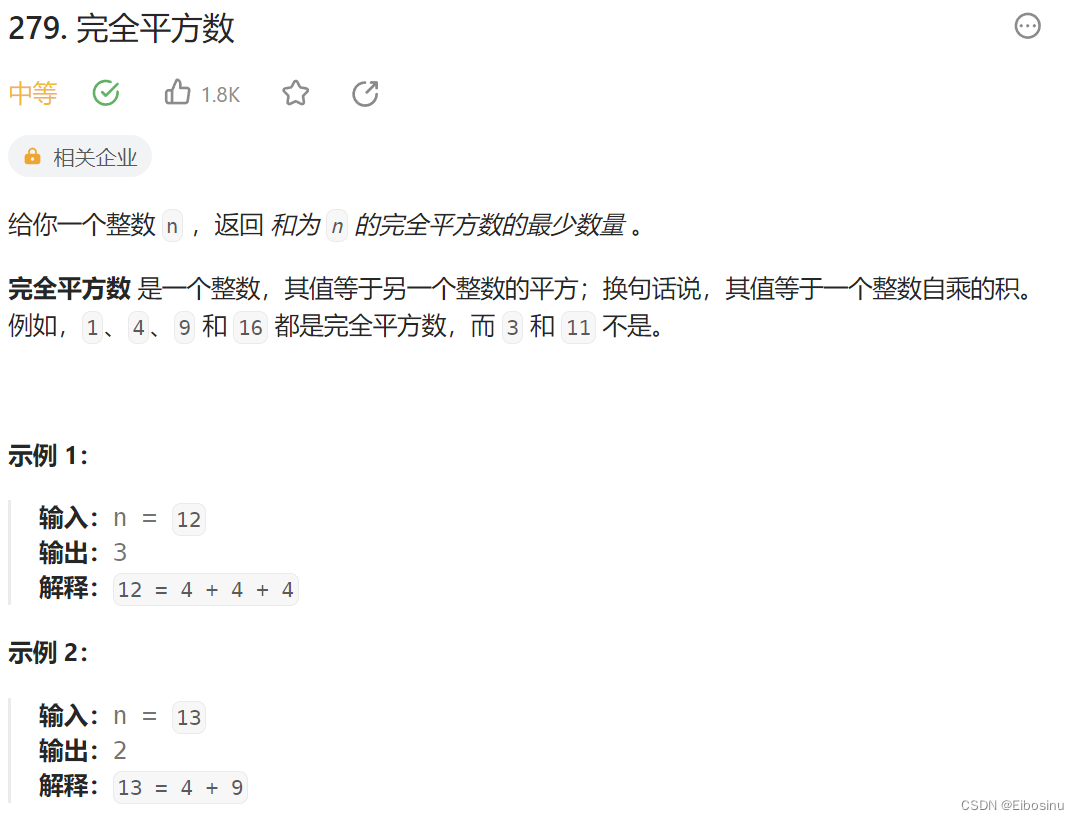
LeetCode链接：https://leetcode.cn/problems/perfect-squares/description/

解题思路

思路和上一题基本一样, 只不过是刚才的物品是coins, 现在物品是i*i, 并且因为有1*1=1, 所以不用考虑凑不齐的问题.

代码

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1, INT_MAX);
        dp[0] = 0;
        vector<int> nums;
        for(int i=1; ; ++i){
            if(i*i <= n)
                nums.push_back(i*i);
            else
                break;
        }
        for(int i=0; i<nums.size(); ++i){
            for(int j=nums[i]; j<=n; ++j){
                dp[j] = min(dp[j], 1+dp[j-nums[i]]);
            }
        }
        return dp.back();
    }
};

// 让写法简洁一些
class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1, INT_MAX);
        dp[0] = 0;
        for(int i=1; i*i<=n; ++i){
            for(int j=i*i; j<=n; ++j){
                dp[j] = min(dp[j], 1+dp[j-i*i]);
            }
        }
        return dp.back();
    }
};

总结

今天是昨天的完全背包问题的进一步深化和拓展, 需要着重进行比较和辨析.
尤其是今天的零钱兑换, 和昨天的零钱兑换IV.

经过这段时间的背包问题折磨, 基本可以比较顺畅的想到背包问题了, 但是在实践过程中, 如何快速抽象出物品, 背包容量等要素, 同时避免"手里是锤子, 看啥都是钉子"的思维定式, 还是要在不断地训练中提升.

本文参考：
爬楼梯
零钱兑换
完全平方数