优质博文:IT-BLOG-CN
一、题目
给定一个二叉树root,返回其最大深度。
二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
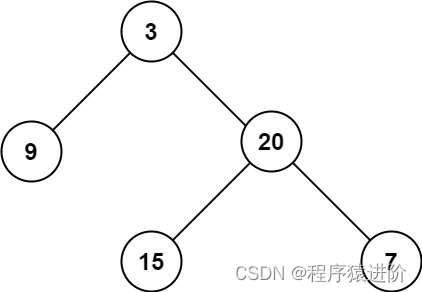
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100
二、代码
【1】深度优先搜索: 如果我们知道了左子树和右子树的最大深度l和r ,那么该二叉树的最大深度即为max(l,r)+1 。而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
// 递归计算数的深度,确定递归的推出条件
if (root == null) {
return 0;
} else {
int leftHight = maxDepth(root.left);
int rightHight = maxDepth(root.right);
return Math.max(leftHight,rightHight) + 1;
}
}
}
复杂度分析:
1、时间复杂度: O(n)其中n为二叉树节点的个数。每个节点在递归中只被遍历一次。
2、空间复杂度: O(height)其中height表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
【2】广度优先搜索: 我们也可以用「广度优先搜索」的方法来解决这道题目,但我们需要对其进行一些修改,此时我们广度优先搜索的队列里存放的是当前层的所有节点。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量ans来维护拓展的次数,该二叉树的最大深度即为ans。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
// 先存放root节点
queue.offer(root);
// 总长度
int maxLen = 0;
// 开启循环,并确定退出循环的条件
while (!queue.isEmpty()) {
// 获取当前队列的长度,确定该层遍历的次数
int size = queue.size();
// 我们需要遍历当前层的所有 treeNode
// 确定循环条件,并确定退出条件
while (size > 0) {
TreeNode treeNode = queue.poll();
if (treeNode.left != null) {
// 注意:添加的时左节点,而不是当前节点
queue.offer(treeNode.left);
}
if (treeNode.right != null) {
queue.offer(treeNode.right);
}
--size;
}
++maxLen;
}
return maxLen;
}
}
复杂度分析:
1、时间复杂度: O(n)其中n为二叉树的节点个数。与方法一同样的分析,每个节点只会被访问一次。
2、空间复杂度: 此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到O(n)。