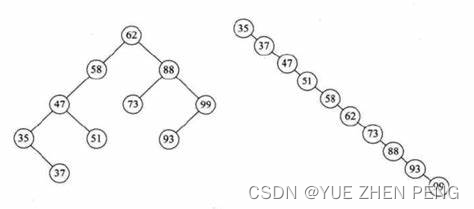
二叉查找树
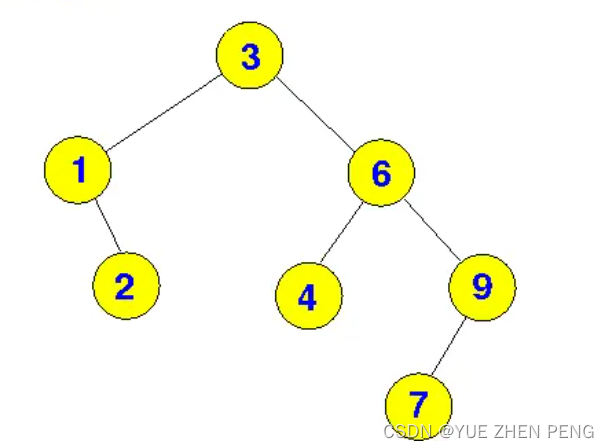
需要满足这些规则:
- 左子节点小于父节点
- 右子节点大于父节点
查找的效率
非常好,每次都能根据大小去舍弃另一半的分支,极大的减少的比对次数
具体的性能,取决于树的层数和平衡程度。
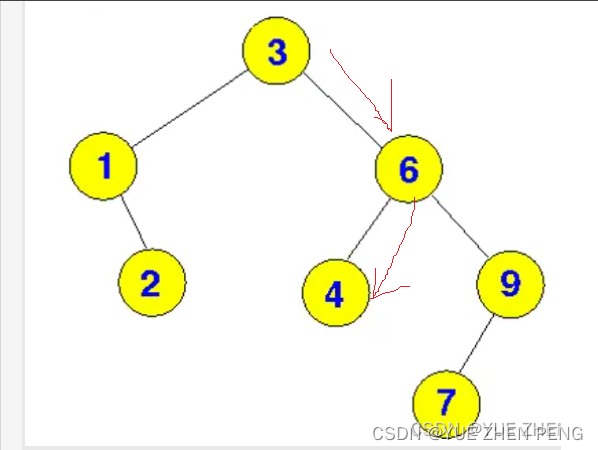
BST树的节点
struct Node
{
Node* parent;
Node* left;
Node* right;
int val;
}
BST的插入
bool Insert(Node* root,Node* newNode)
{
Node* head =nullptr;
if(root==nullptr)
{
*root = *newNode;
return true;
}
Node* current = root;
while(current!=nullptr)
{
if(newNode->val==current->val) return nullptr;
else if(newNode->val>current->val)
{
if(current->right==nullptr)
{
current->right = newNode;
newNode->parent = current;
}
current = current->right;
}
else if(newNode->val<current->val)
{
if(current->left==nullptr)
{
current->left = newNode;
newNode->parent = current;
}
current = current->left;
}
}
return head;
}
BST查找
Node* Search(Node* root, int target)
{
Node* current = root;
while (current != nullptr)
{
if (target == current->val)
{
return current; // 找到目标节点,返回它
}
else if (target < current->val)
{
current = current->left; // 目标值较小,向左子树查找
}
else
{
current = current->right; // 目标值较大,向右子树查找
}
}
return nullptr; // 未找到目标节点
}
BST删除
BST的删除比较复杂,需要先了解二叉树的遍历顺序
《二叉树》
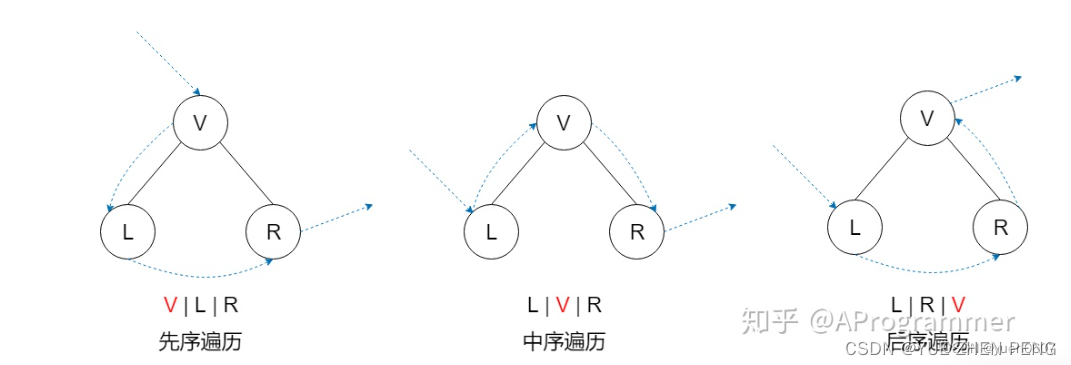
二叉树的前驱和后继是按中序遍历计算的,L称为前驱,R为后继。
- 如果一个树没有子节点,直接删除
- 如果一个树只有一个子节点,删除当前节点并把子节点补到这个位置
- 如果有两个子节点 ,操作复杂,进行以下操作
- 找到被删除的节点的左子树最大值或右子树最小值
- 我们选中右最小或者选中左最大
- 我们将这个选中的节点的子树连接在选中的节点的父节点
- 将选中节点替换到删除节点,并持有被删除节点的左右子树
//查找子树最大值
Node* FindMax(Node* node)
{
Node* current = node;
while(current!=nullptr)
{
current = current->right;
}
return current;
}
Node* FindMin(Node* node)
{
Node* current = node;
while(current!=nullptr)
{
current = current->left;
}
return current;
}
//需要先搜索找出被删除节点的指针
Node* DeleteNode(Node* root,Node* target)
{
//删除根节点,返回空指针
if(root==target)
{
return nullptr;
}
//子节点不存在,将当前节点从父节点上移除
if(target->left==nullptr&&target->right==nullptr)
{
target->parent = nullptr;
}
//一个子节点为空,左子节点为空
else if(target->left==nullptr)
{
if(target==target->parent->left)
{
target->parent->left = target->right;
target->right->parent = target->parent;
}
else
{
target->parent->right = target->right;
target->right->parent = target->parent;
}
}
else if(target->right==nullptr)
{
if(target==target->parent->right)
{
target->parent->right = target->left;
target->left->parent = target->parent;
}
else
{
target->parent->left = target->left;
target->left->parent = target->parent;
}
}
//两个子节点存在
else
{
//左侧最大,右侧最小值
Node* min = FindMin(target->right);
//选中的节点的子树连接在选中的节点的父节点
min->parent->left = min->left;
min->left->parent = min->parent;
min->parent->right= min->right;
min->right->parent = min->parent;
//选中节点置换删除节点
if(target->parent->left==target)
{
target->parent->left=min;
min->parent = target->parent;
}
else
{
target->parent->right = min;
min->parent = target->parent;
}
//选中节点继承被删除节点的子树
min->left = target->left;
target->left->parent = min;
min->right = target->right;
target->right->parent = min;
}
}
子树和相同树
递归实现的,可能存在爆栈风险,但是一般来讲BST的平均深度不会引起这种问题,可以使用。这里不再给出非递归实现
bool isSubtree(TreeNode* s, TreeNode* t) {
if (!s) return false; // 父树为空,不可能有子树
if (isSameTree(s, t)) return true; // 当前子树和子树t相同
return isSubtree(s->left, t) || isSubtree(s->right, t); // 继续递归检查左右子树
}
bool isSameTree(TreeNode* p, TreeNode* q) {
if (!p && !q) return true; // 两棵树都为空
if (!p || !q) return false; // 一棵树为空,另一棵不为空
return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
BST存在一个非常严重的问题,就是可能出现极端情况,这时BST会退化为一个双链表,导致丧失查找优势。