机械手是工业制造领域中应用最广泛的自动化机械设备,广泛应用于工业制造、医疗、军工、半导体制造、太空探索等领域。它们虽然形式不同,但都有一个共同的特点,即能够接受指令,并能准确定位到三维(或二维)空间的某一点进行工作。由于其在3D打印、喷漆机器人、汽车制造等领域的广泛应用,机器人的控制显得尤为重要。而滑模变结构控制SMC由于其快速的瞬态响应和对不确定性和扰动的鲁棒性,在机器人控制领域受到了广泛的关注。
问题描述
机器人轨迹跟踪控制问题可以描述为: 给定一个参考轨迹,找到一个容许控制u,使得实际的关节角度与参考的关节角度误差最小,从而使得机械臂末端轨迹跟踪上参考轨迹。
理论分析
1滑模控制基础概念
1.1滑模控制定义
滑模控制(SMC)也称为可变结构控制,本质上是一种特殊的非线性控制,其非线性性能是控制的不连续性。该控制策略与其他控制的区别在于“结构”系统的状态不是固定的,但是在动态过程中,它可以根据系统的当前状态(例如偏差和其导数)有意地进行更改,从而迫使系统以预定的“滑动模式”状态轨迹运动。滑模的设计可以不受对象参数和干扰的影响,滑模控制具有响应速度快,对参数变化和干扰不敏感,无需在线系统识别,物理实现简单等优点。通过不连续控制有意改变系统结构将相位轨迹驱动到稳定的超平面或流形的系统。不受干扰和参数变化
1.2滑模趋近律
滑模控制下的系统一般分为两个阶段:
(1)从系统初始状态到滑模面;
(2)在滑模面上滑模到达系统平衡点;
2.将趋近律引入到(1)阶段设计中,对(2)阶段设计快速终端滑模。2.“全局”、“快速”、“终端滑模”中的“全局”表示滑模没有(1)阶段,因此不使用趋近定律。
4个基本趋近律表达如下:
(1)等速趋近律:
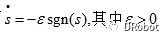
(2)指数趋近律
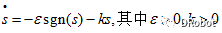
(3)幂次趋近律

(4)一般趋近律
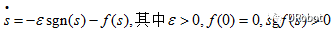
3基于指数趋近律的模糊滑模控制
3.1 基于指数趋近律的滑模控制
由牛顿欧拉公式得n自由度机器人关节空间动力学方程为:
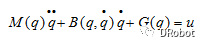
设系统误差为:
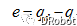
则误差的微分得:
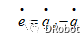
选择滑模函数为:
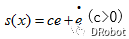
则对滑模函数s求导得:
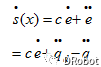
因为系统方程可变形为:
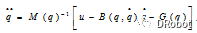
所以:

选取指数趋近律为:
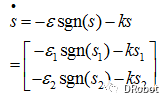
所以基于指数趋近律可设计u,将两公式合并:
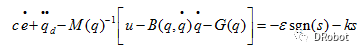
则控制律u为:

已知只要得到滑模平面(切换面s)和滑动模态的控制律u,滑动变结构控制就能完全建立起来。
下面证明其滑模平面稳定存在滑动模态:
第一步:取李雅普诺夫函数
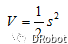
由于
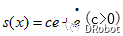
所以V是正定(PD)
第二步:对李雅普诺夫函数求导得:

由此可知,上述设计的滑模变结构控制器满足要求。
为更直观的分析所设计的滑模控制器的优劣,对控制系统进行仿真分析如下:
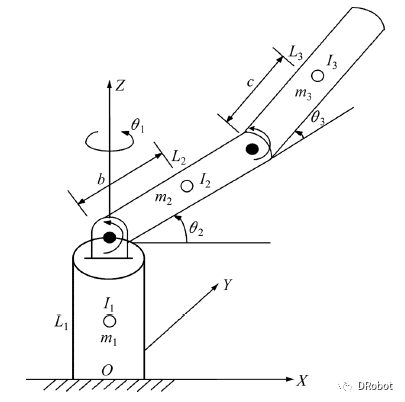
图1.三自由度机械臂
根据拉格朗日功能平衡法,建立其动力学模型。由于是比较常见的三自由度机器人模型,这里可以查找教科书或文献参考
MATLAB仿真程序
其simulink建模框图如图2所示:
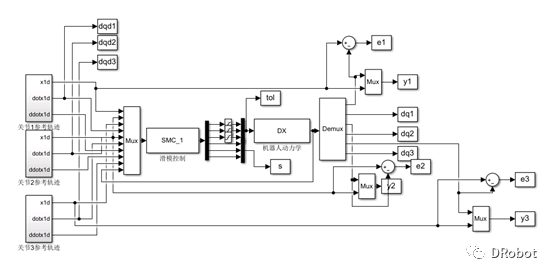
图2 控制系统simulink框图
机器人动力学MATLAB仿真程序:
function [sys,x0,str,ts]=s_function(t,x,u,flag)switch flag,case 0,[sys,x0,str,ts]=mdlInitializeSizes;case 1,sys=mdlDerivatives(t,x,u);case 3,sys=mdlOutputs(t,x,u);case {2, 4, 9 }sys = [];otherwiseerror(['Unhandled flag = ',num2str(flag)]);endfunction [sys,x0,str,ts]=mdlInitializeSizessizes = simsizes;sizes.NumContStates = 6;sizes.NumDiscStates = 0;sizes.NumOutputs = 6;sizes.NumInputs = 3;sizes.DirFeedthrough = 0;sizes.NumSampleTimes = 0;sys=simsizes(sizes);x0=[0.6;0.3;0.5;0.5;0.5;0.5];str=[];ts=[];function sys=mdlDerivatives(t,x,u)q1=x(1);dq1=x(2);q2=x(3);dq2=x(4);q3=x(5);dq3=x(6);m1=0;m2=1;m3=1;L1=0;L2=1;L3=1;g=10;I1=0;I2=0;I3=0;a1=m2*L2^2+m3*L2^2;a2=m3*L3^2;a3=m3*L3^2;b1=(m2*L2+m3*L2)*g;b2=m3*L3*g;M11=I1+a1*(cos(q2))^2+a2*cos(q2+q3)+2*a2*cos(q2)*cos(q2+q3);M12=0;M13=0;M21=0;M22=I2+a1+a2+2*a3*cos(q3);M23=a2+a3*cos(q3);M31=0;M32=a2+a3*cos(q3);M33=I3+a2;M=[M11 M12 M13;M21 M22 M23;M31 M32 M33];B11=-(1/2)*a1*dq2*sin(2*q2)-a3*dq3*cos(q2)*sin(q2+q3)-(1/2)*a2*(dq2+dq3)*sin(2*q2+2*q3)-a3*dq2*sin(2*q2+q3);B12=-(1/2)*a1*dq1*sin(2*q2)-a3*dq1*sin(2*q2+q3)-(1/2)*a2*dq1*sin(2*q2+2*q3);B13=-a3*dq1*cos(q2)*sin(q2+q3)-(1/2)*a1*dq1*sin(2*q2+2*q3);B21=-B12;B22=-a3*dq3*sin(q3);B23=-a3*(dq2+dq3)*sin(q3);B31=-B13;B32=-a3*dq2*sin(q3);B33=0;B=[B11 B12 B13;B21 B22 B23;B31 B32 B33];G1=0;G2=b1*cos(q2)+b2*cos(q2+q3);G3=b2*cos(q2+q3);G=[G1;G2;G3];tol(1)=u(1);tol(2)=u(2);tol(3)=u(3);ddq=inv(M)*(tol'-B*[dq1;dq2;dq3]-G);sys(1)=x(2);sys(2)=ddq(1);sys(3)=x(4);sys(4)=ddq(2);sys(5)=x(6);sys(6)=ddq(3);function sys=mdlOutputs(t,x,u)sys(1)=x(1);sys(2)=x(2);sys(3)=x(3);sys(4)=x(4);sys(5)=x(5);sys(6)=x(6);
则各关节跟踪响应如图3所示

图3.各关节跟踪响应
轨迹跟踪误差如图4所示

图4.轨迹跟踪误差
滑模面如图5所示
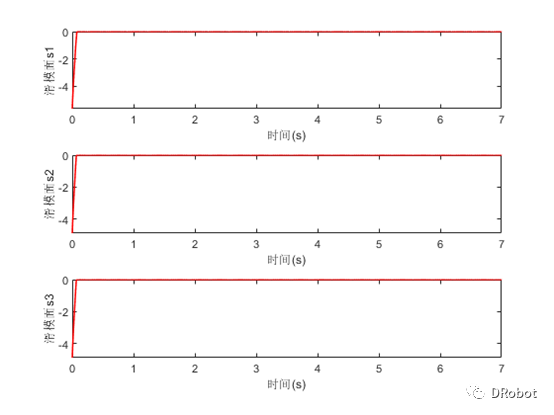
图5.滑模面
控制力矩如图6所示
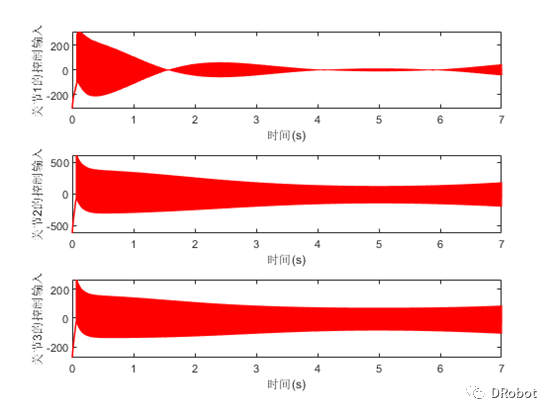
图6.控制力矩
总结
由以上仿真结果可以看出,基于趋近律的滑模轨迹跟踪控制器在系统复杂的环境下,能够对系统的轨迹跟踪进行有效的控制,然而,其基于趋近律的滑模轨迹跟踪控制方法存在着严重的抖振,还是有待改进!
更多信息请关注:DRobot

![[NewStarCTF 2023 公开赛道] week1 Crypto](https://img-blog.csdnimg.cn/6e6aba16652347f2881a2605a48caf6b.png)