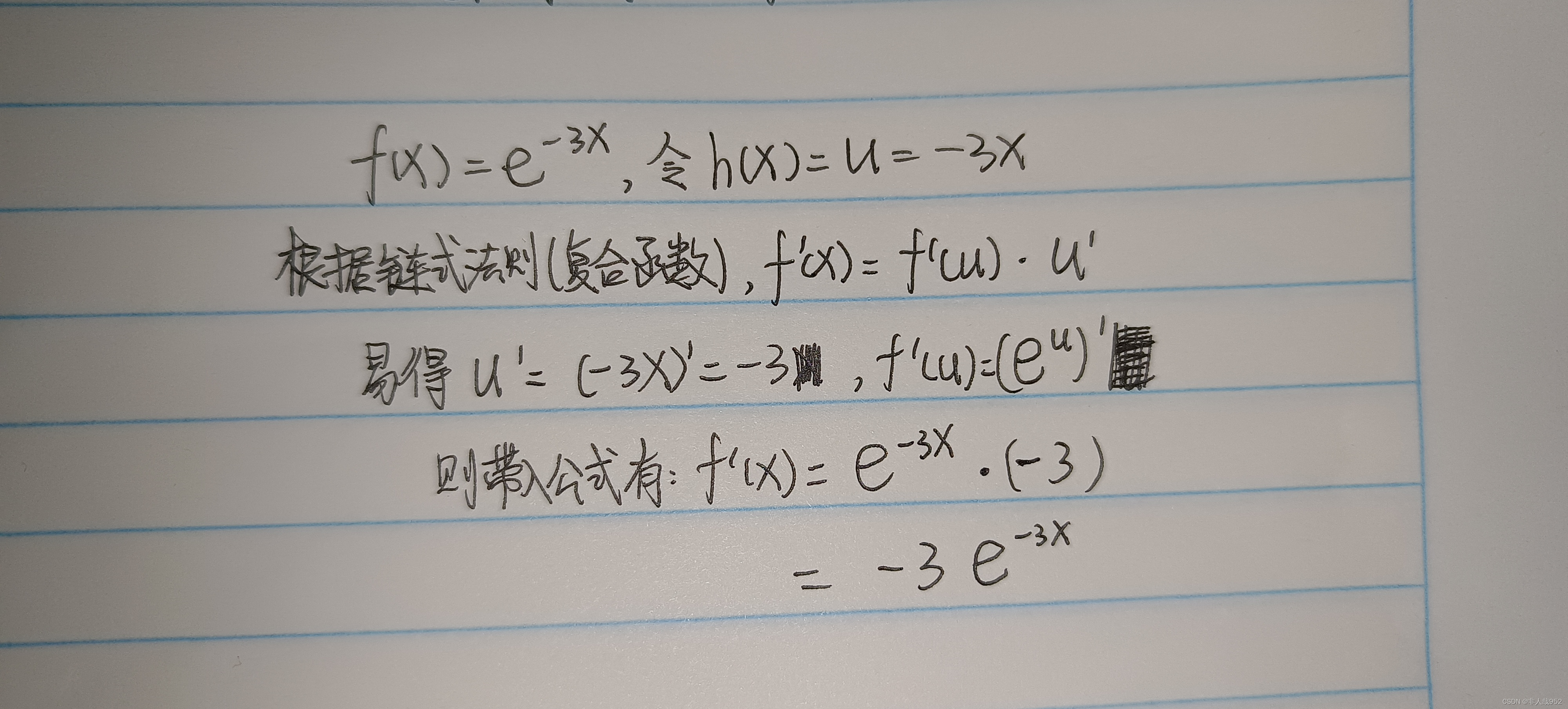一、直接公式法

对于指数函数 f(x) = e^g(x)，其中 g(x) 是关于 x 的函数，导数 f'(x) 可以表示为 f'(x) = g'(x) * e^g(x)。

在我们的情况下，g(x) = -3x。

我们先求导 g'(x) = （-3x）'= -3。因此，我们有 g'(x) = -3。

现在，我们将 g'(x) 和 e^g(x) 带入导数公式 f'(x) = g'(x) * e^g(x)。

f'(x) = (-3) * e^(-x)
       = -3e^(-x)

这样是一种写法举例:
 

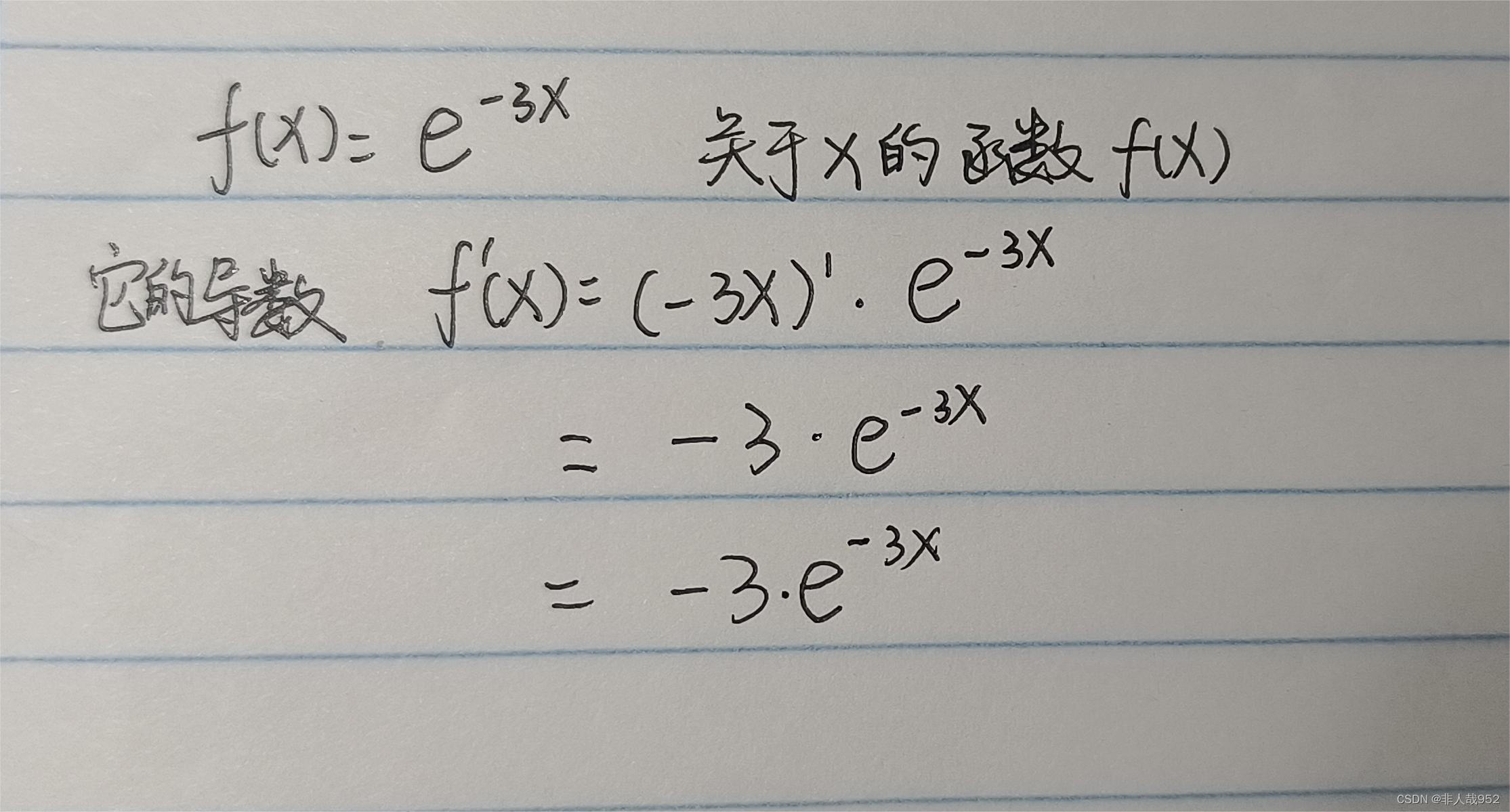
二、复合函数 思路法:

当我们需要求导一个复合函数时，可以使用链式法则。

我们的函数 f(x) = e^(-3x) 可以表示为 g(h(x)) 的形式，其中 g(u) = e^u，h(x) =u= -3x。

根据链式法则，导数 f'(x) 可以表示为 g'(h(x)) * h'(x) 就是  g'(u) * u'   (1)。

我们先求导 g(u) = e^u。

指数函数 e^u 的导数是它本身(把u看作整体)，即 g'(u) = e^u    (2)。

接下来，我们求导 h'(x)=u'= =（-3x)'= -3   （3）。常数乘法法则告诉我们，导数 h'(x)即u'= -3。

现在，我们将 g'(u) 和 u 带入导数公式 f'(x) = g'(u) * u'。

f'(x) = g'(u) * u'
       = e^(-3x) * (-3x)'
       = -e^(-3x)* (-3)=-3*e^(-3x)

接下来我举例一种写法: